Learning Neural Eigenfunctions for Unsupervised Semantic Segmentation

Unsupervised semantic segmentation is a long-standing challenge in computer vision with great significance. Spectral clustering is a theoretically grounded solution to it where the spectral embeddings for pixels are computed to construct distinct clusters. Despite recent progress in enhancing spectral clustering with powerful pre-trained models, current approaches still suffer from inefficiencies in spectral decomposition and inflexibility in applying them to the test data. This work addresses these issues by casting spectral clustering as a parametric approach that employs neural network-based eigenfunctions to produce spectral embeddings. The outputs of the neural eigenfunctions are further restricted to discrete vectors that indicate clustering assignments directly. As a result, an end-to-end NN-based paradigm of spectral clustering emerges. In practice, the neural eigenfunctions are lightweight and take the features from pre-trained models as inputs, improving training efficiency and unleashing the potential of pre-trained models for dense prediction. We conduct extensive empirical studies to validate the effectiveness of our approach and observe significant performance gains over competitive baselines on Pascal Context, Cityscapes, and ADE20K benchmarks.

Iterative Teaching by Data Hallucination

We consider the problem of iterative machine teaching, where a teacher sequentially provides examples based on the status of a learner under a discrete input space (i.e., a pool of finite samples), which greatly limits the teacher's capability. To address this issue, we study iterative teaching under a continuous input space where the input example (i.e., image) can be either generated by solving an optimization problem or drawn directly from a continuous distribution. Specifically, we propose data hallucination teaching (DHT) where the teacher can generate input data intelligently based on labels, the learner's status and the target concept. We study a number of challenging teaching setups (e.g., linear/neural learners in omniscient and black-box settings). Extensive empirical results verify the effectiveness of DHT.

Spectral Representation Learning for Conditional Moment Models

Many problems in causal inference and economics can be formulated in the framework of conditional moment models, which characterize the target function through a collection of conditional moment restrictions. For nonparametric conditional moment models, efficient estimation has always relied on preimposed conditions on various measures of ill-posedness of the hypothesis space, which are hard to validate when flexible models are used. In this work, we address this issue by proposing a procedure that automatically learns representations with controlled measures of ill-posedness. Our method approximates a linear representation defined by the spectral decomposition of a conditional expectation operator, which can be used for kernelized estimators and is known to facilitate minimax optimal estimation in certain settings. We show this representation can be efficiently estimated from data, and establish L2 consistency for the resulting estimator. We evaluate the proposed method on proximal causal inference tasks, exhibiting promising performance on high-dimensional, semi-synthetic data.

Learning Counterfactually Invariant Predictors

We propose a method to learn predictors that are invariant under counterfactual changes of certain covariates. This method is useful when the prediction target is causally influenced by covariates that should not affect the predictor output. For instance, an object recognition model may be influenced by position, orientation, or scale of the object itself. We address the problem of training predictors that are explicitly counterfactually invariant to changes of such covariates. We propose a model-agnostic regularization term based on conditional kernel mean embeddings, to enforce counterfactual invariance during training. We prove the soundness of our method, which can handle mixed categorical and continuous multi-variate attributes. Empirical results on synthetic and real-world data demonstrate the efficacy of our method in a variety of settings.

SUMO: Unbiased Estimation of Log Marginal Probability for Latent Variable Models

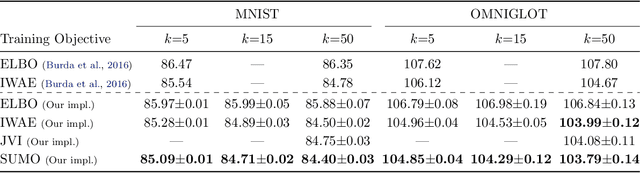
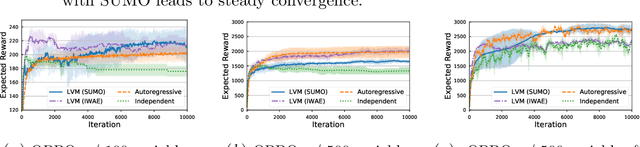
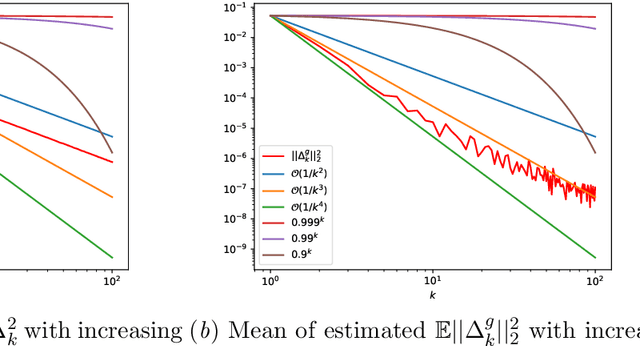
Standard variational lower bounds used to train latent variable models produce biased estimates of most quantities of interest. We introduce an unbiased estimator of the log marginal likelihood and its gradients for latent variable models based on randomized truncation of infinite series. If parameterized by an encoder-decoder architecture, the parameters of the encoder can be optimized to minimize its variance of this estimator. We show that models trained using our estimator give better test-set likelihoods than a standard importance-sampling based approach for the same average computational cost. This estimator also allows use of latent variable models for tasks where unbiased estimators, rather than marginal likelihood lower bounds, are preferred, such as minimizing reverse KL divergences and estimating score functions.

DBSN: Measuring Uncertainty through Bayesian Learning of Deep Neural Network Structures

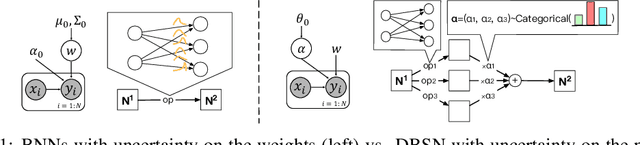
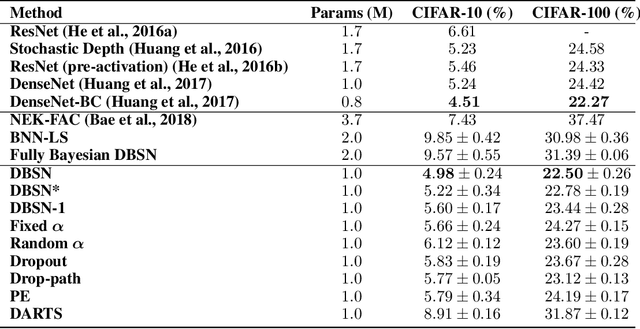
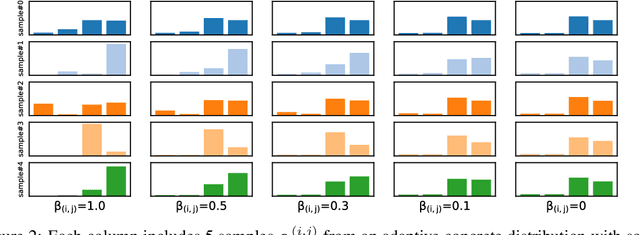
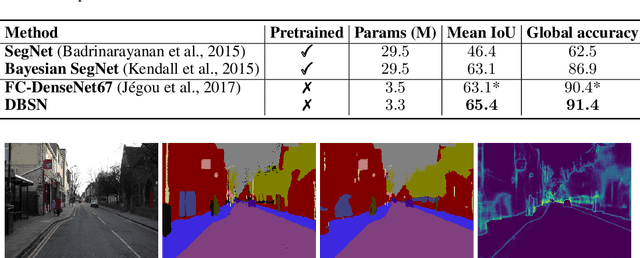
Bayesian neural networks (BNNs) introduce uncertainty estimation to deep networks by performing Bayesian inference on network weights. However, such models bring the challenges of inference, and further BNNs with weight uncertainty rarely achieve superior performance to standard models. In this paper, we investigate a new line of Bayesian deep learning by performing Bayesian reasoning on the structure of deep neural networks. Drawing inspiration from the neural architecture search, we define the network structure as gating weights on the redundant operations between computational nodes, and apply stochastic variational inference techniques to learn the structure distributions of networks. Empirically, the proposed method substantially surpasses the advanced deep neural networks across a range of classification and segmentation tasks. More importantly, our approach also preserves benefits of Bayesian principles, producing improved uncertainty estimation than the strong baselines including MC dropout and variational BNNs algorithms (e.g. noisy EK-FAC).

A Simple yet Effective Baseline for Robust Deep Learning with Noisy Labels

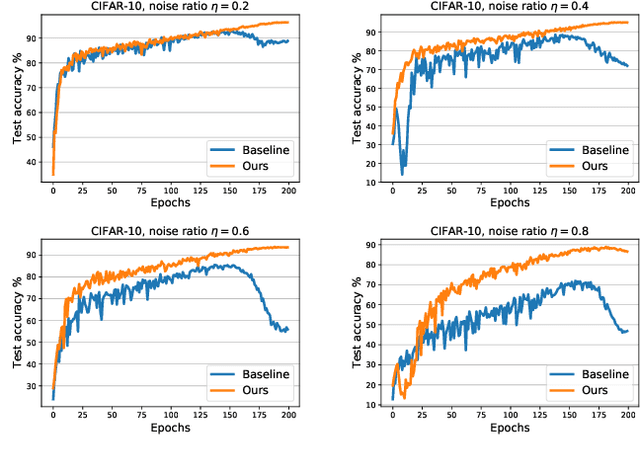
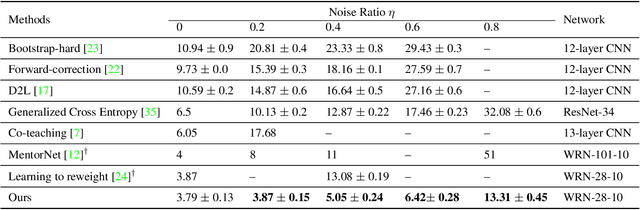
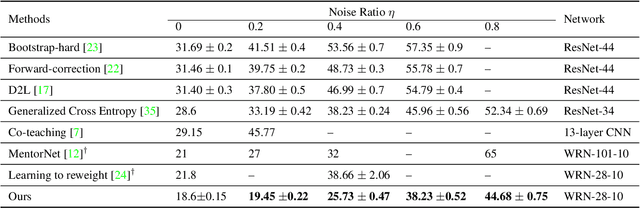
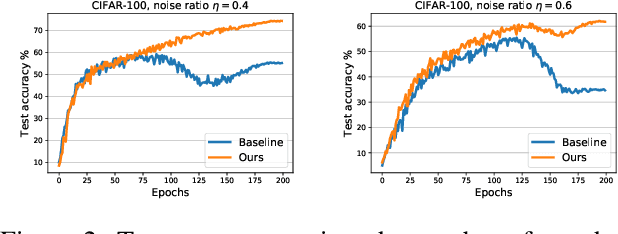
Recently deep neural networks have shown their capacity to memorize training data, even with noisy labels, which hurts generalization performance. To mitigate this issue, we provide a simple but effective baseline method that is robust to noisy labels, even with severe noise. Our objective involves a variance regularization term that implicitly penalizes the Jacobian norm of the neural network on the whole training set (including the noisy-labeled data), which encourages generalization and prevents overfitting to the corrupted labels. Experiments on both synthetically generated incorrect labels and realistic large-scale noisy datasets demonstrate that our approach achieves state-of-the-art performance with a high tolerance to severe noise.

Cluster Alignment with a Teacher for Unsupervised Domain Adaptation

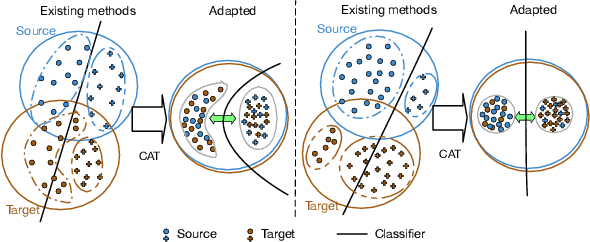
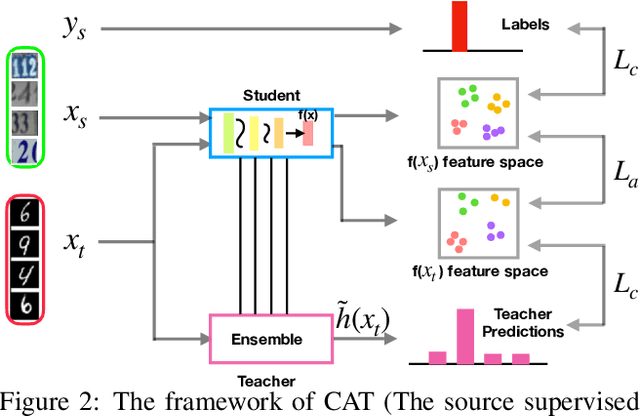
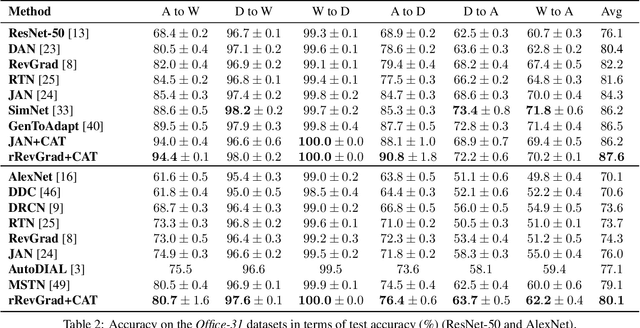
Deep learning methods have shown promise in unsupervised domain adaptation, which aims to leverage a labeled source domain to learn a classifier for the unlabeled target domain with a different distribution. However, such methods typically learn a domain-invariant representation space to match the marginal distributions of the source and target domains, while ignoring their fine-level structures. In this paper, we propose Cluster Alignment with a Teacher (CAT) for unsupervised domain adaptation, which can effectively incorporate the discriminative clustering structures in both domains for better adaptation. Technically, CAT leverages an implicit ensembling teacher model to reliably discover the class-conditional structure in the feature space for the unlabeled target domain. Then CAT forces the features of both the source and the target domains to form discriminative class-conditional clusters and aligns the corresponding clusters across domains. Empirical results demonstrate that CAT achieves state-of-the-art results in several unsupervised domain adaptation scenarios.

Semi-crowdsourced Clustering with Deep Generative Models

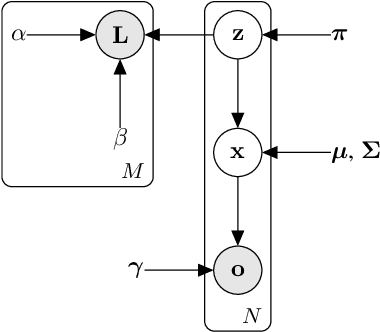
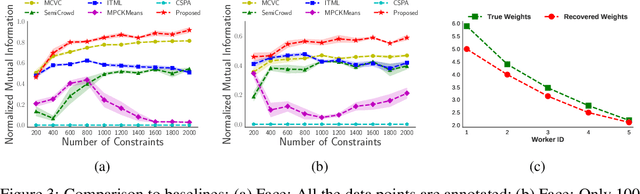
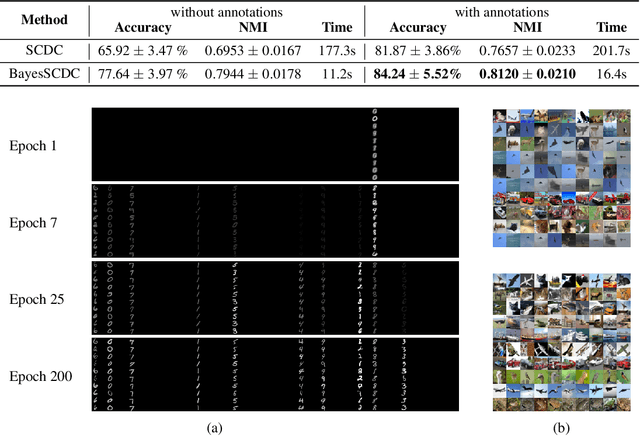
We consider the semi-supervised clustering problem where crowdsourcing provides noisy information about the pairwise comparisons on a small subset of data, i.e., whether a sample pair is in the same cluster. We propose a new approach that includes a deep generative model (DGM) to characterize low-level features of the data, and a statistical relational model for noisy pairwise annotations on its subset. The two parts share the latent variables. To make the model automatically trade-off between its complexity and fitting data, we also develop its fully Bayesian variant. The challenge of inference is addressed by fast (natural-gradient) stochastic variational inference algorithms, where we effectively combine variational message passing for the relational part and amortized learning of the DGM under a unified framework. Empirical results on synthetic and real-world datasets show that our model outperforms previous crowdsourced clustering methods.

Smooth Neighbors on Teacher Graphs for Semi-supervised Learning

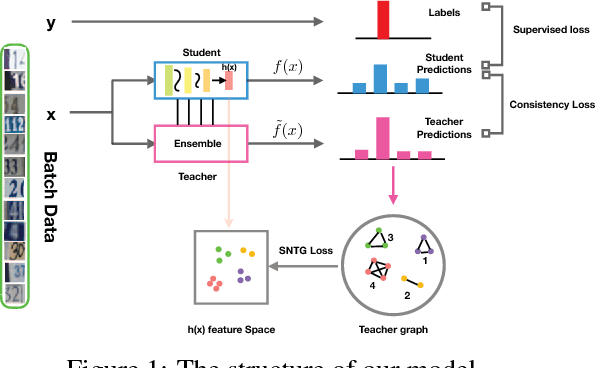
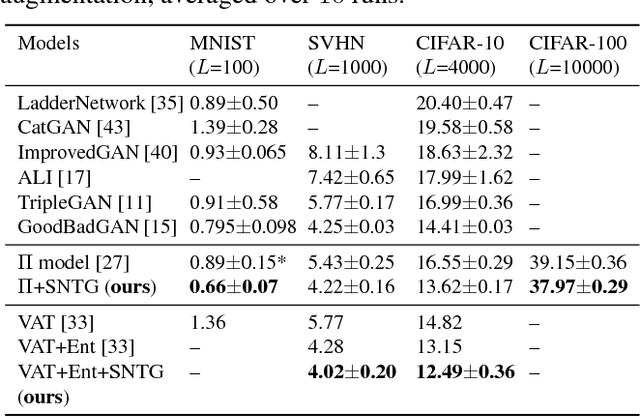
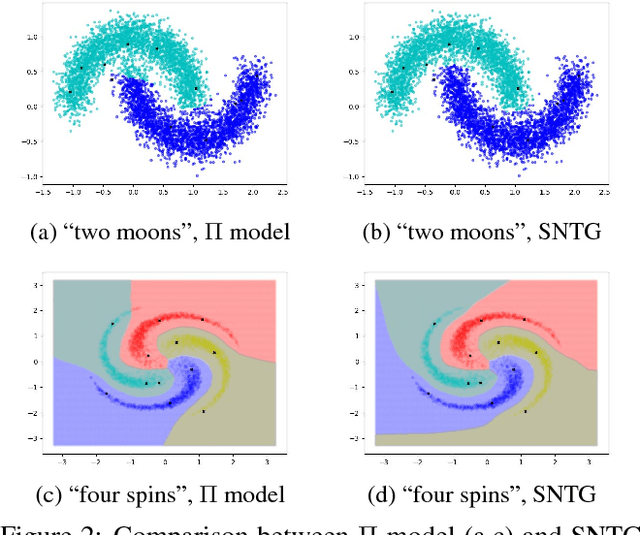
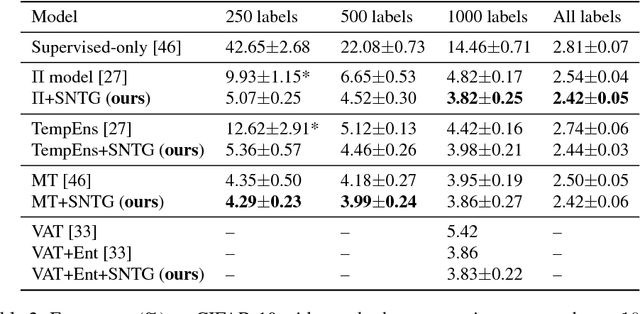
The recently proposed self-ensembling methods have achieved promising results in deep semi-supervised learning, which penalize inconsistent predictions of unlabeled data under different perturbations. However, they only consider adding perturbations to each single data point, while ignoring the connections between data samples. In this paper, we propose a novel method, called Smooth Neighbors on Teacher Graphs (SNTG). In SNTG, a graph is constructed based on the predictions of the teacher model, i.e., the implicit self-ensemble of models. Then the graph serves as a similarity measure with respect to which the representations of "similar" neighboring points are learned to be smooth on the low-dimensional manifold. We achieve state-of-the-art results on semi-supervised learning benchmarks. The error rates are 9.89%, 3.99% for CIFAR-10 with 4000 labels, SVHN with 500 labels, respectively. In particular, the improvements are significant when the labels are fewer. For the non-augmented MNIST with only 20 labels, the error rate is reduced from previous 4.81% to 1.36%. Our method also shows robustness to noisy labels.