Meta-PDE: Learning to Solve PDEs Quickly Without a Mesh

Partial differential equations (PDEs) are often computationally challenging to solve, and in many settings many related PDEs must be be solved either at every timestep or for a variety of candidate boundary conditions, parameters, or geometric domains. We present a meta-learning based method which learns to rapidly solve problems from a distribution of related PDEs. We use meta-learning (MAML and LEAP) to identify initializations for a neural network representation of the PDE solution such that a residual of the PDE can be quickly minimized on a novel task. We apply our meta-solving approach to a nonlinear Poisson's equation, 1D Burgers' equation, and hyperelasticity equations with varying parameters, geometries, and boundary conditions. The resulting Meta-PDE method finds qualitatively accurate solutions to most problems within a few gradient steps; for the nonlinear Poisson and hyper-elasticity equation this results in an intermediate accuracy approximation up to an order of magnitude faster than a baseline finite element analysis (FEA) solver with equivalent accuracy. In comparison to other learned solvers and surrogate models, this meta-learning approach can be trained without supervision from expensive ground-truth data, does not require a mesh, and can even be used when the geometry and topology varies between tasks.

Randomized Automatic Differentiation

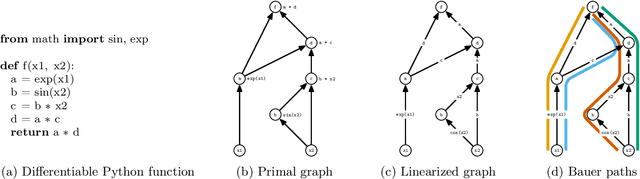
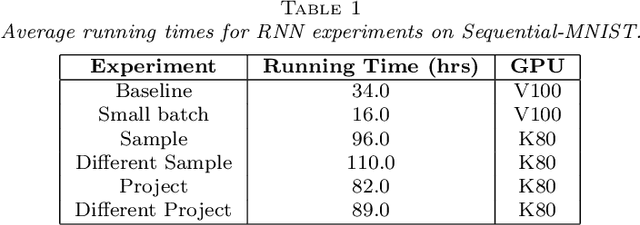
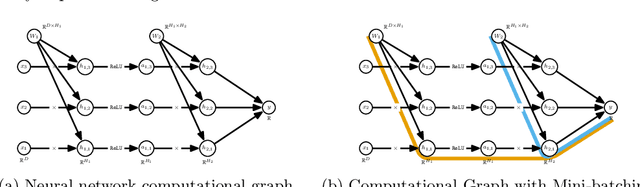
The successes of deep learning, variational inference, and many other fields have been aided by specialized implementations of reverse-mode automatic differentiation (AD) to compute gradients of mega-dimensional objectives. The AD techniques underlying these tools were designed to compute exact gradients to numerical precision, but modern machine learning models are almost always trained with stochastic gradient descent. Why spend computation and memory on exact (minibatch) gradients only to use them for stochastic optimization? We develop a general framework and approach for randomized automatic differentiation (RAD), which allows unbiased gradient estimates to be computed with reduced memory in return for variance. We examine limitations of the general approach, and argue that we must leverage problem specific structure to realize benefits. We develop RAD techniques for a variety of simple neural network architectures, and show that for a fixed memory budget, RAD converges in fewer iterations than using a small batch size for feedforward networks, and in a similar number for recurrent networks. We also show that RAD can be applied to scientific computing, and use it to develop a low-memory stochastic gradient method for optimizing the control parameters of a linear reaction-diffusion PDE representing a fission reactor.

Learning Composable Energy Surrogates for PDE Order Reduction

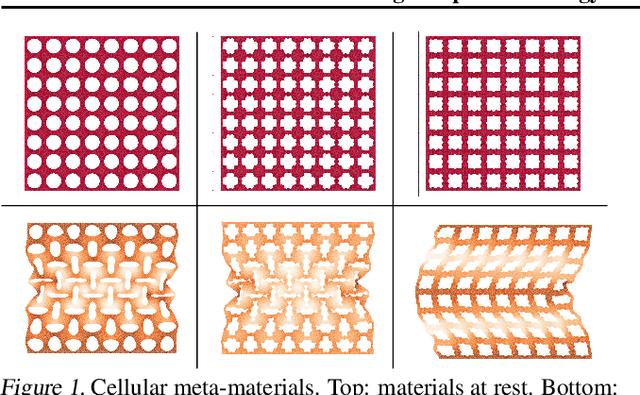
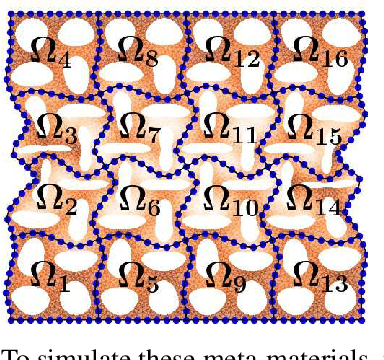
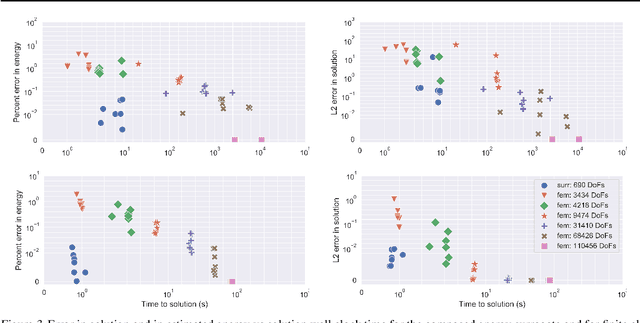
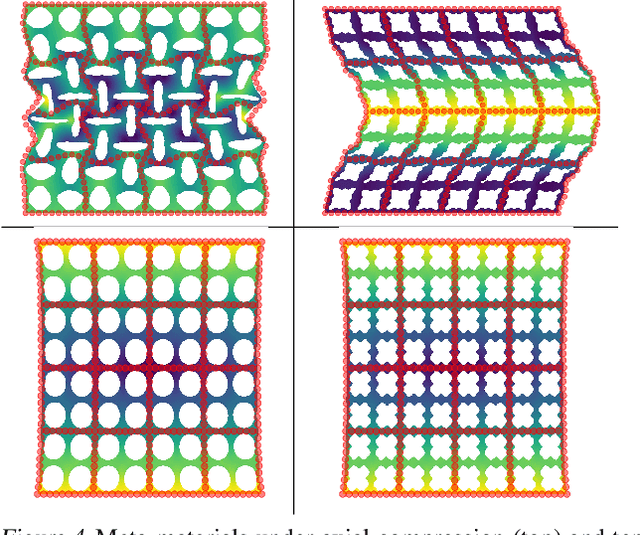
Meta-materials are an important emerging class of engineered materials in which complex macroscopic behaviour--whether electromagnetic, thermal, or mechanical--arises from modular substructure. Simulation and optimization of these materials are computationally challenging, as rich substructures necessitate high-fidelity finite element meshes to solve the governing PDEs. To address this, we leverage parametric modular structure to learn component-level surrogates, enabling cheaper high-fidelity simulation. We use a neural network to model the stored potential energy in a component given boundary conditions. This yields a structured prediction task: macroscopic behavior is determined by the minimizer of the system's total potential energy, which can be approximated by composing these surrogate models. Composable energy surrogates thus permit simulation in the reduced basis of component boundaries. Costly ground-truth simulation of the full structure is avoided, as training data are generated by performing finite element analysis with individual components. Using dataset aggregation to choose training boundary conditions allows us to learn energy surrogates which produce accurate macroscopic behavior when composed, accelerating simulation of parametric meta-materials.

SUMO: Unbiased Estimation of Log Marginal Probability for Latent Variable Models

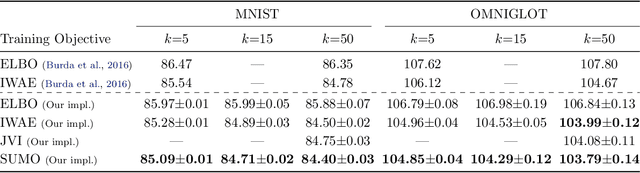
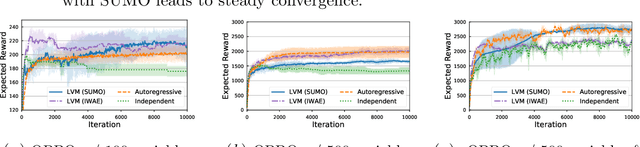
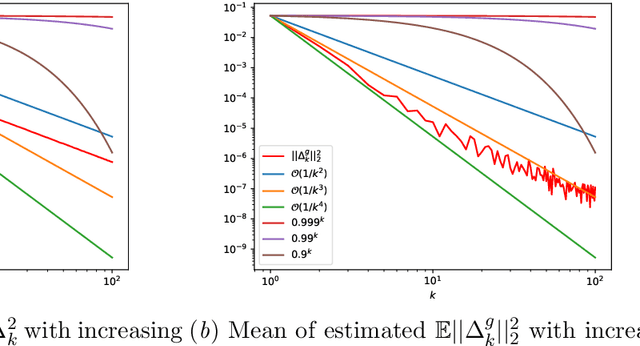
Standard variational lower bounds used to train latent variable models produce biased estimates of most quantities of interest. We introduce an unbiased estimator of the log marginal likelihood and its gradients for latent variable models based on randomized truncation of infinite series. If parameterized by an encoder-decoder architecture, the parameters of the encoder can be optimized to minimize its variance of this estimator. We show that models trained using our estimator give better test-set likelihoods than a standard importance-sampling based approach for the same average computational cost. This estimator also allows use of latent variable models for tasks where unbiased estimators, rather than marginal likelihood lower bounds, are preferred, such as minimizing reverse KL divergences and estimating score functions.

Efficient Optimization of Loops and Limits with Randomized Telescoping Sums

We consider optimization problems in which the objective requires an inner loop with many steps or is the limit of a sequence of increasingly costly approximations. Meta-learning, training recurrent neural networks, and optimization of the solutions to differential equations are all examples of optimization problems with this character. In such problems, it can be expensive to compute the objective function value and its gradient, but truncating the loop or using less accurate approximations can induce biases that damage the overall solution. We propose randomized telescope (RT) gradient estimators, which represent the objective as the sum of a telescoping series and sample linear combinations of terms to provide cheap unbiased gradient estimates. We identify conditions under which RT estimators achieve optimization convergence rates independent of the length of the loop or the required accuracy of the approximation. We also derive a method for tuning RT estimators online to maximize a lower bound on the expected decrease in loss per unit of computation. We evaluate our adaptive RT estimators on a range of applications including meta-optimization of learning rates, variational inference of ODE parameters, and training an LSTM to model long sequences.

Continual Learning in Generative Adversarial Nets

Developments in deep generative models have allowed for tractable learning of high-dimensional data distributions. While the employed learning procedures typically assume that training data is drawn i.i.d. from the distribution of interest, it may be desirable to model distinct distributions which are observed sequentially, such as when different classes are encountered over time. Although conditional variations of deep generative models permit multiple distributions to be modeled by a single network in a disentangled fashion, they are susceptible to catastrophic forgetting when the distributions are encountered sequentially. In this paper, we adapt recent work in reducing catastrophic forgetting to the task of training generative adversarial networks on a sequence of distinct distributions, enabling continual generative modeling.