Graph Neural Networks Gone Hogwild

Message passing graph neural networks (GNNs) would appear to be powerful tools to learn distributed algorithms via gradient descent, but generate catastrophically incorrect predictions when nodes update asynchronously during inference. This failure under asynchrony effectively excludes these architectures from many potential applications, such as learning local communication policies between resource-constrained agents in, e.g., robotic swarms or sensor networks. In this work we explore why this failure occurs in common GNN architectures, and identify "implicitly-defined" GNNs as a class of architectures which is provably robust to partially asynchronous "hogwild" inference, adapting convergence guarantees from work in asynchronous and distributed optimization, e.g., Bertsekas (1982); Niu et al. (2011). We then propose a novel implicitly-defined GNN architecture, which we call an energy GNN. We show that this architecture outperforms other GNNs from this class on a variety of synthetic tasks inspired by multi-agent systems, and achieves competitive performance on real-world datasets.

Neuromechanical Autoencoders: Learning to Couple Elastic and Neural Network Nonlinearity

Intelligent biological systems are characterized by their embodiment in a complex environment and the intimate interplay between their nervous systems and the nonlinear mechanical properties of their bodies. This coordination, in which the dynamics of the motor system co-evolved to reduce the computational burden on the brain, is referred to as ``mechanical intelligence'' or ``morphological computation''. In this work, we seek to develop machine learning analogs of this process, in which we jointly learn the morphology of complex nonlinear elastic solids along with a deep neural network to control it. By using a specialized differentiable simulator of elastic mechanics coupled to conventional deep learning architectures -- which we refer to as neuromechanical autoencoders -- we are able to learn to perform morphological computation via gradient descent. Key to our approach is the use of mechanical metamaterials -- cellular solids, in particular -- as the morphological substrate. Just as deep neural networks provide flexible and massively-parametric function approximators for perceptual and control tasks, cellular solid metamaterials are promising as a rich and learnable space for approximating a variety of actuation tasks. In this work we take advantage of these complementary computational concepts to co-design materials and neural network controls to achieve nonintuitive mechanical behavior. We demonstrate in simulation how it is possible to achieve translation, rotation, and shape matching, as well as a ``digital MNIST'' task. We additionally manufacture and evaluate one of the designs to verify its real-world behavior.

Meta-PDE: Learning to Solve PDEs Quickly Without a Mesh

Partial differential equations (PDEs) are often computationally challenging to solve, and in many settings many related PDEs must be be solved either at every timestep or for a variety of candidate boundary conditions, parameters, or geometric domains. We present a meta-learning based method which learns to rapidly solve problems from a distribution of related PDEs. We use meta-learning (MAML and LEAP) to identify initializations for a neural network representation of the PDE solution such that a residual of the PDE can be quickly minimized on a novel task. We apply our meta-solving approach to a nonlinear Poisson's equation, 1D Burgers' equation, and hyperelasticity equations with varying parameters, geometries, and boundary conditions. The resulting Meta-PDE method finds qualitatively accurate solutions to most problems within a few gradient steps; for the nonlinear Poisson and hyper-elasticity equation this results in an intermediate accuracy approximation up to an order of magnitude faster than a baseline finite element analysis (FEA) solver with equivalent accuracy. In comparison to other learned solvers and surrogate models, this meta-learning approach can be trained without supervision from expensive ground-truth data, does not require a mesh, and can even be used when the geometry and topology varies between tasks.

Randomized Automatic Differentiation

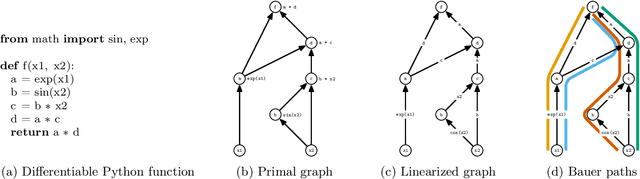
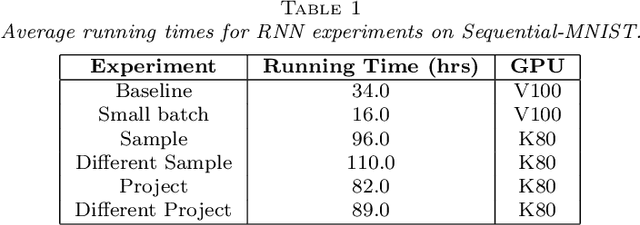
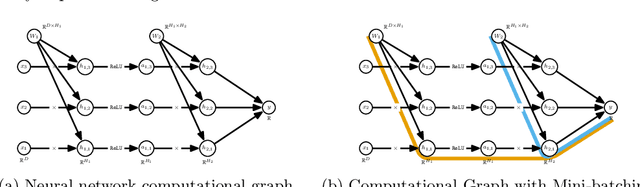
The successes of deep learning, variational inference, and many other fields have been aided by specialized implementations of reverse-mode automatic differentiation (AD) to compute gradients of mega-dimensional objectives. The AD techniques underlying these tools were designed to compute exact gradients to numerical precision, but modern machine learning models are almost always trained with stochastic gradient descent. Why spend computation and memory on exact (minibatch) gradients only to use them for stochastic optimization? We develop a general framework and approach for randomized automatic differentiation (RAD), which allows unbiased gradient estimates to be computed with reduced memory in return for variance. We examine limitations of the general approach, and argue that we must leverage problem specific structure to realize benefits. We develop RAD techniques for a variety of simple neural network architectures, and show that for a fixed memory budget, RAD converges in fewer iterations than using a small batch size for feedforward networks, and in a similar number for recurrent networks. We also show that RAD can be applied to scientific computing, and use it to develop a low-memory stochastic gradient method for optimizing the control parameters of a linear reaction-diffusion PDE representing a fission reactor.

On Predictive Information Sub-optimality of RNNs

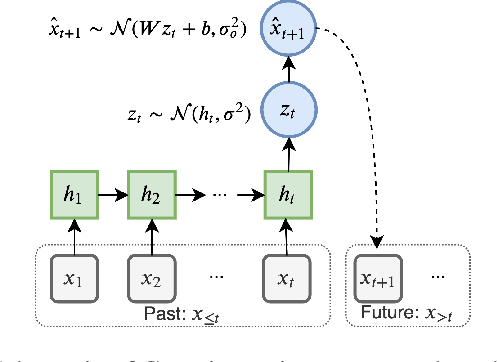
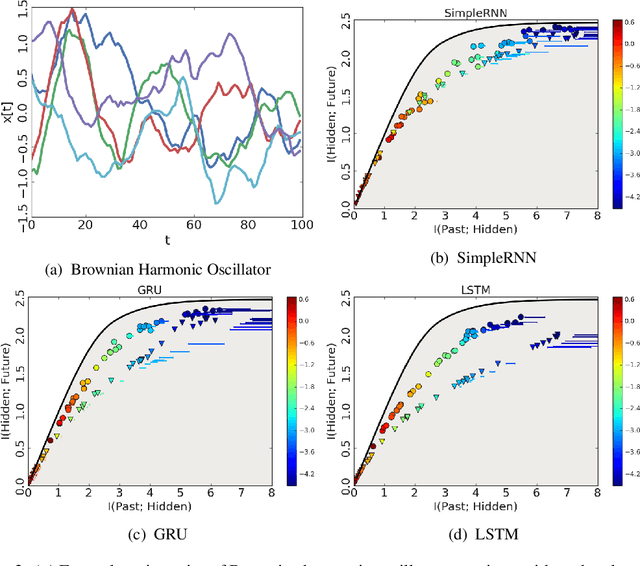
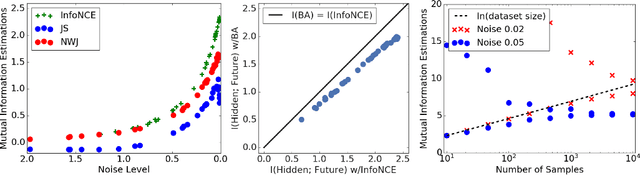
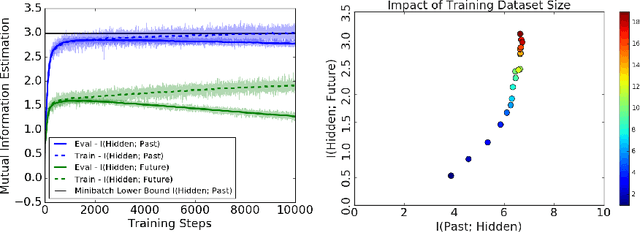
Certain biological neurons demonstrate a remarkable capability to optimally compress the history of sensory inputs while being maximally informative about the future. In this work, we investigate if the same can be said of artificial neurons in recurrent neural networks (RNNs) trained with maximum likelihood. In experiments on two datasets, restorative Brownian motion and a hand-drawn sketch dataset, we find that RNNs are sub-optimal in the information plane. Instead of optimally compressing past information, they extract additional information that is not relevant for predicting the future. Overcoming this limitation may require alternative training procedures and architectures, or objectives beyond maximum likelihood estimation.

Model Compression by Entropy Penalized Reparameterization

We describe an end-to-end neural network weight compression approach that draws inspiration from recent latent-variable data compression methods. The network parameters (weights and biases) are represented in a "latent" space, amounting to a reparameterization. This space is equipped with a learned probability model, which is used to impose an entropy penalty on the parameter representation during training, and to compress the representation using arithmetic coding after training. We are thus maximizing accuracy and model compressibility jointly, in an end-to-end fashion, with the rate--error trade-off specified by a hyperparameter. We evaluate our method by compressing six distinct model architectures on the MNIST, CIFAR-10 and ImageNet classification benchmarks. Our method achieves state-of-the-art compression on VGG-16, LeNet300-100 and several ResNet architectures, and is competitive on LeNet-5.

Predicting Motivations of Actions by Leveraging Text

Understanding human actions is a key problem in computer vision. However, recognizing actions is only the first step of understanding what a person is doing. In this paper, we introduce the problem of predicting why a person has performed an action in images. This problem has many applications in human activity understanding, such as anticipating or explaining an action. To study this problem, we introduce a new dataset of people performing actions annotated with likely motivations. However, the information in an image alone may not be sufficient to automatically solve this task. Since humans can rely on their lifetime of experiences to infer motivation, we propose to give computer vision systems access to some of these experiences by using recently developed natural language models to mine knowledge stored in massive amounts of text. While we are still far away from fully understanding motivation, our results suggest that transferring knowledge from language into vision can help machines understand why people in images might be performing an action.