Distributional Equivalence and Structure Learning for Bow-free Acyclic Path Diagrams

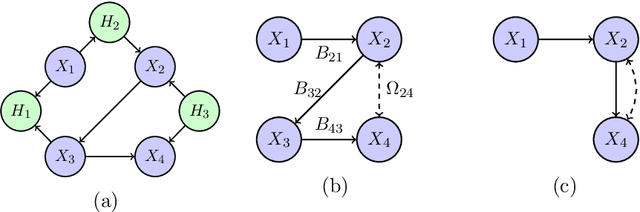
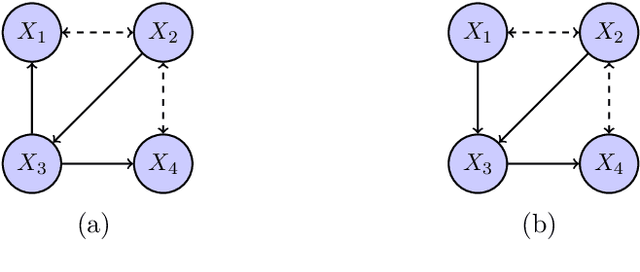
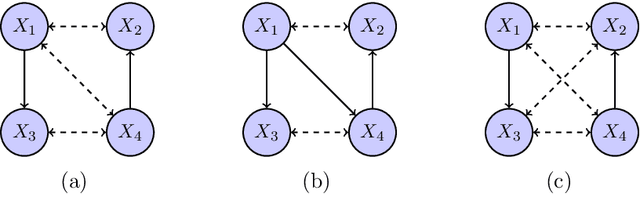
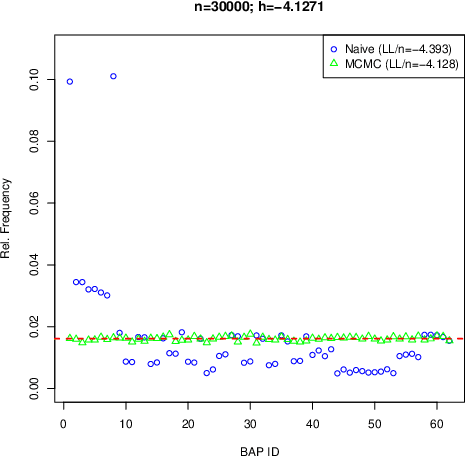
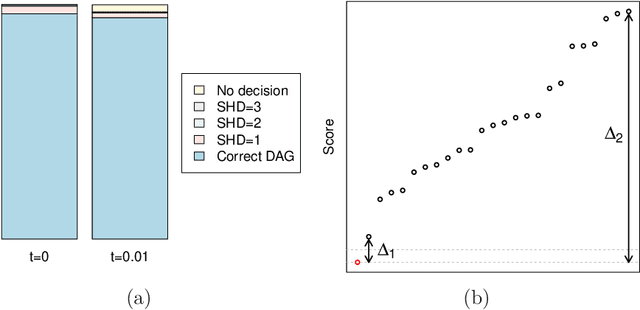
We consider the problem of structure learning for bow-free acyclic path diagrams (BAPs). BAPs can be viewed as a generalization of linear Gaussian DAG models that allow for certain hidden variables. We present a first method for this problem using a greedy score-based search algorithm. We also prove some necessary and some sufficient conditions for distributional equivalence of BAPs which are used in an algorithmic ap- proach to compute (nearly) equivalent model structures. This allows us to infer lower bounds of causal effects. We also present applications to real and simulated datasets using our publicly available R-package.

Score-based Causal Learning in Additive Noise Models

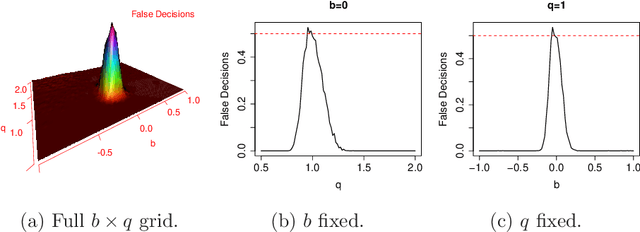
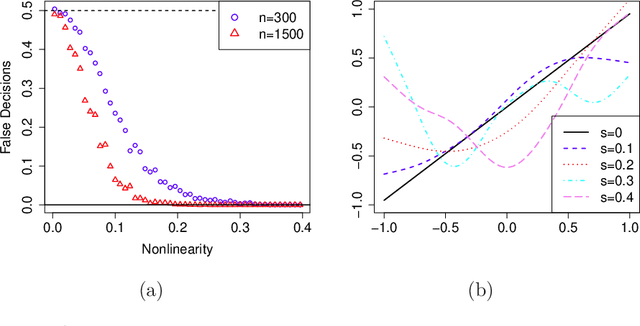
Given data sampled from a number of variables, one is often interested in the underlying causal relationships in the form of a directed acyclic graph. In the general case, without interventions on some of the variables it is only possible to identify the graph up to its Markov equivalence class. However, in some situations one can find the true causal graph just from observational data, for example in structural equation models with additive noise and nonlinear edge functions. Most current methods for achieving this rely on nonparametric independence tests. One of the problems there is that the null hypothesis is independence, which is what one would like to get evidence for. We take a different approach in our work by using a penalized likelihood as a score for model selection. This is practically feasible in many settings and has the advantage of yielding a natural ranking of the candidate models. When making smoothness assumptions on the probability density space, we prove consistency of the penalized maximum likelihood estimator. We also present empirical results for simulated scenarios and real two-dimensional data sets (cause-effect pairs) where we obtain similar results as other state-of-the-art methods.