Doubly Robust Kernel Statistics for Testing Distributional Treatment Effects Even Under One Sided Overlap

As causal inference becomes more widespread the importance of having good tools to test for causal effects increases. In this work we focus on the problem of testing for causal effects that manifest in a difference in distribution for treatment and control. We build on work applying kernel methods to causality, considering the previously introduced Counterfactual Mean Embedding framework (\textsc{CfME}). We improve on this by proposing the \emph{Doubly Robust Counterfactual Mean Embedding} (\textsc{DR-CfME}), which has better theoretical properties than its predecessor by leveraging semiparametric theory. This leads us to propose new kernel based test statistics for distributional effects which are based upon doubly robust estimators of treatment effects. We propose two test statistics, one which is a direct improvement on previous work and one which can be applied even when the support of the treatment arm is a subset of that of the control arm. We demonstrate the validity of our methods on simulated and real-world data, as well as giving an application in off-policy evaluation.

Explaining Preferences with Shapley Values

While preference modelling is becoming one of the pillars of machine learning, the problem of preference explanation remains challenging and underexplored. In this paper, we propose \textsc{Pref-SHAP}, a Shapley value-based model explanation framework for pairwise comparison data. We derive the appropriate value functions for preference models and further extend the framework to model and explain \emph{context specific} information, such as the surface type in a tennis game. To demonstrate the utility of \textsc{Pref-SHAP}, we apply our method to a variety of synthetic and real-world datasets and show that richer and more insightful explanations can be obtained over the baseline.

Generalized Variational Inference in Function Spaces: Gaussian Measures meet Bayesian Deep Learning

We develop a framework for generalized variational inference in infinite-dimensional function spaces and use it to construct a method termed Gaussian Wasserstein inference (GWI). GWI leverages the Wasserstein distance between Gaussian measures on the Hilbert space of square-integrable functions in order to determine a variational posterior using a tractable optimisation criterion and avoids pathologies arising in standard variational function space inference. An exciting application of GWI is the ability to use deep neural networks in the variational parametrisation of GWI, combining their superior predictive performance with the principled uncertainty quantification analogous to that of Gaussian processes. The proposed method obtains state-of-the-art performance on several benchmark datasets.

Giga-scale Kernel Matrix Vector Multiplication on GPU

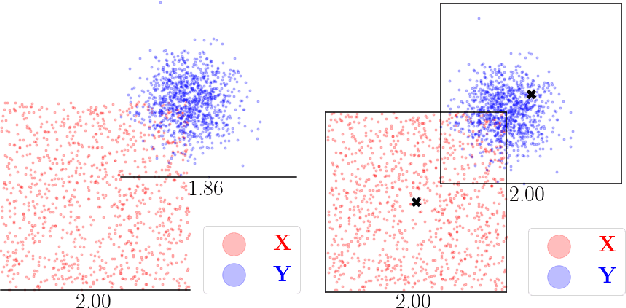
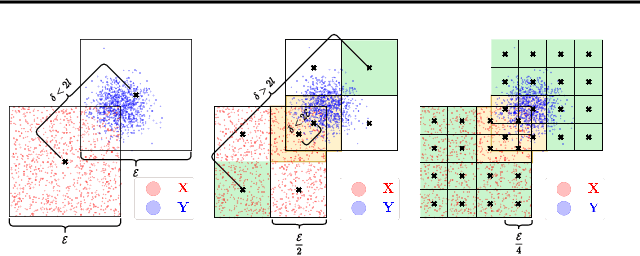
Kernel matrix vector multiplication (KMVM) is a ubiquitous operation in machine learning and scientific computing, spanning from the kernel literature to signal processing. As kernel matrix vector multiplication tends to scale quadratically in both memory and time, applications are often limited by these computational scaling constraints. We propose a novel approximation procedure coined Faster-Fast and Free Memory Method ($\text{F}^3$M) to address these scaling issues for KMVM. Extensive experiments demonstrate that $\text{F}^3$M has empirical \emph{linear time and memory} complexity with a relative error of order $10^{-3}$ and can compute a full KMVM for a billion points \emph{in under one minute} on a high-end GPU, leading to a significant speed-up in comparison to existing CPU methods. We further demonstrate the utility of our procedure by applying it as a drop-in for the state-of-the-art GPU-based linear solver FALKON, \emph{improving speed 3-5 times} at the cost of $<$1\% drop in accuracy.

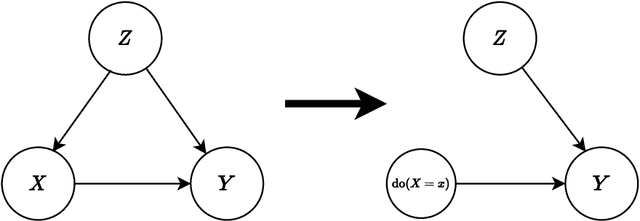
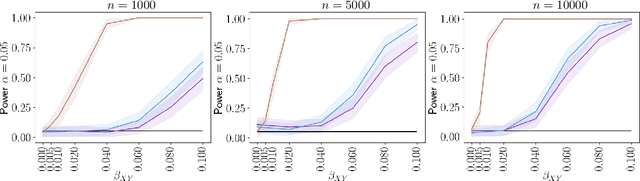
A Kernel Test for Causal Association via Noise Contrastive Backdoor Adjustment

Causal inference grows increasingly complex as the number of confounders increases. Given treatments $X$, confounders $Z$ and outcomes $Y$, we develop a non-parametric method to test the \textit{do-null} hypothesis $H_0:\; p(y|\text{\it do}(X=x))=p(y)$ against the general alternative. Building on the Hilbert Schmidt Independence Criterion (HSIC) for marginal independence testing, we propose backdoor-HSIC (bd-HSIC) and demonstrate that it is calibrated and has power for both binary and continuous treatments under a large number of confounders. Additionally, we establish convergence properties of the estimators of covariance operators used in bd-HSIC. We investigate the advantages and disadvantages of bd-HSIC against parametric tests as well as the importance of using the do-null testing in contrast to marginal independence testing or conditional independence testing. A complete implementation can be found at \hyperlink{https://github.com/MrHuff/kgformula}{\texttt{https://github.com/MrHuff/kgformula}}.

Time-to-event regression using partially monotonic neural networks

We propose a novel method, termed SuMo-net, that uses partially monotonic neural networks to learn a time-to-event distribution from a sample of covariates and right-censored times. SuMo-net models the survival function and the density jointly, and optimizes the likelihood for right-censored data instead of the often used partial likelihood. The method does not make assumptions about the true survival distribution and avoids computationally expensive integration of the hazard function. We evaluate the performance of the method on a range of datasets and find competitive performance across different metrics and improved computational time of making new predictions.

Large Scale Tensor Regression using Kernels and Variational Inference

We outline an inherent weakness of tensor factorization models when latent factors are expressed as a function of side information and propose a novel method to mitigate this weakness. We coin our method \textit{Kernel Fried Tensor}(KFT) and present it as a large scale forecasting tool for high dimensional data. Our results show superior performance against \textit{LightGBM} and \textit{Field Aware Factorization Machines}(FFM), two algorithms with proven track records widely used in industrial forecasting. We also develop a variational inference framework for KFT and associate our forecasts with calibrated uncertainty estimates on three large scale datasets. Furthermore, KFT is empirically shown to be robust against uninformative side information in terms of constants and Gaussian noise.