An Embedded Diachronic Sense Change Model with a Case Study from Ancient Greek

Word meanings change over time, and word senses evolve, emerge or die out in the process. For ancient languages, where the corpora are often small, sparse and noisy, modelling such changes accurately proves challenging, and quantifying uncertainty in sense-change estimates consequently becomes important. GASC and DiSC are existing generative models that have been used to analyse sense change for target words from an ancient Greek text corpus, using unsupervised learning without the help of any pre-training. These models represent the senses of a given target word such as "kosmos" (meaning decoration, order or world) as distributions over context words, and sense prevalence as a distribution over senses. The models are fitted using MCMC methods to measure temporal changes in these representations. In this paper, we introduce EDiSC, an embedded version of DiSC, which combines word embeddings with DiSC to provide superior model performance. We show empirically that EDiSC offers improved predictive accuracy, ground-truth recovery and uncertainty quantification, as well as better sampling efficiency and scalability properties with MCMC methods. We also discuss the challenges of fitting these models.

Scalable Semi-Modular Inference with Variational Meta-Posteriors

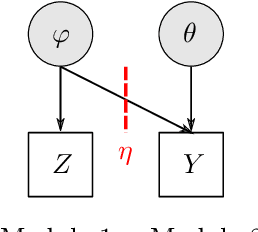
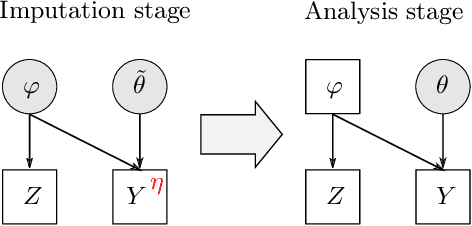
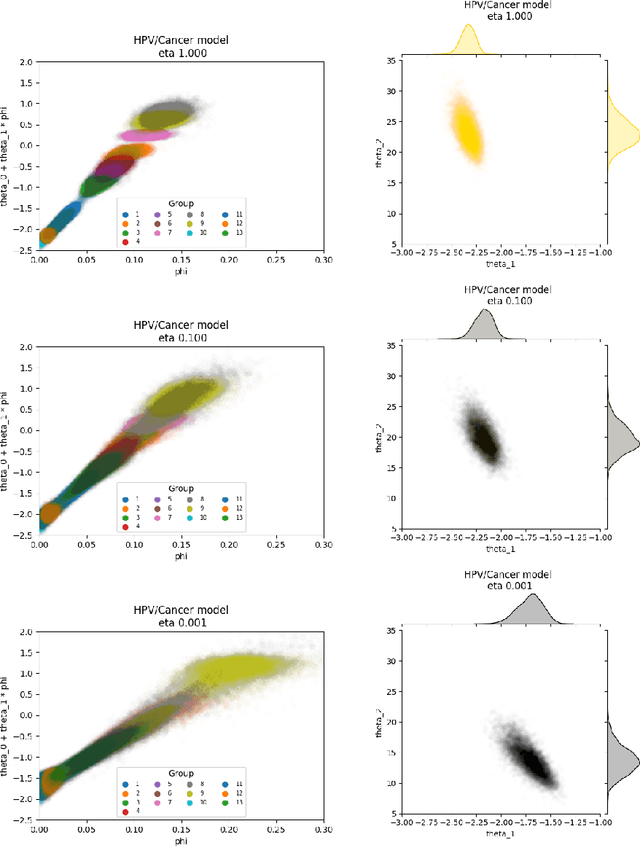
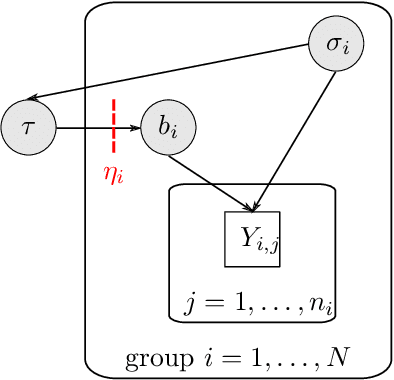
The Cut posterior and related Semi-Modular Inference are Generalised Bayes methods for Modular Bayesian evidence combination. Analysis is broken up over modular sub-models of the joint posterior distribution. Model-misspecification in multi-modular models can be hard to fix by model elaboration alone and the Cut posterior and SMI offer a way round this. Information entering the analysis from misspecified modules is controlled by an influence parameter $\eta$ related to the learning rate. This paper contains two substantial new methods. First, we give variational methods for approximating the Cut and SMI posteriors which are adapted to the inferential goals of evidence combination. We parameterise a family of variational posteriors using a Normalising Flow for accurate approximation and end-to-end training. Secondly, we show that analysis of models with multiple cuts is feasible using a new Variational Meta-Posterior. This approximates a family of SMI posteriors indexed by $\eta$ using a single set of variational parameters.

Semi-Modular Inference: enhanced learning in multi-modular models by tempering the influence of components

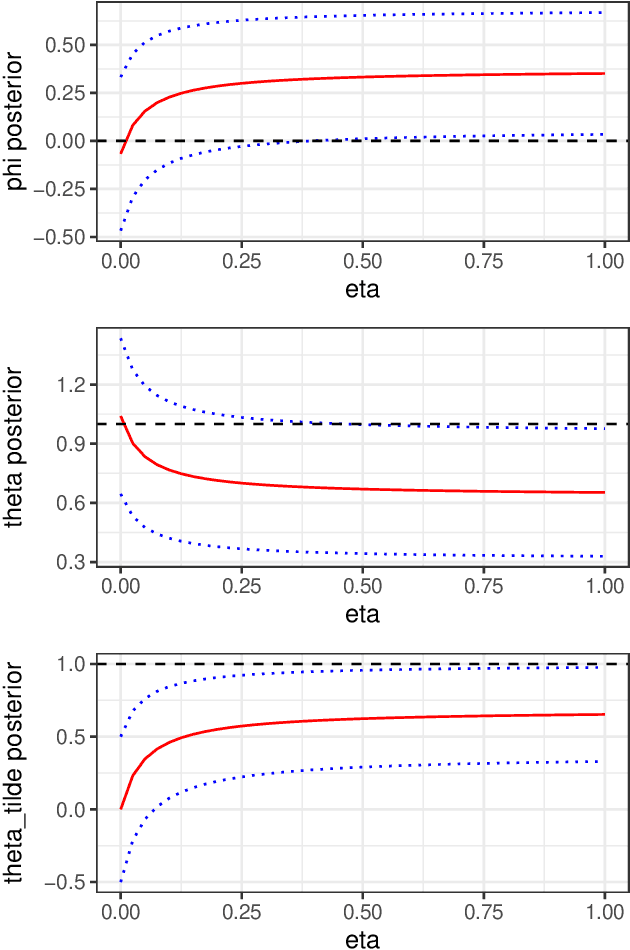
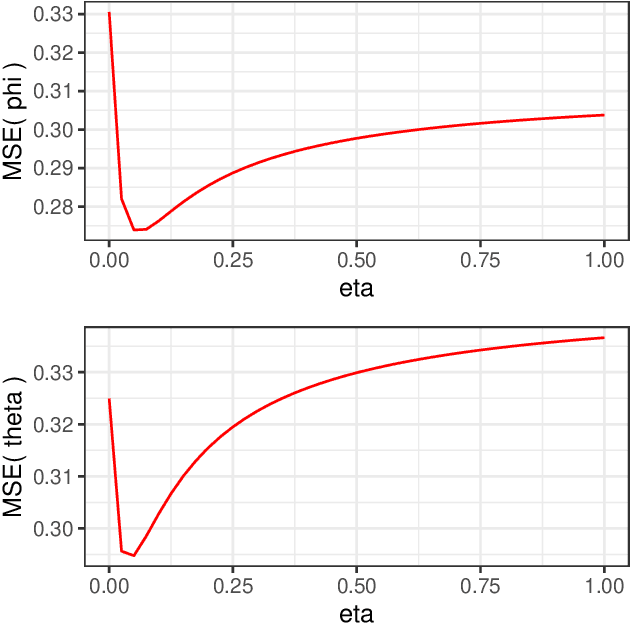
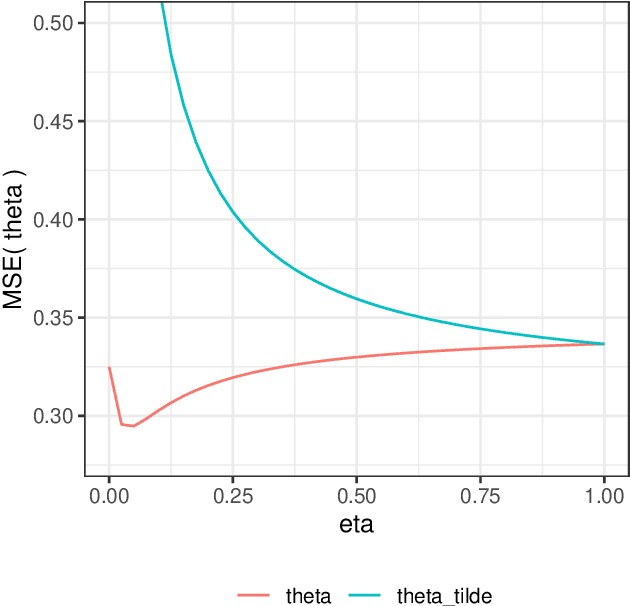
Bayesian statistical inference loses predictive optimality when generative models are misspecified. Working within an existing coherent loss-based generalisation of Bayesian inference, we show existing Modular/Cut-model inference is coherent, and write down a new family of Semi-Modular Inference (SMI) schemes, indexed by an influence parameter, with Bayesian inference and Cut-models as special cases. We give a meta-learning criterion and estimation procedure to choose the inference scheme. This returns Bayesian inference when there is no misspecification. The framework applies naturally to Multi-modular models. Cut-model inference allows directed information flow from well-specified modules to misspecified modules, but not vice versa. An existing alternative power posterior method gives tunable but undirected control of information flow, improving prediction in some settings. In contrast, SMI allows tunable and directed information flow between modules. We illustrate our methods on two standard test cases from the literature and a motivating archaeological data set.

Large Scale Tensor Regression using Kernels and Variational Inference

We outline an inherent weakness of tensor factorization models when latent factors are expressed as a function of side information and propose a novel method to mitigate this weakness. We coin our method \textit{Kernel Fried Tensor}(KFT) and present it as a large scale forecasting tool for high dimensional data. Our results show superior performance against \textit{LightGBM} and \textit{Field Aware Factorization Machines}(FFM), two algorithms with proven track records widely used in industrial forecasting. We also develop a variational inference framework for KFT and associate our forecasts with calibrated uncertainty estimates on three large scale datasets. Furthermore, KFT is empirically shown to be robust against uninformative side information in terms of constants and Gaussian noise.