Scalable Semi-Modular Inference with Variational Meta-Posteriors
Paper and Code
Apr 01, 2022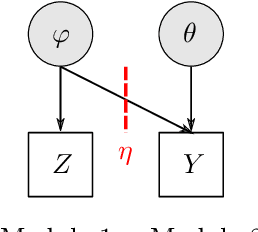
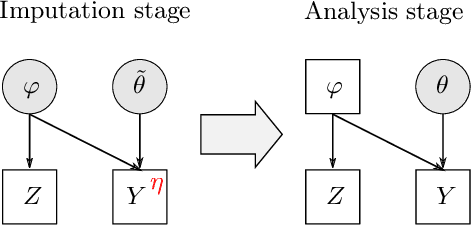
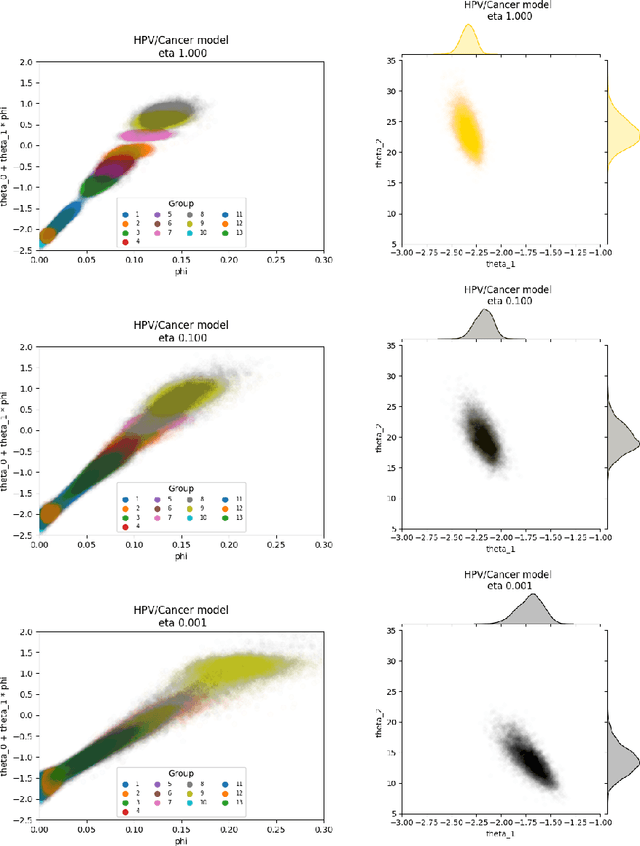
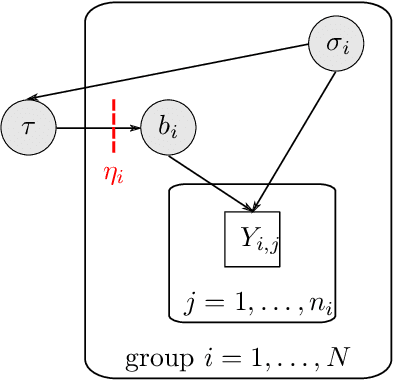
The Cut posterior and related Semi-Modular Inference are Generalised Bayes methods for Modular Bayesian evidence combination. Analysis is broken up over modular sub-models of the joint posterior distribution. Model-misspecification in multi-modular models can be hard to fix by model elaboration alone and the Cut posterior and SMI offer a way round this. Information entering the analysis from misspecified modules is controlled by an influence parameter $\eta$ related to the learning rate. This paper contains two substantial new methods. First, we give variational methods for approximating the Cut and SMI posteriors which are adapted to the inferential goals of evidence combination. We parameterise a family of variational posteriors using a Normalising Flow for accurate approximation and end-to-end training. Secondly, we show that analysis of models with multiple cuts is feasible using a new Variational Meta-Posterior. This approximates a family of SMI posteriors indexed by $\eta$ using a single set of variational parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge