Scalable Semi-Modular Inference with Variational Meta-Posteriors

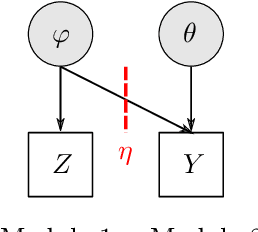
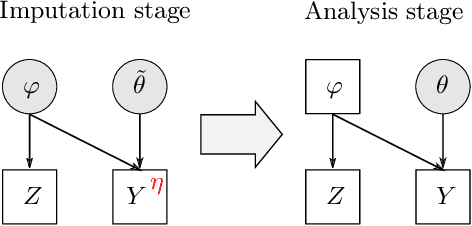
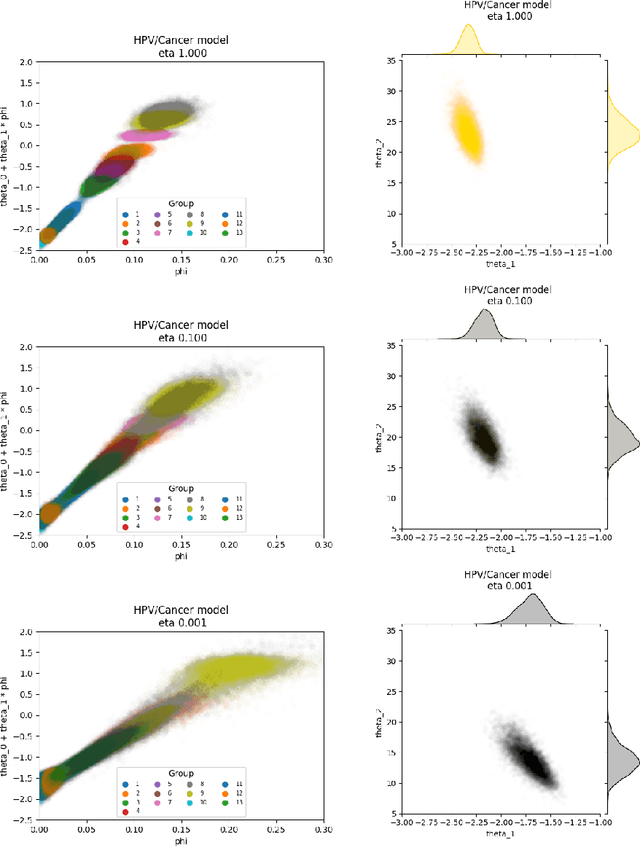
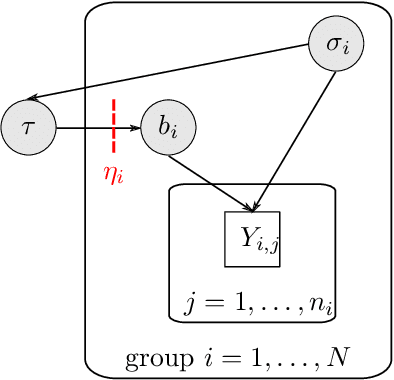
The Cut posterior and related Semi-Modular Inference are Generalised Bayes methods for Modular Bayesian evidence combination. Analysis is broken up over modular sub-models of the joint posterior distribution. Model-misspecification in multi-modular models can be hard to fix by model elaboration alone and the Cut posterior and SMI offer a way round this. Information entering the analysis from misspecified modules is controlled by an influence parameter $\eta$ related to the learning rate. This paper contains two substantial new methods. First, we give variational methods for approximating the Cut and SMI posteriors which are adapted to the inferential goals of evidence combination. We parameterise a family of variational posteriors using a Normalising Flow for accurate approximation and end-to-end training. Secondly, we show that analysis of models with multiple cuts is feasible using a new Variational Meta-Posterior. This approximates a family of SMI posteriors indexed by $\eta$ using a single set of variational parameters.

Neural Contextual Anomaly Detection for Time Series

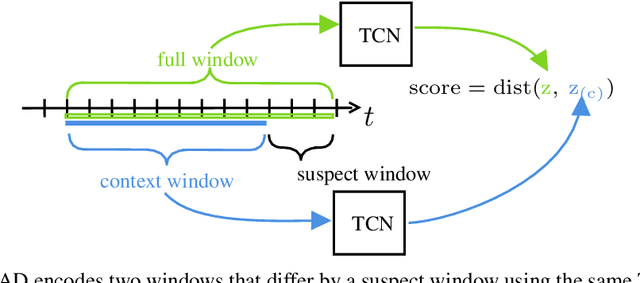
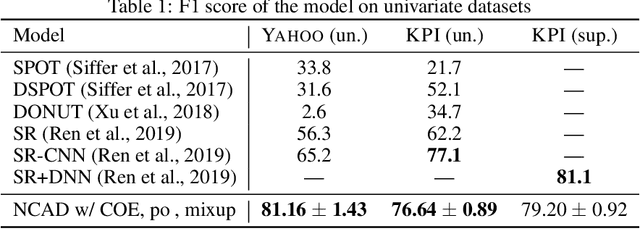
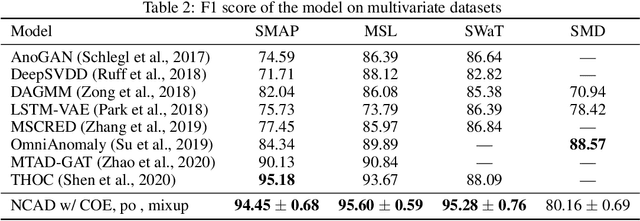
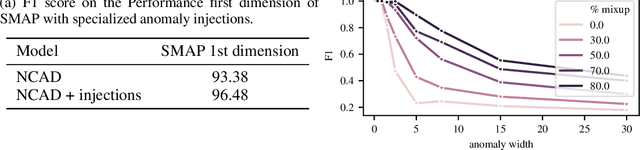
We introduce Neural Contextual Anomaly Detection (NCAD), a framework for anomaly detection on time series that scales seamlessly from the unsupervised to supervised setting, and is applicable to both univariate and multivariate time series. This is achieved by effectively combining recent developments in representation learning for multivariate time series, with techniques for deep anomaly detection originally developed for computer vision that we tailor to the time series setting. Our window-based approach facilitates learning the boundary between normal and anomalous classes by injecting generic synthetic anomalies into the available data. Moreover, our method can effectively take advantage of all the available information, be it as domain knowledge, or as training labels in the semi-supervised setting. We demonstrate empirically on standard benchmark datasets that our approach obtains a state-of-the-art performance in these settings.

Semi-Modular Inference: enhanced learning in multi-modular models by tempering the influence of components

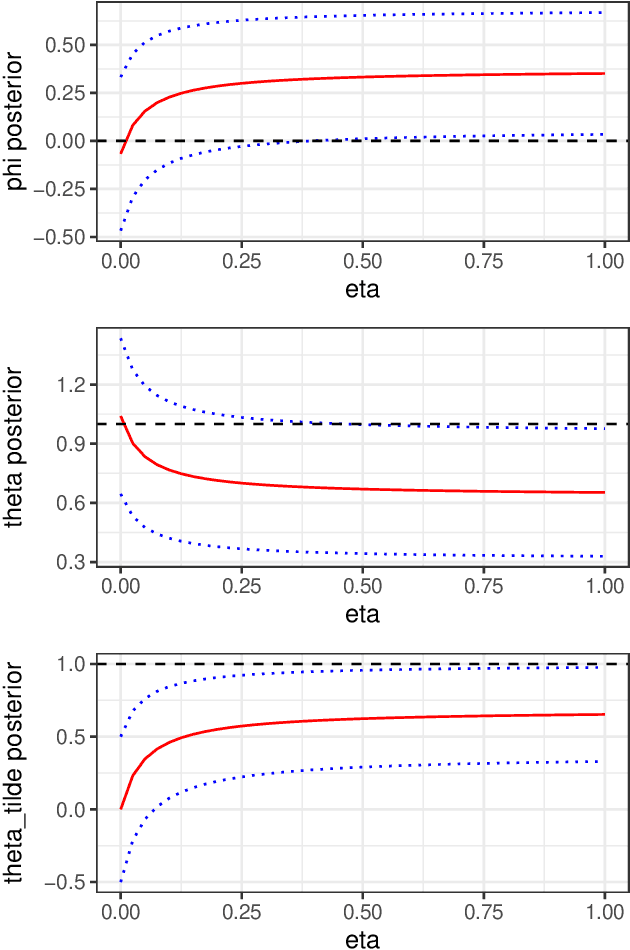
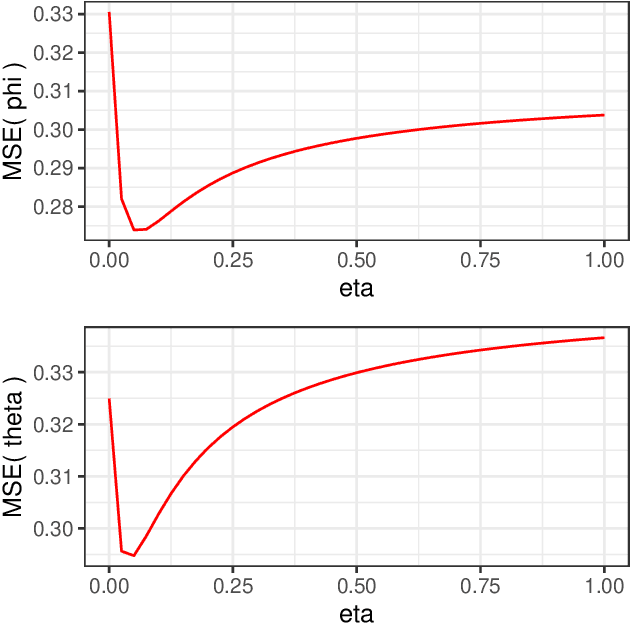
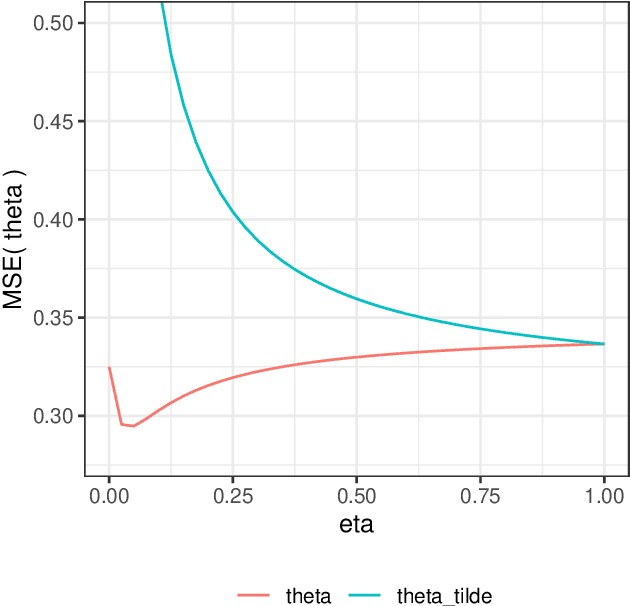
Bayesian statistical inference loses predictive optimality when generative models are misspecified. Working within an existing coherent loss-based generalisation of Bayesian inference, we show existing Modular/Cut-model inference is coherent, and write down a new family of Semi-Modular Inference (SMI) schemes, indexed by an influence parameter, with Bayesian inference and Cut-models as special cases. We give a meta-learning criterion and estimation procedure to choose the inference scheme. This returns Bayesian inference when there is no misspecification. The framework applies naturally to Multi-modular models. Cut-model inference allows directed information flow from well-specified modules to misspecified modules, but not vice versa. An existing alternative power posterior method gives tunable but undirected control of information flow, improving prediction in some settings. In contrast, SMI allows tunable and directed information flow between modules. We illustrate our methods on two standard test cases from the literature and a motivating archaeological data set.