Giga-scale Kernel Matrix Vector Multiplication on GPU
Paper and Code
Feb 02, 2022
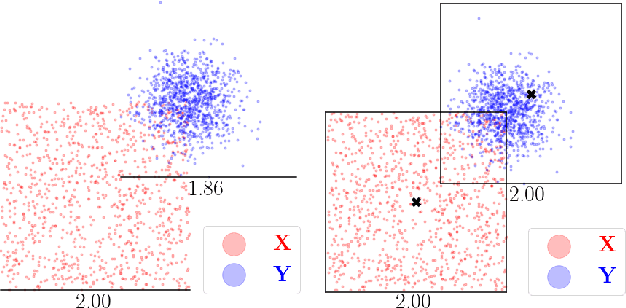
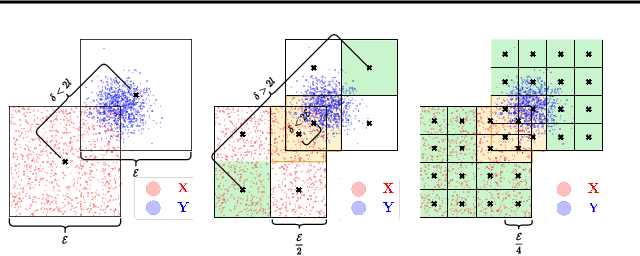

Kernel matrix vector multiplication (KMVM) is a ubiquitous operation in machine learning and scientific computing, spanning from the kernel literature to signal processing. As kernel matrix vector multiplication tends to scale quadratically in both memory and time, applications are often limited by these computational scaling constraints. We propose a novel approximation procedure coined Faster-Fast and Free Memory Method ($\text{F}^3$M) to address these scaling issues for KMVM. Extensive experiments demonstrate that $\text{F}^3$M has empirical \emph{linear time and memory} complexity with a relative error of order $10^{-3}$ and can compute a full KMVM for a billion points \emph{in under one minute} on a high-end GPU, leading to a significant speed-up in comparison to existing CPU methods. We further demonstrate the utility of our procedure by applying it as a drop-in for the state-of-the-art GPU-based linear solver FALKON, \emph{improving speed 3-5 times} at the cost of $<$1\% drop in accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge