Influence Functions for Machine Learning: Nonparametric Estimators for Entropies, Divergences and Mutual Informations
Paper and Code
Jun 19, 2015
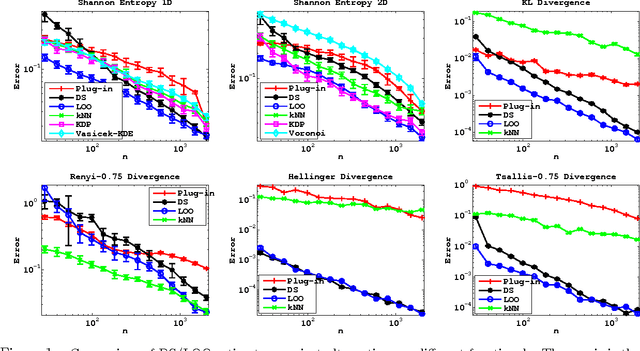
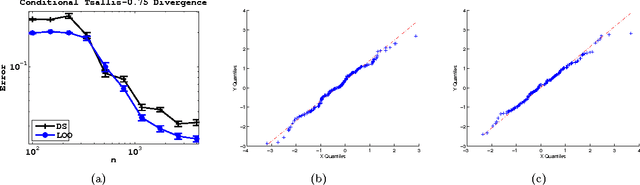

We propose and analyze estimators for statistical functionals of one or more distributions under nonparametric assumptions. Our estimators are based on the theory of influence functions, which appear in the semiparametric statistics literature. We show that estimators based either on data-splitting or a leave-one-out technique enjoy fast rates of convergence and other favorable theoretical properties. We apply this framework to derive estimators for several popular information theoretic quantities, and via empirical evaluation, show the advantage of this approach over existing estimators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge