Transfer Learning for Classification under Decision Rule Drift with Application to Optimal Individualized Treatment Rule Estimation

In this paper, we extend the transfer learning classification framework from regression function-based methods to decision rules. We propose a novel methodology for modeling posterior drift through Bayes decision rules. By exploiting the geometric transformation of the Bayes decision boundary, our method reformulates the problem as a low-dimensional empirical risk minimization problem. Under mild regularity conditions, we establish the consistency of our estimators and derive the risk bounds. Moreover, we illustrate the broad applicability of our method by adapting it to the estimation of optimal individualized treatment rules. Extensive simulation studies and analyses of real-world data further demonstrate both superior performance and robustness of our approach.

Token-Importance Guided Direct Preference Optimization

Ensuring that large language models (LLMs) generate outputs aligned with human preferences is important for safe and effective AI interactions. While Direct Preference Optimization (DPO) employs an implicit reward function to optimize the policy model, however, it and its related variants overlook the differential importance of individual tokens and are sensitive to judgment noise in preference datasets during generation. Although recent methods attempt to assess the important weight of tokens via probability prediction or simplistic weighting schemes, these evaluation methods are prone to biases and still cannot fully address these issues. To solve this problem, we propose the Token-Importance Guided Direct Preference Optimization (TI-DPO), which introduces two key innovations: the gradient-based token-importance weights that dynamically prioritize critical tokens, and a triple loss that explicitly guides model outputs to approach human-preferred responses and stay away from non-preferred responses. Experimental results show that TI-DPO achieves higher accuracy and stronger generative diversity, providing more stable and computationally efficient solutions compared with DPO and other RLHF methods.

Optimal Sampling for Generalized Linear Model under Measurement Constraint with Surrogate Variables

Measurement-constrained datasets, often encountered in semi-supervised learning, arise when data labeling is costly, time-intensive, or hindered by confidentiality or ethical concerns, resulting in a scarcity of labeled data. In certain cases, surrogate variables are accessible across the entire dataset and can serve as approximations to the true response variable; however, these surrogates often contain measurement errors and thus cannot be directly used for accurate prediction. We propose an optimal sampling strategy that effectively harnesses the available information from surrogate variables. This approach provides consistent estimators under the assumption of a generalized linear model, achieving theoretically lower asymptotic variance than existing optimal sampling algorithms that do not leverage surrogate data. By employing the A-optimality criterion from optimal experimental design, our strategy maximizes statistical efficiency. Numerical studies demonstrate that our approach surpasses existing optimal sampling methods, exhibiting reduced empirical mean squared error and enhanced robustness in algorithmic performance. These findings highlight the practical advantages of our strategy in scenarios where measurement constraints exist and surrogates are available.

Active Subsampling for Measurement-Constrained M-Estimation of Individualized Thresholds with High-Dimensional Data

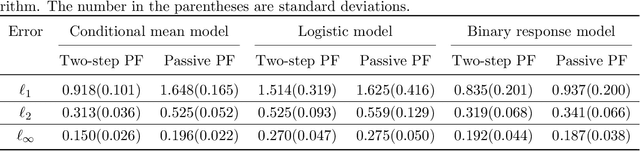
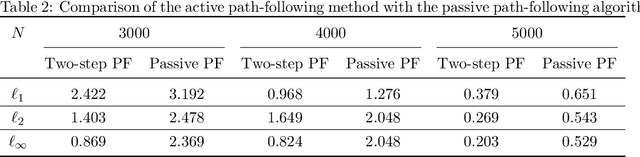
In the measurement-constrained problems, despite the availability of large datasets, we may be only affordable to observe the labels on a small portion of the large dataset. This poses a critical question that which data points are most beneficial to label given a budget constraint. In this paper, we focus on the estimation of the optimal individualized threshold in a measurement-constrained M-estimation framework. Our goal is to estimate a high-dimensional parameter $\theta$ in a linear threshold $\theta^T Z$ for a continuous variable $X$ such that the discrepancy between whether $X$ exceeds the threshold $\theta^T Z$ and a binary outcome $Y$ is minimized. We propose a novel $K$-step active subsampling algorithm to estimate $\theta$, which iteratively samples the most informative observations and solves a regularized M-estimator. The theoretical properties of our estimator demonstrate a phase transition phenomenon with respect to $\beta\geq 1$, the smoothness of the conditional density of $X$ given $Y$ and $Z$. For $\beta>(1+\sqrt{3})/2$, we show that the two-step algorithm yields an estimator with the parametric convergence rate $O_p((s \log d /N)^{1/2})$ in $l_2$ norm. The rate of our estimator is strictly faster than the minimax optimal rate with $N$ i.i.d. samples drawn from the population. For the other two scenarios $1<\beta\leq (1+\sqrt{3})/2$ and $\beta=1$, the estimator from the two-step algorithm is sub-optimal. The former requires to run $K>2$ steps to attain the same parametric rate, whereas in the latter case only a near parametric rate can be obtained. Furthermore, we formulate a minimax framework for the measurement-constrained M-estimation problem and prove that our estimator is minimax rate optimal up to a logarithmic factor. Finally, we demonstrate the performance of our method in simulation studies and apply the method to analyze a large diabetes dataset.

Inference with non-differentiable surrogate loss in a general high-dimensional classification framework

Penalized empirical risk minimization with a surrogate loss function is often used to derive a high-dimensional linear decision rule in classification problems. Although much of the literature focuses on the generalization error, there is a lack of valid inference procedures to identify the driving factors of the estimated decision rule, especially when the surrogate loss is non-differentiable. In this work, we propose a kernel-smoothed decorrelated score to construct hypothesis testing and interval estimations for the linear decision rule estimated using a piece-wise linear surrogate loss, which has a discontinuous gradient and non-regular Hessian. Specifically, we adopt kernel approximations to smooth the discontinuous gradient near discontinuity points and approximate the non-regular Hessian of the surrogate loss. In applications where additional nuisance parameters are involved, we propose a novel cross-fitted version to accommodate flexible nuisance estimates and kernel approximations. We establish the limiting distribution of the kernel-smoothed decorrelated score and its cross-fitted version in a high-dimensional setup. Simulation and real data analysis are conducted to demonstrate the validity and superiority of the proposed method.

Treatment Effect Estimation with Unobserved and Heterogeneous Confounding Variables

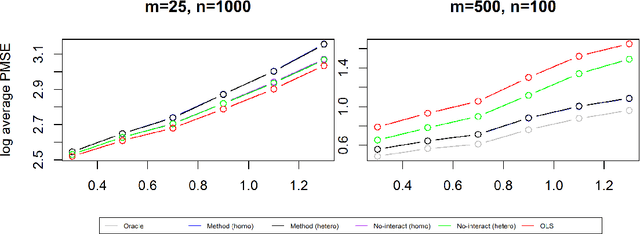
The estimation of the treatment effect is often biased in the presence of unobserved confounding variables which are commonly referred to as hidden variables. Although a few methods have been recently proposed to handle the effect of hidden variables, these methods often overlook the possibility of any interaction between the observed treatment variable and the unobserved covariates. In this work, we address this shortcoming by studying a multivariate response regression problem with both unobserved and heterogeneous confounding variables of the form $Y=A^T X+ B^T Z+ \sum_{j=1}^{p} C^T_j X_j Z + E$, where $Y \in \mathbb{R}^m$ are $m$-dimensional response variables, $X \in \mathbb{R}^p$ are observed covariates (including the treatment variable), $Z \in \mathbb{R}^K$ are $K$-dimensional unobserved confounders, and $E \in \mathbb{R}^m$ is the random noise. Allowing for the interaction between $X_j$ and $Z$ induces the heterogeneous confounding effect. Our goal is to estimate the unknown matrix $A$, the direct effect of the observed covariates or the treatment on the responses. To this end, we propose a new debiased estimation approach via SVD to remove the effect of unobserved confounding variables. The rate of convergence of the estimator is established under both the homoscedastic and heteroscedastic noises. We also present several simulation experiments and a real-world data application to substantiate our findings.

Optimal Variable Clustering for High-Dimensional Matrix Valued Data

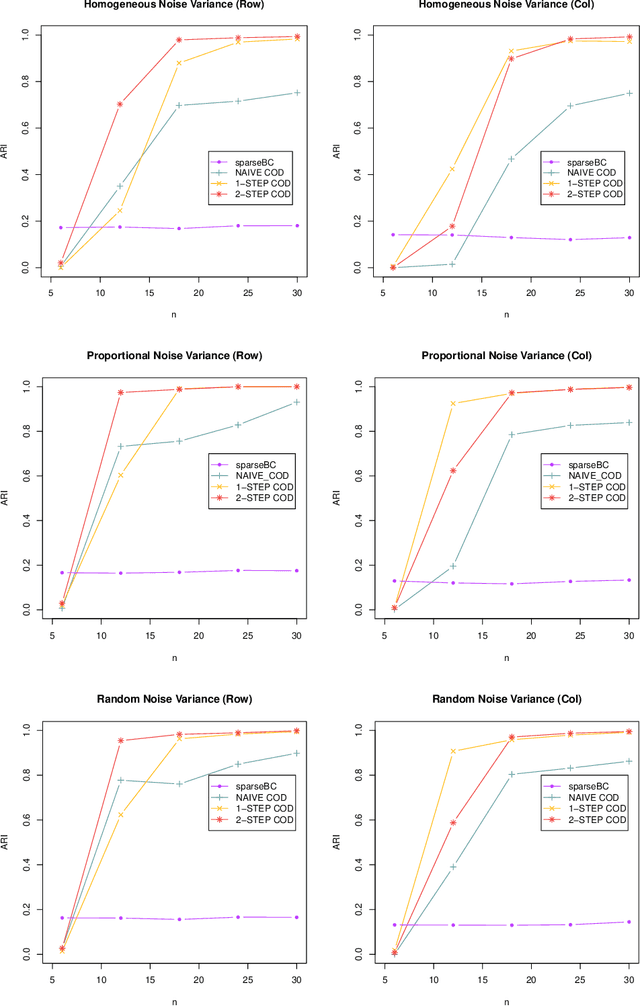
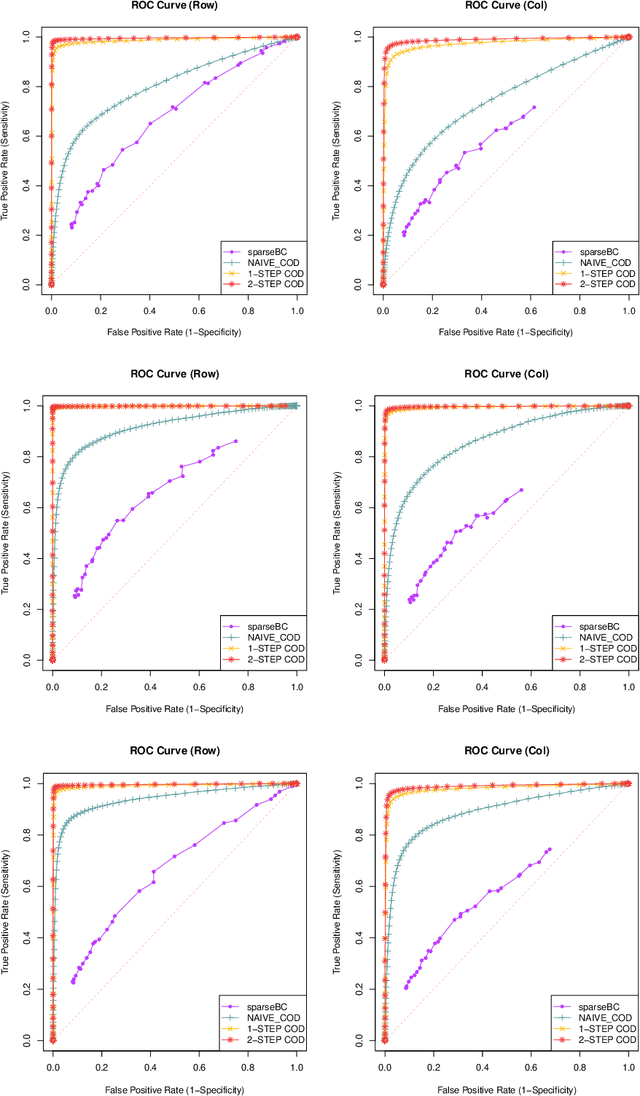
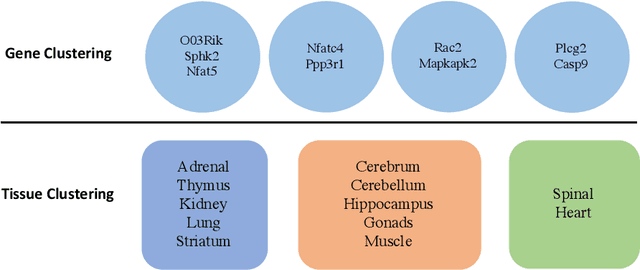
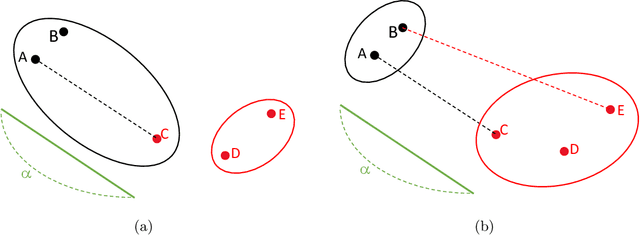
Matrix valued data has become increasingly prevalent in many applications. Most of the existing clustering methods for this type of data are tailored to the mean model and do not account for the dependence structure of the features, which can be very informative, especially in high-dimensional settings. To extract the information from the dependence structure for clustering, we propose a new latent variable model for the features arranged in matrix form, with some unknown membership matrices representing the clusters for the rows and columns. Under this model, we further propose a class of hierarchical clustering algorithms using the difference of a weighted covariance matrix as the dissimilarity measure. Theoretically, we show that under mild conditions, our algorithm attains clustering consistency in the high-dimensional setting. While this consistency result holds for our algorithm with a broad class of weighted covariance matrices, the conditions for this result depend on the choice of the weight. To investigate how the weight affects the theoretical performance of our algorithm, we establish the minimax lower bound for clustering under our latent variable model. Given these results, we identify the optimal weight in the sense that using this weight guarantees our algorithm to be minimax rate-optimal in terms of the magnitude of some cluster separation metric. The practical implementation of our algorithm with the optimal weight is also discussed. Finally, we conduct simulation studies to evaluate the finite sample performance of our algorithm and apply the method to a genomic dataset.

Optimal Semi-supervised Estimation and Inference for High-dimensional Linear Regression

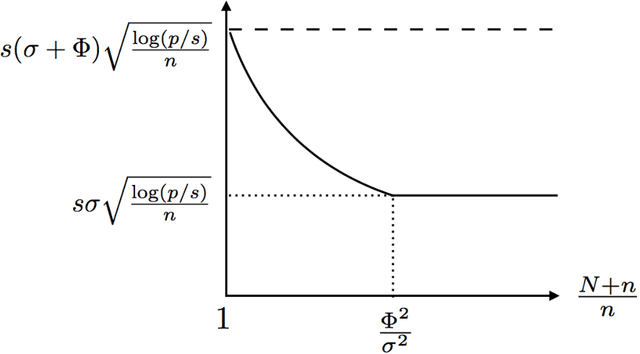
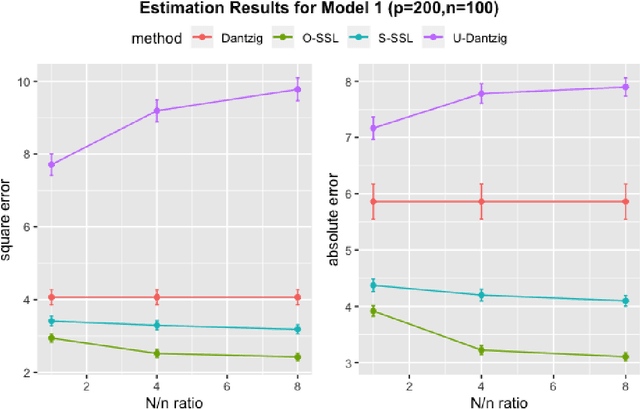
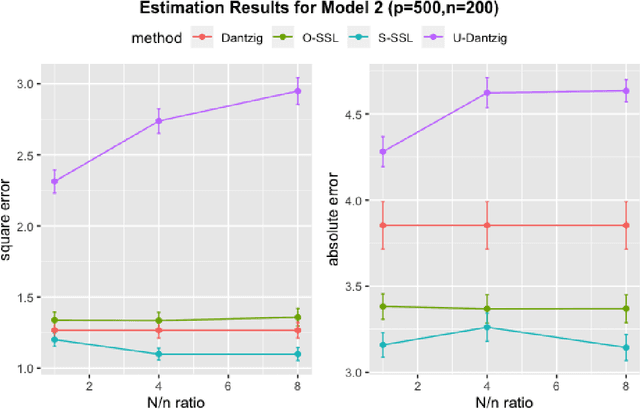
There are many scenarios such as the electronic health records where the outcome is much more difficult to collect than the covariates. In this paper, we consider the linear regression problem with such a data structure under the high dimensionality. Our goal is to investigate when and how the unlabeled data can be exploited to improve the estimation and inference of the regression parameters in linear models, especially in light of the fact that such linear models may be misspecified in data analysis. In particular, we address the following two important questions. (1) Can we use the labeled data as well as the unlabeled data to construct a semi-supervised estimator such that its convergence rate is faster than the supervised estimators? (2) Can we construct confidence intervals or hypothesis tests that are guaranteed to be more efficient or powerful than the supervised estimators? To address the first question, we establish the minimax lower bound for parameter estimation in the semi-supervised setting. We show that the upper bound from the supervised estimators that only use the labeled data cannot attain this lower bound. We close this gap by proposing a new semi-supervised estimator which attains the lower bound. To address the second question, based on our proposed semi-supervised estimator, we propose two additional estimators for semi-supervised inference, the efficient estimator and the safe estimator. The former is fully efficient if the unknown conditional mean function is estimated consistently, but may not be more efficient than the supervised approach otherwise. The latter usually does not aim to provide fully efficient inference, but is guaranteed to be no worse than the supervised approach, no matter whether the linear model is correctly specified or the conditional mean function is consistently estimated.

Doubly Robust Semiparametric Difference-in-Differences Estimators with High-Dimensional Data

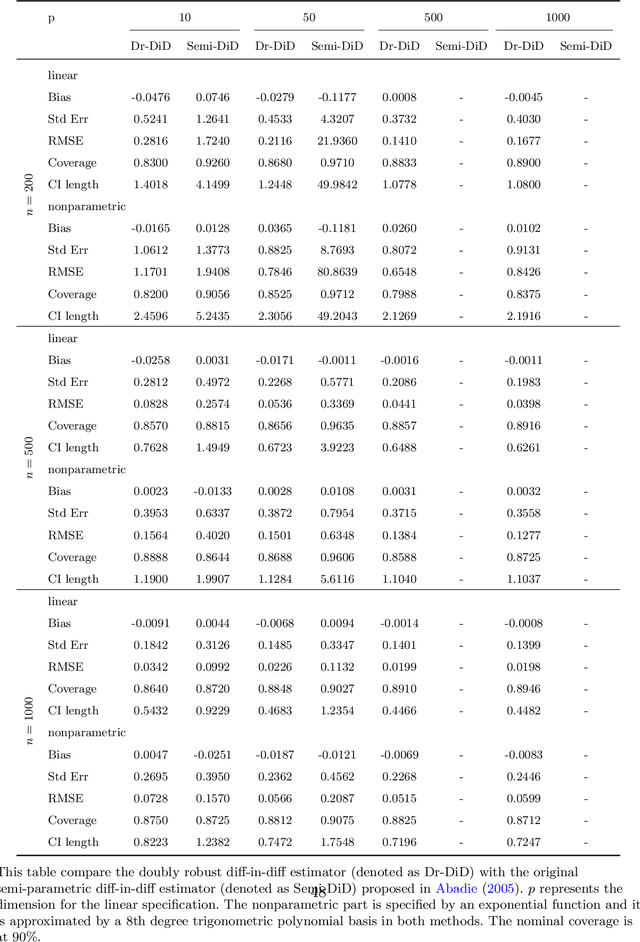
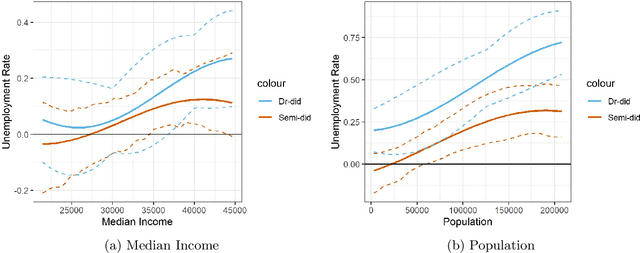
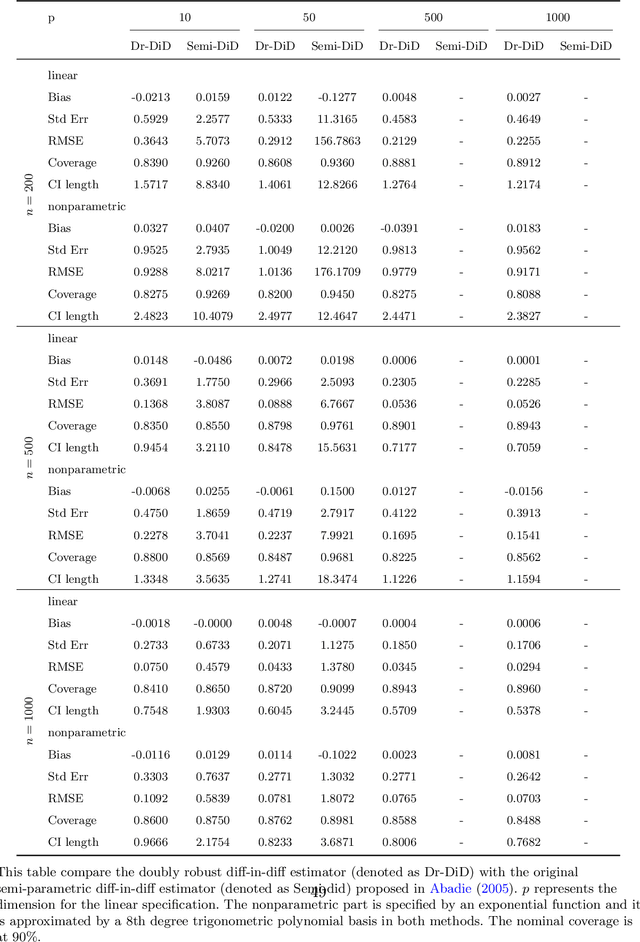
This paper proposes a doubly robust two-stage semiparametric difference-in-difference estimator for estimating heterogeneous treatment effects with high-dimensional data. Our new estimator is robust to model miss-specifications and allows for, but does not require, many more regressors than observations. The first stage allows a general set of machine learning methods to be used to estimate the propensity score. In the second stage, we derive the rates of convergence for both the parametric parameter and the unknown function under a partially linear specification for the outcome equation. We also provide bias correction procedures to allow for valid inference for the heterogeneous treatment effects. We evaluate the finite sample performance with extensive simulation studies. Additionally, a real data analysis on the effect of Fair Minimum Wage Act on the unemployment rate is performed as an illustration of our method. An R package for implementing the proposed method is available on Github.

Regularized Training and Tight Certification for Randomized Smoothed Classifier with Provable Robustness

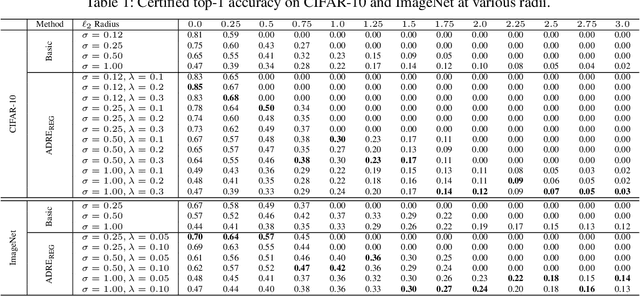
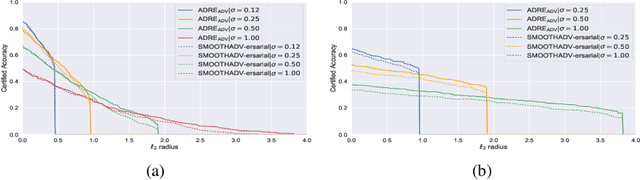
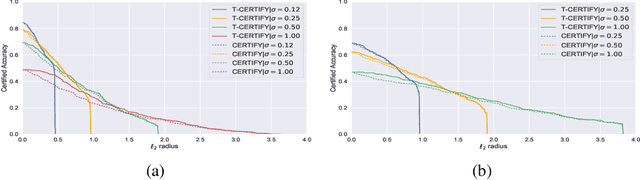
Recently smoothing deep neural network based classifiers via isotropic Gaussian perturbation is shown to be an effective and scalable way to provide state-of-the-art probabilistic robustness guarantee against $\ell_2$ norm bounded adversarial perturbations. However, how to train a good base classifier that is accurate and robust when smoothed has not been fully investigated. In this work, we derive a new regularized risk, in which the regularizer can adaptively encourage the accuracy and robustness of the smoothed counterpart when training the base classifier. It is computationally efficient and can be implemented in parallel with other empirical defense methods. We discuss how to implement it under both standard (non-adversarial) and adversarial training scheme. At the same time, we also design a new certification algorithm, which can leverage the regularization effect to provide tighter robustness lower bound that holds with high probability. Our extensive experimentation demonstrates the effectiveness of the proposed training and certification approaches on CIFAR-10 and ImageNet datasets.