Inference with non-differentiable surrogate loss in a general high-dimensional classification framework

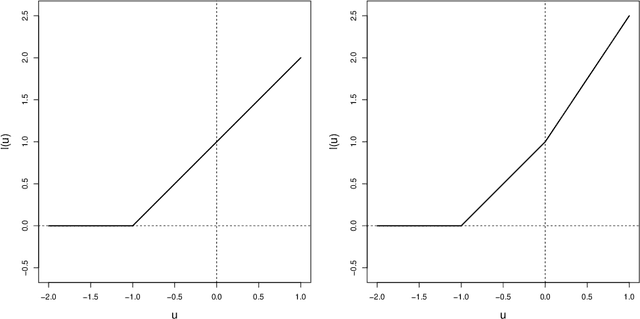
Penalized empirical risk minimization with a surrogate loss function is often used to derive a high-dimensional linear decision rule in classification problems. Although much of the literature focuses on the generalization error, there is a lack of valid inference procedures to identify the driving factors of the estimated decision rule, especially when the surrogate loss is non-differentiable. In this work, we propose a kernel-smoothed decorrelated score to construct hypothesis testing and interval estimations for the linear decision rule estimated using a piece-wise linear surrogate loss, which has a discontinuous gradient and non-regular Hessian. Specifically, we adopt kernel approximations to smooth the discontinuous gradient near discontinuity points and approximate the non-regular Hessian of the surrogate loss. In applications where additional nuisance parameters are involved, we propose a novel cross-fitted version to accommodate flexible nuisance estimates and kernel approximations. We establish the limiting distribution of the kernel-smoothed decorrelated score and its cross-fitted version in a high-dimensional setup. Simulation and real data analysis are conducted to demonstrate the validity and superiority of the proposed method.

Near-optimal Individualized Treatment Recommendations

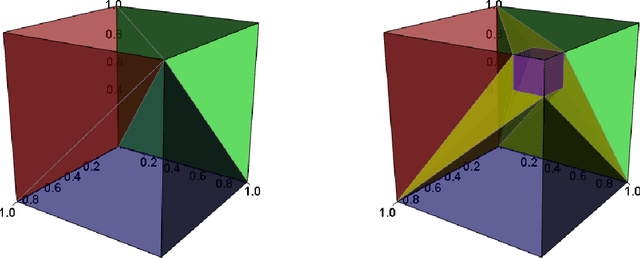
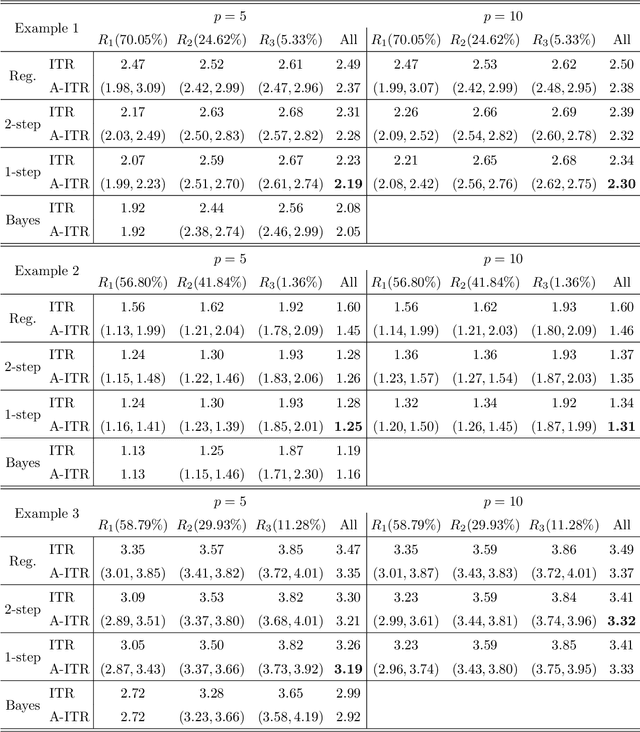
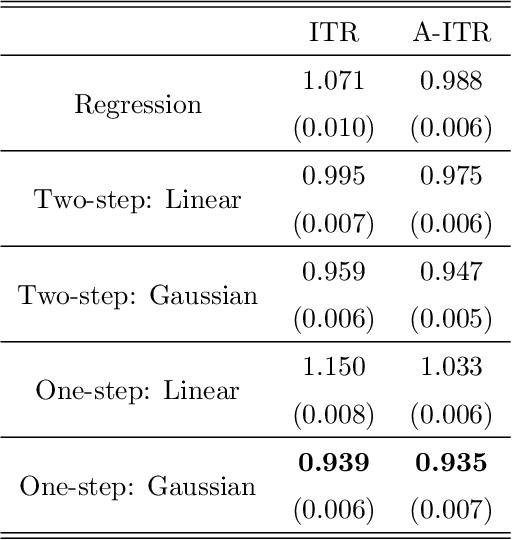
Individualized treatment recommendation (ITR) is an important analytic framework for precision medicine. The goal is to assign proper treatments to patients based on their individual characteristics. From the machine learning perspective, the solution to an ITR problem can be formulated as a weighted classification problem to maximize the average benefit that patients receive from the recommended treatments. Several methods have been proposed for ITR in both binary and multicategory treatment setups. In practice, one may prefer a more flexible recommendation with multiple treatment options. This motivates us to develop methods to obtain a set of near-optimal individualized treatment recommendations alternative to each other, called alternative individualized treatment recommendations (A-ITR). We propose two methods to estimate the optimal A-ITR within the outcome weighted learning (OWL) framework. We show the consistency of these methods and obtain an upper bound for the risk between the theoretically optimal recommendation and the estimated one. We also conduct simulation studies, and apply our methods to a real data set for Type 2 diabetic patients with injectable antidiabetic treatments. These numerical studies have shown the usefulness of the proposed A-ITR framework. We develop a R package aitr which can be found at https://github.com/menghaomiao/aitr.