Fast Approximation of the Shapley Values Based on Order-of-Addition Experimental Designs

Shapley value is originally a concept in econometrics to fairly distribute both gains and costs to players in a coalition game. In the recent decades, its application has been extended to other areas such as marketing, engineering and machine learning. For example, it produces reasonable solutions for problems in sensitivity analysis, local model explanation towards the interpretable machine learning, node importance in social network, attribution models, etc. However, its heavy computational burden has been long recognized but rarely investigated. Specifically, in a $d$-player coalition game, calculating a Shapley value requires the evaluation of $d!$ or $2^d$ marginal contribution values, depending on whether we are taking the permutation or combination formulation of the Shapley value. Hence it becomes infeasible to calculate the Shapley value when $d$ is reasonably large. A common remedy is to take a random sample of the permutations to surrogate for the complete list of permutations. We find an advanced sampling scheme can be designed to yield much more accurate estimation of the Shapley value than the simple random sampling (SRS). Our sampling scheme is based on combinatorial structures in the field of design of experiments (DOE), particularly the order-of-addition experimental designs for the study of how the orderings of components would affect the output. We show that the obtained estimates are unbiased, and can sometimes deterministically recover the original Shapley value. Both theoretical and simulations results show that our DOE-based sampling scheme outperforms SRS in terms of estimation accuracy. Surprisingly, it is also slightly faster than SRS. Lastly, real data analysis is conducted for the C. elegans nervous system and the 9/11 terrorist network.

Query-augmented Active Metric Learning

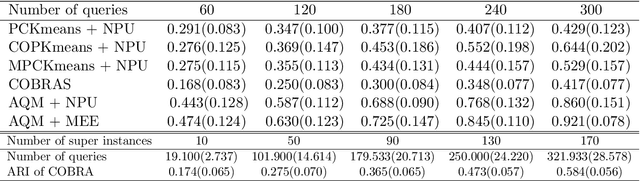
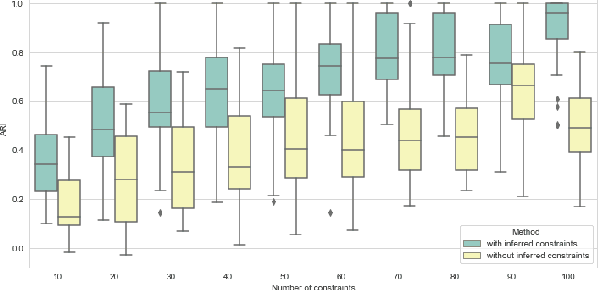
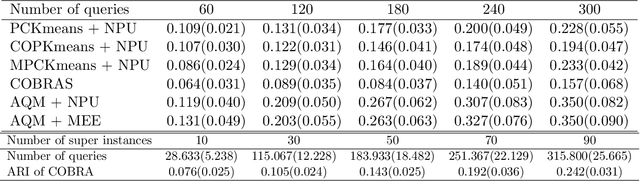
In this paper we propose an active metric learning method for clustering with pairwise constraints. The proposed method actively queries the label of informative instance pairs, while estimating underlying metrics by incorporating unlabeled instance pairs, which leads to a more accurate and efficient clustering process. In particular, we augment the queried constraints by generating more pairwise labels to provide additional information in learning a metric to enhance clustering performance. Furthermore, we increase the robustness of metric learning by updating the learned metric sequentially and penalizing the irrelevant features adaptively. In addition, we propose a novel active query strategy that evaluates the information gain of instance pairs more accurately by incorporating the neighborhood structure, which improves clustering efficiency without extra labeling cost. In theory, we provide a tighter error bound of the proposed metric learning method utilizing augmented queries compared with methods using existing constraints only. Furthermore, we also investigate the improvement using the active query strategy instead of random selection. Numerical studies on simulation settings and real datasets indicate that the proposed method is especially advantageous when the signal-to-noise ratio between significant features and irrelevant features is low.

Near-optimal Individualized Treatment Recommendations

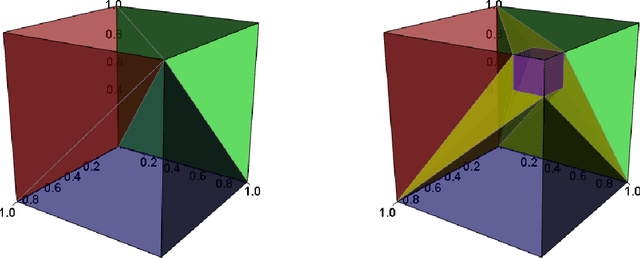
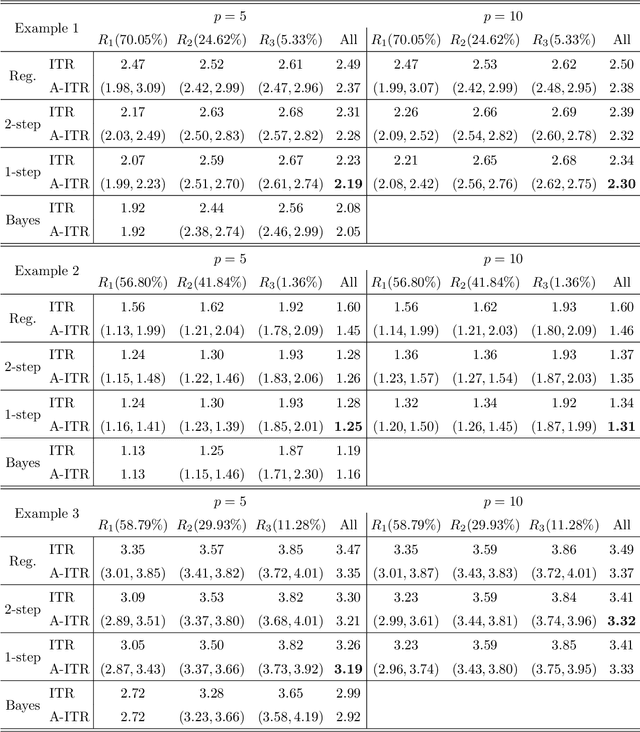
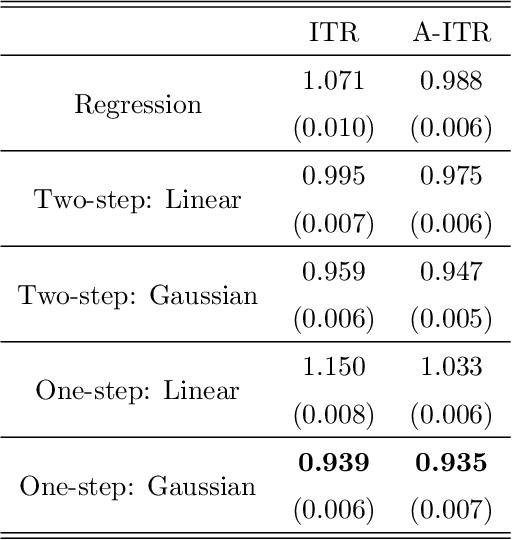
Individualized treatment recommendation (ITR) is an important analytic framework for precision medicine. The goal is to assign proper treatments to patients based on their individual characteristics. From the machine learning perspective, the solution to an ITR problem can be formulated as a weighted classification problem to maximize the average benefit that patients receive from the recommended treatments. Several methods have been proposed for ITR in both binary and multicategory treatment setups. In practice, one may prefer a more flexible recommendation with multiple treatment options. This motivates us to develop methods to obtain a set of near-optimal individualized treatment recommendations alternative to each other, called alternative individualized treatment recommendations (A-ITR). We propose two methods to estimate the optimal A-ITR within the outcome weighted learning (OWL) framework. We show the consistency of these methods and obtain an upper bound for the risk between the theoretically optimal recommendation and the estimated one. We also conduct simulation studies, and apply our methods to a real data set for Type 2 diabetic patients with injectable antidiabetic treatments. These numerical studies have shown the usefulness of the proposed A-ITR framework. We develop a R package aitr which can be found at https://github.com/menghaomiao/aitr.

Boosting Algorithms for Estimating Optimal Individualized Treatment Rules

We present nonparametric algorithms for estimating optimal individualized treatment rules. The proposed algorithms are based on the XGBoost algorithm, which is known as one of the most powerful algorithms in the machine learning literature. Our main idea is to model the conditional mean of clinical outcome or the decision rule via additive regression trees, and use the boosting technique to estimate each single tree iteratively. Our approaches overcome the challenge of correct model specification, which is required in current parametric methods. The major contribution of our proposed algorithms is providing efficient and accurate estimation of the highly nonlinear and complex optimal individualized treatment rules that often arise in practice. Finally, we illustrate the superior performance of our algorithms by extensive simulation studies and conclude with an application to the real data from a diabetes Phase III trial.

Multicategory Angle-based Learning for Estimating Optimal Dynamic Treatment Regimes with Censored Data

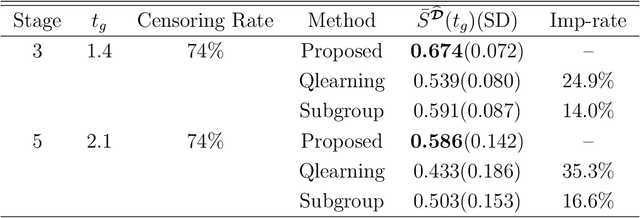
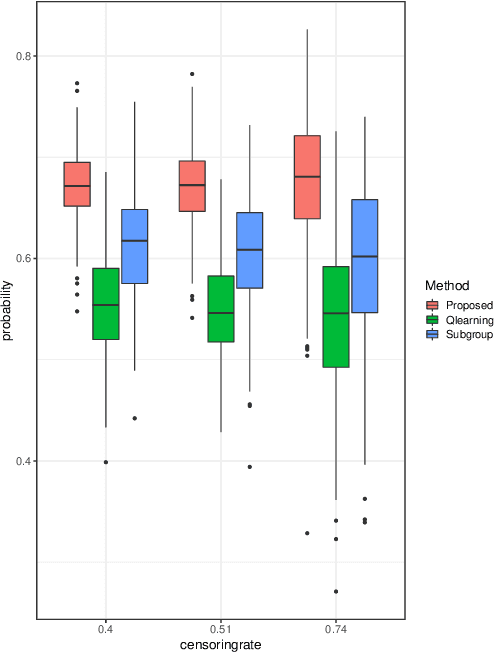
An optimal dynamic treatment regime (DTR) consists of a sequence of decision rules in maximizing long-term benefits, which is applicable for chronic diseases such as HIV infection or cancer. In this paper, we develop a novel angle-based approach to search the optimal DTR under a multicategory treatment framework for survival data. The proposed method targets maximization the conditional survival function of patients following a DTR. In contrast to most existing approaches which are designed to maximize the expected survival time under a binary treatment framework, the proposed method solves the multicategory treatment problem given multiple stages for censored data. Specifically, the proposed method obtains the optimal DTR via integrating estimations of decision rules at multiple stages into a single multicategory classification algorithm without imposing additional constraints, which is also more computationally efficient and robust. In theory, we establish Fisher consistency of the proposed method under regularity conditions. Our numerical studies show that the proposed method outperforms competing methods in terms of maximizing the conditional survival function. We apply the proposed method to two real datasets: Framingham heart study data and acquired immunodeficiency syndrome (AIDS) clinical data.