Multicategory Angle-based Learning for Estimating Optimal Dynamic Treatment Regimes with Censored Data
Paper and Code
Jan 14, 2020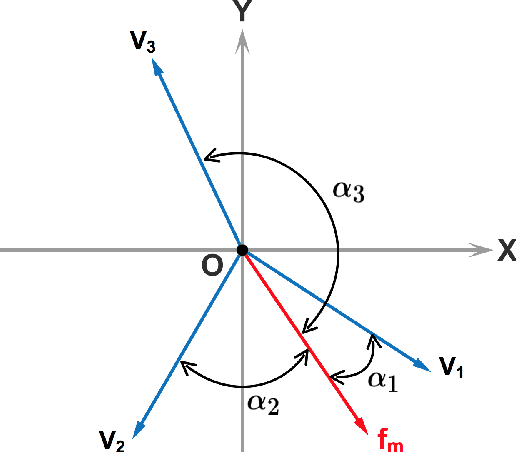
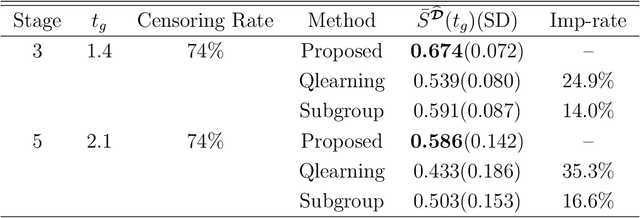
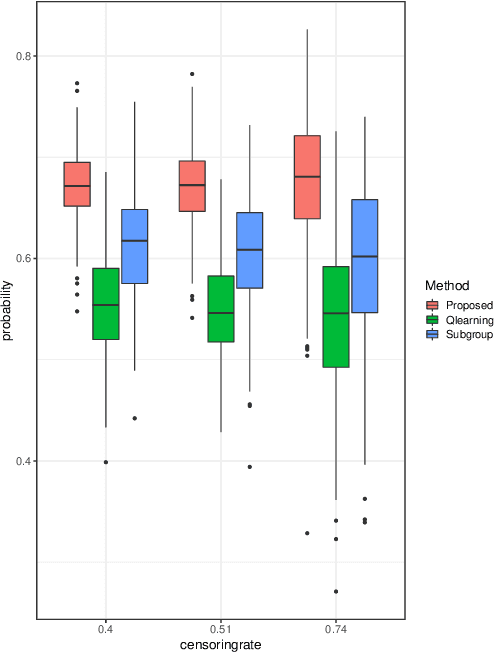

An optimal dynamic treatment regime (DTR) consists of a sequence of decision rules in maximizing long-term benefits, which is applicable for chronic diseases such as HIV infection or cancer. In this paper, we develop a novel angle-based approach to search the optimal DTR under a multicategory treatment framework for survival data. The proposed method targets maximization the conditional survival function of patients following a DTR. In contrast to most existing approaches which are designed to maximize the expected survival time under a binary treatment framework, the proposed method solves the multicategory treatment problem given multiple stages for censored data. Specifically, the proposed method obtains the optimal DTR via integrating estimations of decision rules at multiple stages into a single multicategory classification algorithm without imposing additional constraints, which is also more computationally efficient and robust. In theory, we establish Fisher consistency of the proposed method under regularity conditions. Our numerical studies show that the proposed method outperforms competing methods in terms of maximizing the conditional survival function. We apply the proposed method to two real datasets: Framingham heart study data and acquired immunodeficiency syndrome (AIDS) clinical data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge