An Efficient Quasi-Random Sampling for Copulas

This paper examines an efficient method for quasi-random sampling of copulas in Monte Carlo computations. Traditional methods, like conditional distribution methods (CDM), have limitations when dealing with high-dimensional or implicit copulas, which refer to those that cannot be accurately represented by existing parametric copulas. Instead, this paper proposes the use of generative models, such as Generative Adversarial Networks (GANs), to generate quasi-random samples for any copula. GANs are a type of implicit generative models used to learn the distribution of complex data, thus facilitating easy sampling. In our study, GANs are employed to learn the mapping from a uniform distribution to copulas. Once this mapping is learned, obtaining quasi-random samples from the copula only requires inputting quasi-random samples from the uniform distribution. This approach offers a more flexible method for any copula. Additionally, we provide theoretical analysis of quasi-Monte Carlo estimators based on quasi-random samples of copulas. Through simulated and practical applications, particularly in the field of risk management, we validate the proposed method and demonstrate its superiority over various existing methods.

Fast Approximation of the Shapley Values Based on Order-of-Addition Experimental Designs

Shapley value is originally a concept in econometrics to fairly distribute both gains and costs to players in a coalition game. In the recent decades, its application has been extended to other areas such as marketing, engineering and machine learning. For example, it produces reasonable solutions for problems in sensitivity analysis, local model explanation towards the interpretable machine learning, node importance in social network, attribution models, etc. However, its heavy computational burden has been long recognized but rarely investigated. Specifically, in a $d$-player coalition game, calculating a Shapley value requires the evaluation of $d!$ or $2^d$ marginal contribution values, depending on whether we are taking the permutation or combination formulation of the Shapley value. Hence it becomes infeasible to calculate the Shapley value when $d$ is reasonably large. A common remedy is to take a random sample of the permutations to surrogate for the complete list of permutations. We find an advanced sampling scheme can be designed to yield much more accurate estimation of the Shapley value than the simple random sampling (SRS). Our sampling scheme is based on combinatorial structures in the field of design of experiments (DOE), particularly the order-of-addition experimental designs for the study of how the orderings of components would affect the output. We show that the obtained estimates are unbiased, and can sometimes deterministically recover the original Shapley value. Both theoretical and simulations results show that our DOE-based sampling scheme outperforms SRS in terms of estimation accuracy. Surprisingly, it is also slightly faster than SRS. Lastly, real data analysis is conducted for the C. elegans nervous system and the 9/11 terrorist network.

Towards Long-Tailed Recognition for Graph Classification via Collaborative Experts

Graph classification, aiming at learning the graph-level representations for effective class assignments, has received outstanding achievements, which heavily relies on high-quality datasets that have balanced class distribution. In fact, most real-world graph data naturally presents a long-tailed form, where the head classes occupy much more samples than the tail classes, it thus is essential to study the graph-level classification over long-tailed data while still remaining largely unexplored. However, most existing long-tailed learning methods in visions fail to jointly optimize the representation learning and classifier training, as well as neglect the mining of the hard-to-classify classes. Directly applying existing methods to graphs may lead to sub-optimal performance, since the model trained on graphs would be more sensitive to the long-tailed distribution due to the complex topological characteristics. Hence, in this paper, we propose a novel long-tailed graph-level classification framework via Collaborative Multi-expert Learning (CoMe) to tackle the problem. To equilibrate the contributions of head and tail classes, we first develop balanced contrastive learning from the view of representation learning, and then design an individual-expert classifier training based on hard class mining. In addition, we execute gated fusion and disentangled knowledge distillation among the multiple experts to promote the collaboration in a multi-expert framework. Comprehensive experiments are performed on seven widely-used benchmark datasets to demonstrate the superiority of our method CoMe over state-of-the-art baselines.

Model-free Subsampling Method Based on Uniform Designs

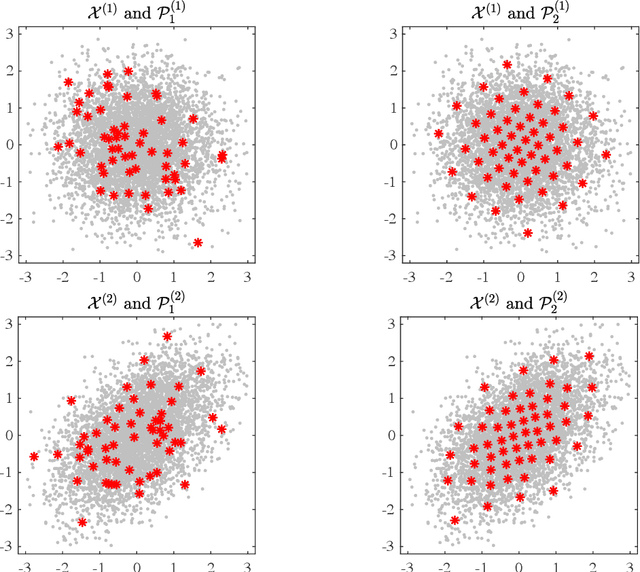
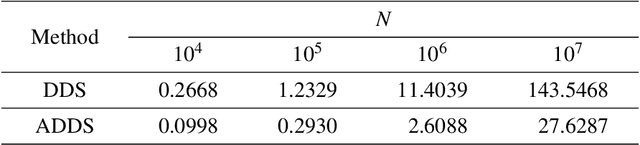
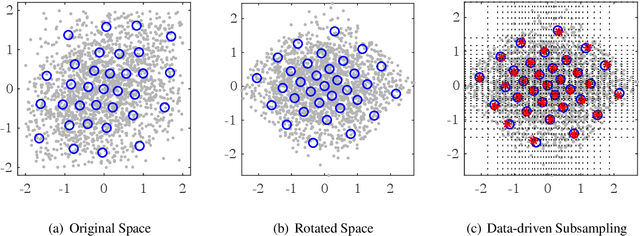
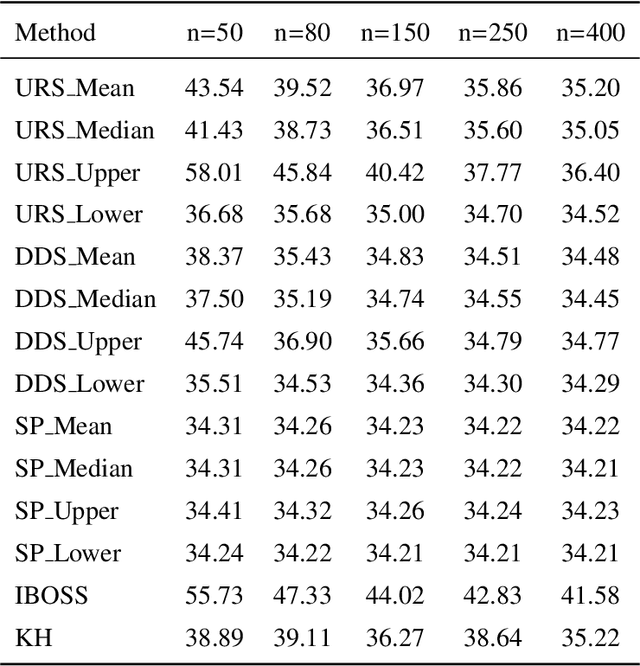
Subsampling or subdata selection is a useful approach in large-scale statistical learning. Most existing studies focus on model-based subsampling methods which significantly depend on the model assumption. In this paper, we consider the model-free subsampling strategy for generating subdata from the original full data. In order to measure the goodness of representation of a subdata with respect to the original data, we propose a criterion, generalized empirical F-discrepancy (GEFD), and study its theoretical properties in connection with the classical generalized L2-discrepancy in the theory of uniform designs. These properties allow us to develop a kind of low-GEFD data-driven subsampling method based on the existing uniform designs. By simulation examples and a real case study, we show that the proposed subsampling method is superior to the random sampling method. Moreover, our method keeps robust under diverse model specifications while other popular subsampling methods are under-performing. In practice, such a model-free property is more appealing than the model-based subsampling methods, where the latter may have poor performance when the model is misspecified, as demonstrated in our simulation studies.