Regularized Training and Tight Certification for Randomized Smoothed Classifier with Provable Robustness

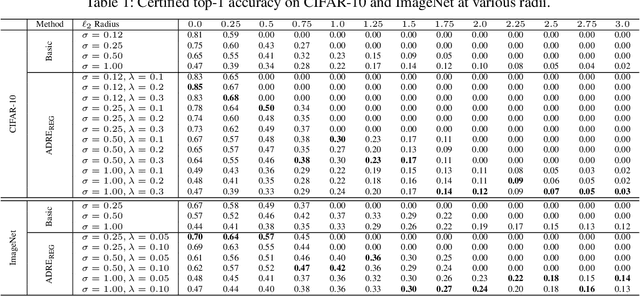
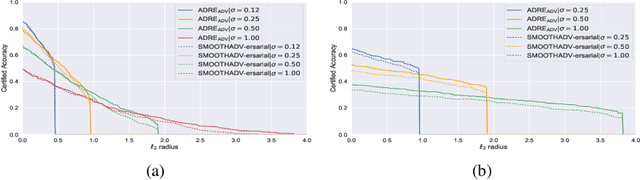
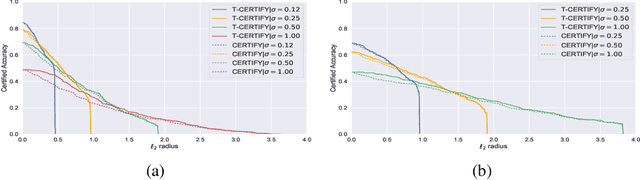
Recently smoothing deep neural network based classifiers via isotropic Gaussian perturbation is shown to be an effective and scalable way to provide state-of-the-art probabilistic robustness guarantee against $\ell_2$ norm bounded adversarial perturbations. However, how to train a good base classifier that is accurate and robust when smoothed has not been fully investigated. In this work, we derive a new regularized risk, in which the regularizer can adaptively encourage the accuracy and robustness of the smoothed counterpart when training the base classifier. It is computationally efficient and can be implemented in parallel with other empirical defense methods. We discuss how to implement it under both standard (non-adversarial) and adversarial training scheme. At the same time, we also design a new certification algorithm, which can leverage the regularization effect to provide tighter robustness lower bound that holds with high probability. Our extensive experimentation demonstrates the effectiveness of the proposed training and certification approaches on CIFAR-10 and ImageNet datasets.

Nonregular and Minimax Estimation of Individualized Thresholds in High Dimension with Binary Responses

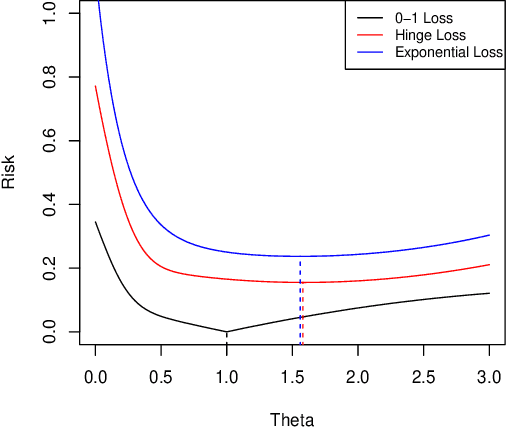
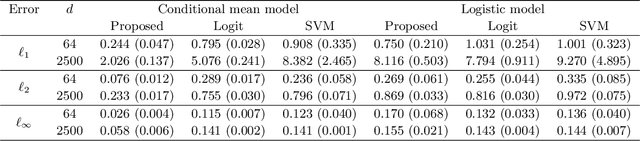
Given a large number of covariates $Z$, we consider the estimation of a high-dimensional parameter $\theta$ in an individualized linear threshold $\theta^T Z$ for a continuous variable $X$, which minimizes the disagreement between $\text{sign}(X-\theta^TZ)$ and a binary response $Y$. While the problem can be formulated into the M-estimation framework, minimizing the corresponding empirical risk function is computationally intractable due to discontinuity of the sign function. Moreover, estimating $\theta$ even in the fixed-dimensional setting is known as a nonregular problem leading to nonstandard asymptotic theory. To tackle the computational and theoretical challenges in the estimation of the high-dimensional parameter $\theta$, we propose an empirical risk minimization approach based on a regularized smoothed loss function. The statistical and computational trade-off of the algorithm is investigated. Statistically, we show that the finite sample error bound for estimating $\theta$ in $\ell_2$ norm is $(s\log d/n)^{\beta/(2\beta+1)}$, where $d$ is the dimension of $\theta$, $s$ is the sparsity level, $n$ is the sample size and $\beta$ is the smoothness of the conditional density of $X$ given the response $Y$ and the covariates $Z$. The convergence rate is nonstandard and slower than that in the classical Lasso problems. Furthermore, we prove that the resulting estimator is minimax rate optimal up to a logarithmic factor. The Lepski's method is developed to achieve the adaption to the unknown sparsity $s$ and smoothness $\beta$. Computationally, an efficient path-following algorithm is proposed to compute the solution path. We show that this algorithm achieves geometric rate of convergence for computing the whole path. Finally, we evaluate the finite sample performance of the proposed estimator in simulation studies and a real data analysis.