Treatment Effect Estimation with Unobserved and Heterogeneous Confounding Variables
Paper and Code
Jul 29, 2022
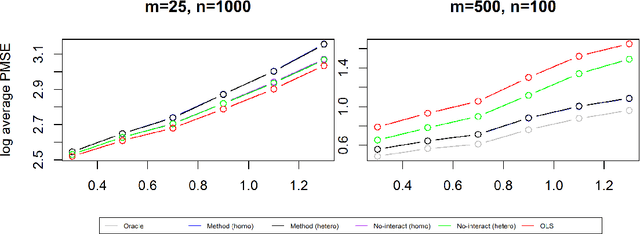


The estimation of the treatment effect is often biased in the presence of unobserved confounding variables which are commonly referred to as hidden variables. Although a few methods have been recently proposed to handle the effect of hidden variables, these methods often overlook the possibility of any interaction between the observed treatment variable and the unobserved covariates. In this work, we address this shortcoming by studying a multivariate response regression problem with both unobserved and heterogeneous confounding variables of the form $Y=A^T X+ B^T Z+ \sum_{j=1}^{p} C^T_j X_j Z + E$, where $Y \in \mathbb{R}^m$ are $m$-dimensional response variables, $X \in \mathbb{R}^p$ are observed covariates (including the treatment variable), $Z \in \mathbb{R}^K$ are $K$-dimensional unobserved confounders, and $E \in \mathbb{R}^m$ is the random noise. Allowing for the interaction between $X_j$ and $Z$ induces the heterogeneous confounding effect. Our goal is to estimate the unknown matrix $A$, the direct effect of the observed covariates or the treatment on the responses. To this end, we propose a new debiased estimation approach via SVD to remove the effect of unobserved confounding variables. The rate of convergence of the estimator is established under both the homoscedastic and heteroscedastic noises. We also present several simulation experiments and a real-world data application to substantiate our findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge