Kernel Ridge Regression via Partitioning
Paper and Code
Aug 05, 2016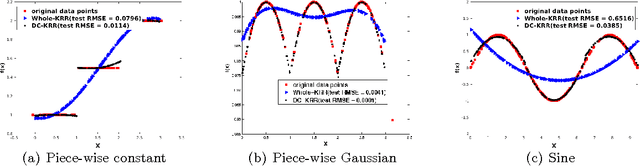
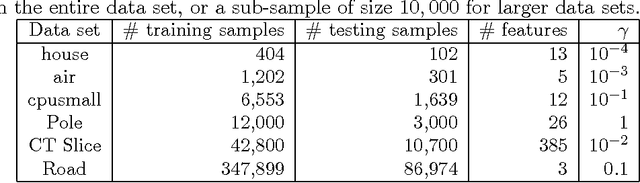
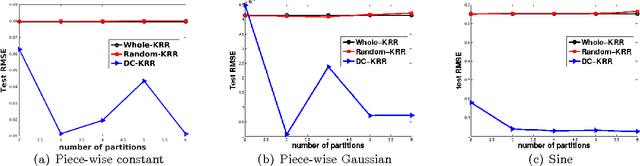

In this paper, we investigate a divide and conquer approach to Kernel Ridge Regression (KRR). Given n samples, the division step involves separating the points based on some underlying disjoint partition of the input space (possibly via clustering), and then computing a KRR estimate for each partition. The conquering step is simple: for each partition, we only consider its own local estimate for prediction. We establish conditions under which we can give generalization bounds for this estimator, as well as achieve optimal minimax rates. We also show that the approximation error component of the generalization error is lesser than when a single KRR estimate is fit on the data: thus providing both statistical and computational advantages over a single KRR estimate over the entire data (or an averaging over random partitions as in other recent work, [30]). Lastly, we provide experimental validation for our proposed estimator and our assumptions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge