Beyond PCA: A Probabilistic Gram-Schmidt Approach to Feature Extraction
Paper and Code
Nov 15, 2023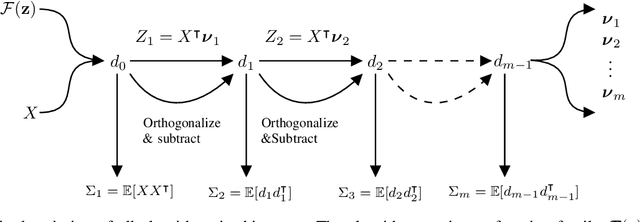


Linear feature extraction at the presence of nonlinear dependencies among the data is a fundamental challenge in unsupervised learning. We propose using a Probabilistic Gram-Schmidt (PGS) type orthogonalization process in order to detect and map out redundant dimensions. Specifically, by applying the PGS process over any family of functions which presumably captures the nonlinear dependencies in the data, we construct a series of covariance matrices that can either be used to remove those dependencies from the principal components, or to identify new large-variance directions. In the former case, we prove that under certain assumptions the resulting algorithms detect and remove nonlinear dependencies whenever those dependencies lie in the linear span of the chosen function family. In the latter, we provide information-theoretic guarantees in terms of entropy reduction. Both proposed methods extract linear features from the data while removing nonlinear redundancies. We provide simulation results on synthetic and real-world datasets which show improved performance over PCA and state-of-the-art linear feature extraction algorithms, both in terms of variance maximization of the extracted features, and in terms of improved performance of classification algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge