Lagrange Coded Computing: Optimal Design for Resiliency, Security and Privacy

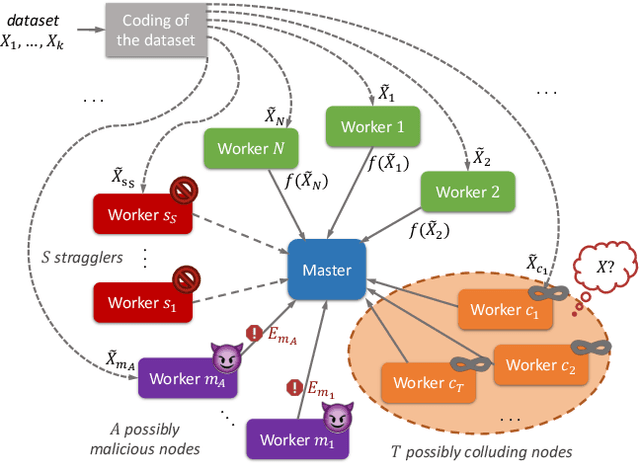
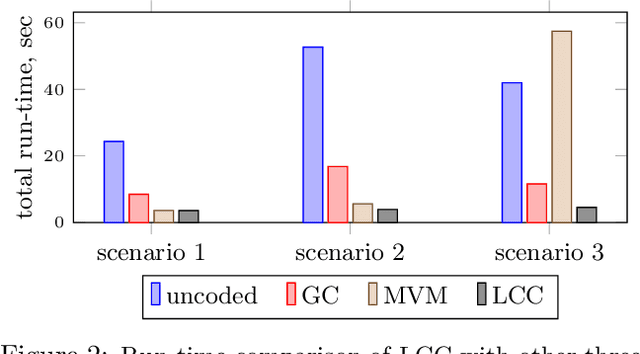
We consider a distributed computing scenario that involves computations over a massive dataset that is stored distributedly across multiple workers. We propose Lagrange Coded Computing, a new framework to simultaneously provide (1) resiliency against straggler workers that may prolong computations; (2) security against Byzantine (or malicious) workers that deliberately modify the computation for their benefit; and (3) (information-theoretic) privacy of the dataset amidst possible collusion of workers. Lagrange Coded Computing, which leverages the well-known Lagrange polynomial to create computation redundancy in a novel coded form across the workers, can be applied to any computation scenario in which the function of interest is an arbitrary multivariate polynomial of the input dataset, hence covering many computations of interest in machine learning. Lagrange Coded Computing significantly generalizes prior works to go beyond linear computations that have so far been the main focus in this area. We prove the optimality of Lagrange Coded Computing by developing matching converses, and empirically demonstrate its impact in mitigating stragglers and malicious workers.