Secure Aggregation for Buffered Asynchronous Federated Learning

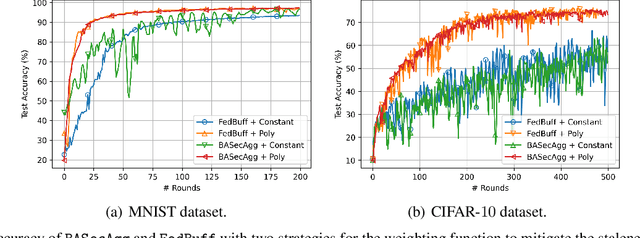
Federated learning (FL) typically relies on synchronous training, which is slow due to stragglers. While asynchronous training handles stragglers efficiently, it does not ensure privacy due to the incompatibility with the secure aggregation protocols. A buffered asynchronous training protocol known as FedBuff has been proposed recently which bridges the gap between synchronous and asynchronous training to mitigate stragglers and to also ensure privacy simultaneously. FedBuff allows the users to send their updates asynchronously while ensuring privacy by storing the updates in a trusted execution environment (TEE) enabled private buffer. TEEs, however, have limited memory which limits the buffer size. Motivated by this limitation, we develop a buffered asynchronous secure aggregation (BASecAgg) protocol that does not rely on TEEs. The conventional secure aggregation protocols cannot be applied in the buffered asynchronous setting since the buffer may have local models corresponding to different rounds and hence the masks that the users use to protect their models may not cancel out. BASecAgg addresses this challenge by carefully designing the masks such that they cancel out even if they correspond to different rounds. Our convergence analysis and experiments show that BASecAgg almost has the same convergence guarantees as FedBuff without relying on TEEs.

ApproxIFER: A Model-Agnostic Approach to Resilient and Robust Prediction Serving Systems

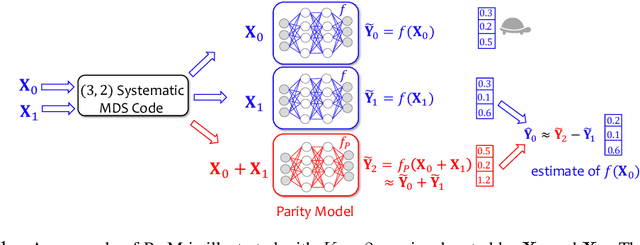
Due to the surge of cloud-assisted AI services, the problem of designing resilient prediction serving systems that can effectively cope with stragglers/failures and minimize response delays has attracted much interest. The common approach for tackling this problem is replication which assigns the same prediction task to multiple workers. This approach, however, is very inefficient and incurs significant resource overheads. Hence, a learning-based approach known as parity model (ParM) has been recently proposed which learns models that can generate parities for a group of predictions in order to reconstruct the predictions of the slow/failed workers. While this learning-based approach is more resource-efficient than replication, it is tailored to the specific model hosted by the cloud and is particularly suitable for a small number of queries (typically less than four) and tolerating very few (mostly one) number of stragglers. Moreover, ParM does not handle Byzantine adversarial workers. We propose a different approach, named Approximate Coded Inference (ApproxIFER), that does not require training of any parity models, hence it is agnostic to the model hosted by the cloud and can be readily applied to different data domains and model architectures. Compared with earlier works, ApproxIFER can handle a general number of stragglers and scales significantly better with the number of queries. Furthermore, ApproxIFER is robust against Byzantine workers. Our extensive experiments on a large number of datasets and model architectures also show significant accuracy improvement by up to 58% over the parity model approaches.

List-Decodable Coded Computing: Breaking the Adversarial Toleration Barrier

We consider the problem of coded computing where a computational task is performed in a distributed fashion in the presence of adversarial workers. We propose techniques to break the adversarial toleration threshold barrier previously known in coded computing. More specifically, we leverage list-decoding techniques for folded Reed-Solomon (FRS) codes and propose novel algorithms to recover the correct codeword using side information. In the coded computing setting, we show how the master node can perform certain carefully designed extra computations in order to obtain the side information. This side information will be then utilized to prune the output of list decoder in order to uniquely recover the true outcome. We further propose folded Lagrange coded computing, referred to as folded LCC or FLCC, to incorporate the developed techniques into a specific coded computing setting. Our results show that FLCC outperforms LCC by breaking the barrier on the number of adversaries that can be tolerated. In particular, the corresponding threshold in FLCC is improved by a factor of two compared to that of LCC.

On Polynomial Approximations for Privacy-Preserving and Verifiable ReLU Networks

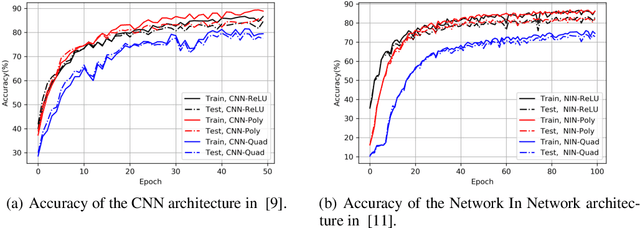
Outsourcing neural network inference tasks to an untrusted cloud raises data privacy and integrity concerns. In order to address these challenges, several privacy-preserving and verifiable inference techniques have been proposed based on replacing the non-polynomial activation functions such as the rectified linear unit (ReLU) function with polynomial activation functions. Such techniques usually require the polynomial coefficients to be in a finite field. Motivated by such requirements, several works proposed replacing the ReLU activation function with the square activation function. In this work, we empirically show that the square function is not the best second-degree polynomial that can replace the ReLU function in deep neural networks. We instead propose a second-degree polynomial activation function with a first order term and empirically show that it can lead to much better models. Our experiments on the CIFAR-$10$ dataset show that our proposed polynomial activation function significantly outperforms the square activation function.

A Scalable Approach for Privacy-Preserving Collaborative Machine Learning

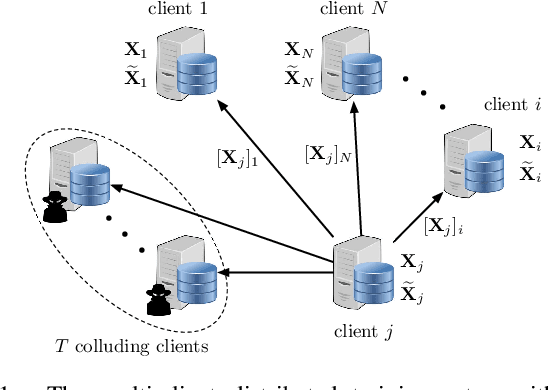
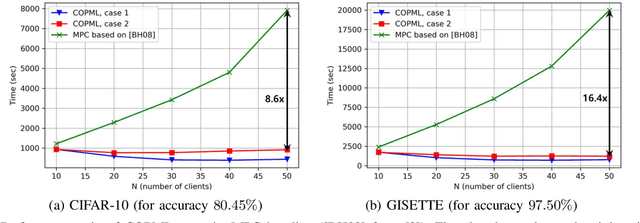
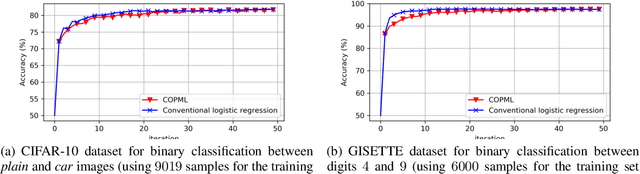
We consider a collaborative learning scenario in which multiple data-owners wish to jointly train a logistic regression model, while keeping their individual datasets private from the other parties. We propose COPML, a fully-decentralized training framework that achieves scalability and privacy-protection simultaneously. The key idea of COPML is to securely encode the individual datasets to distribute the computation load effectively across many parties and to perform the training computations as well as the model updates in a distributed manner on the securely encoded data. We provide the privacy analysis of COPML and prove its convergence. Furthermore, we experimentally demonstrate that COPML can achieve significant speedup in training over the benchmark protocols. Our protocol provides strong statistical privacy guarantees against colluding parties (adversaries) with unbounded computational power, while achieving up to $16\times$ speedup in the training time against the benchmark protocols.

Analog Lagrange Coded Computing

A distributed computing scenario is considered, where the computational power of a set of worker nodes is used to perform a certain computation task over a dataset that is dispersed among the workers. Lagrange coded computing (LCC), proposed by Yu et al., leverages the well-known Lagrange polynomial to perform polynomial evaluation of the dataset in such a scenario in an efficient parallel fashion while keeping the privacy of data amidst possible collusion of workers. This solution relies on quantizing the data into a finite field, so that Shamir's secret sharing, as one of its main building blocks, can be employed. Such a solution, however, is not properly scalable with the size of dataset, mainly due to computation overflows. To address such a critical issue, we propose a novel extension of LCC to the analog domain, referred to as analog LCC (ALCC). All the operations in the proposed ALCC protocol are done over the infinite fields of R/C but for practical implementations floating-point numbers are used. We characterize the privacy of data in ALCC, against any subset of colluding workers up to a certain size, in terms of the distinguishing security (DS) and the mutual information security (MIS) metrics. Also, the accuracy of outcome is characterized in a practical setting assuming operations are performed using floating-point numbers. Consequently, a fundamental trade-off between the accuracy of the outcome of ALCC and its privacy level is observed and is numerically evaluated. Moreover, we implement the proposed scheme to perform matrix-matrix multiplication over a batch of matrices. It is observed that ALCC is superior compared to the state-of-the-art LCC, implemented using fixed-point numbers, assuming both schemes use an equal number of bits to represent data symbols.

Byzantine-Resilient Secure Federated Learning

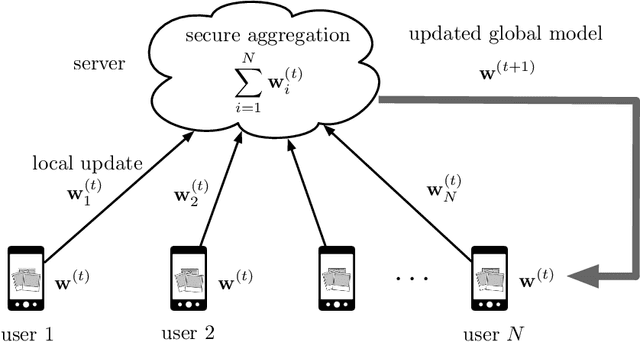
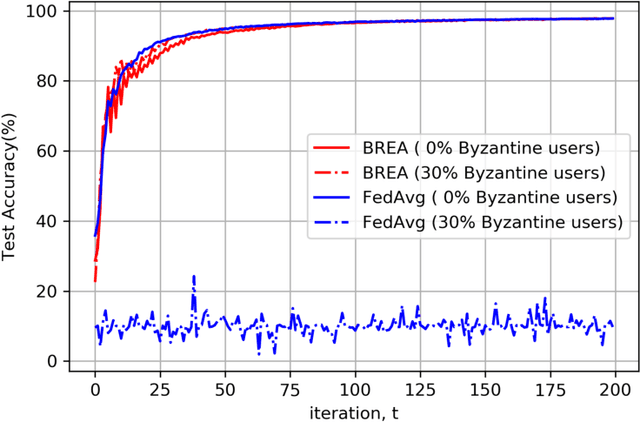
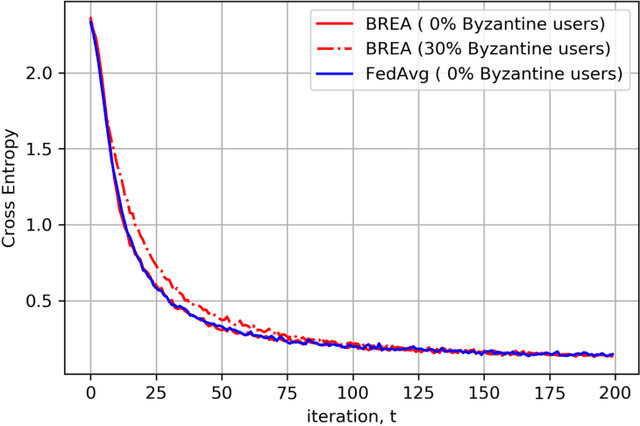
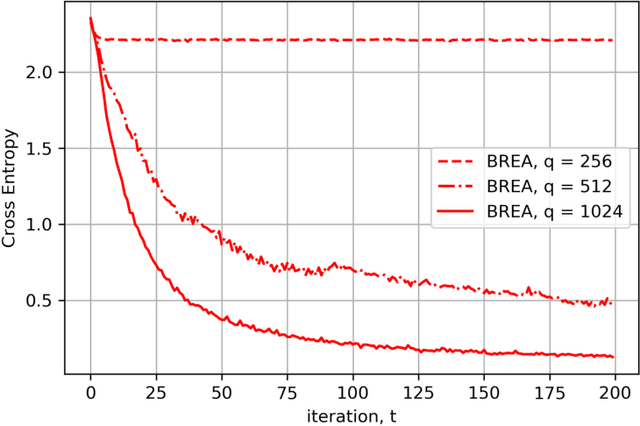
Secure federated learning is a privacy-preserving framework to improve machine learning models by training over large volumes of data collected by mobile users. This is achieved through an iterative process where, at each iteration, users update a global model using their local datasets. Each user then masks its local model via random keys, and the masked models are aggregated at a central server to compute the global model for the next iteration. As the local models are protected by random masks, the server cannot observe their true values. This presents a major challenge for the resilience of the model against adversarial (Byzantine) users, who can manipulate the global model by modifying their local models or datasets. Towards addressing this challenge, this paper presents the first single-server Byzantine-resilient secure aggregation framework (BREA) for secure federated learning. BREA is based on an integrated stochastic quantization, verifiable outlier detection, and secure model aggregation approach to guarantee Byzantine-resilience, privacy, and convergence simultaneously. We provide theoretical convergence and privacy guarantees and characterize the fundamental trade-offs in terms of the network size, user dropouts, and privacy protection. Our experiments demonstrate convergence in the presence of Byzantine users, and comparable accuracy to conventional federated learning benchmarks.

Privacy-Preserving Distributed Learning in the Analog Domain

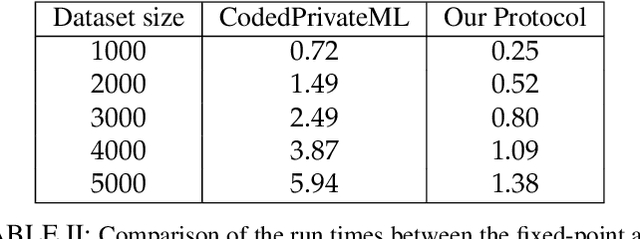
We consider the critical problem of distributed learning over data while keeping it private from the computational servers. The state-of-the-art approaches to this problem rely on quantizing the data into a finite field, so that the cryptographic approaches for secure multiparty computing can then be employed. These approaches, however, can result in substantial accuracy losses due to fixed-point representation of the data and computation overflows. To address these critical issues, we propose a novel algorithm to solve the problem when data is in the analog domain, e.g., the field of real/complex numbers. We characterize the privacy of the data from both information-theoretic and cryptographic perspectives, while establishing a connection between the two notions in the analog domain. More specifically, the well-known connection between the distinguishing security (DS) and the mutual information security (MIS) metrics is extended from the discrete domain to the continues domain. This is then utilized to bound the amount of information about the data leaked to the servers in our protocol, in terms of the DS metric, using well-known results on the capacity of single-input multiple-output (SIMO) channel with correlated noise. It is shown how the proposed framework can be adopted to do computation tasks when data is represented using floating-point numbers. We then show that this leads to a fundamental trade-off between the privacy level of data and accuracy of the result. As an application, we also show how to train a machine learning model while keeping the data as well as the trained model private. Then numerical results are shown for experiments on the MNIST dataset. Furthermore, experimental advantages are shown comparing to fixed-point implementations over finite fields.

Coded Computing for Federated Learning at the Edge

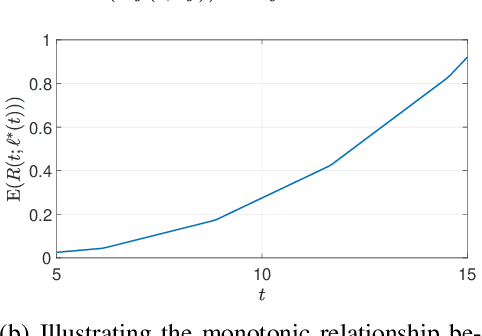
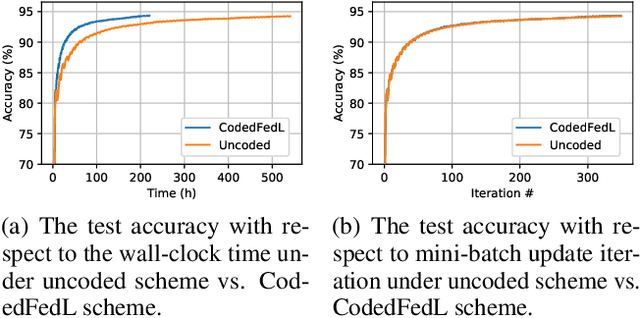
Federated Learning (FL) is an exciting new paradigm that enables training a global model from data generated locally at the client nodes, without moving client data to a centralized server. Performance of FL in a multi-access edge computing (MEC) network suffers from slow convergence due to heterogeneity and stochastic fluctuations in compute power and communication link qualities across clients. A recent work, Coded Federated Learning (CFL), proposes to mitigate stragglers and speed up training for linear regression tasks by assigning redundant computations at the MEC server. Coding redundancy in CFL is computed by exploiting statistical properties of compute and communication delays. We develop CodedFedL that addresses the difficult task of extending CFL to distributed non-linear regression and classification problems with multioutput labels. The key innovation of our work is to exploit distributed kernel embedding using random Fourier features that transforms the training task into distributed linear regression. We provide an analytical solution for load allocation, and demonstrate significant performance gains for CodedFedL through experiments over benchmark datasets using practical network parameters.

Minimax Lower Bounds for Transfer Learning with Linear and One-hidden Layer Neural Networks

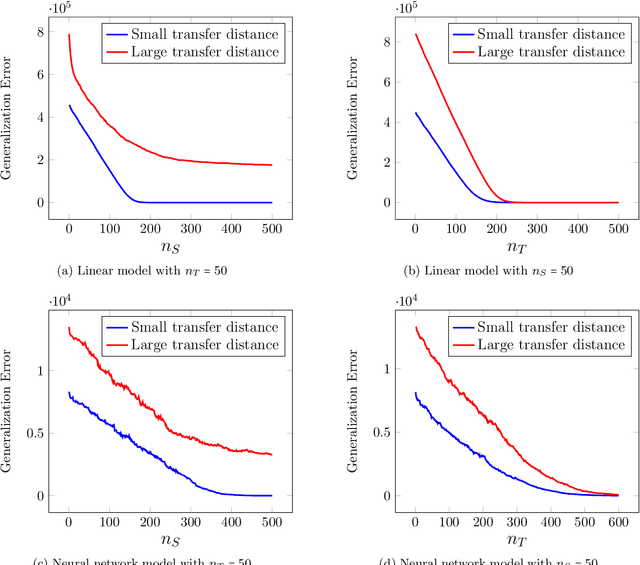
Transfer learning has emerged as a powerful technique for improving the performance of machine learning models on new domains where labeled training data may be scarce. In this approach a model trained for a source task, where plenty of labeled training data is available, is used as a starting point for training a model on a related target task with only few labeled training data. Despite recent empirical success of transfer learning approaches, the benefits and fundamental limits of transfer learning are poorly understood. In this paper we develop a statistical minimax framework to characterize the fundamental limits of transfer learning in the context of regression with linear and one-hidden layer neural network models. Specifically, we derive a lower-bound for the target generalization error achievable by any algorithm as a function of the number of labeled source and target data as well as appropriate notions of similarity between the source and target tasks. Our lower bound provides new insights into the benefits and limitations of transfer learning. We further corroborate our theoretical finding with various experiments.