ApproxIFER: A Model-Agnostic Approach to Resilient and Robust Prediction Serving Systems

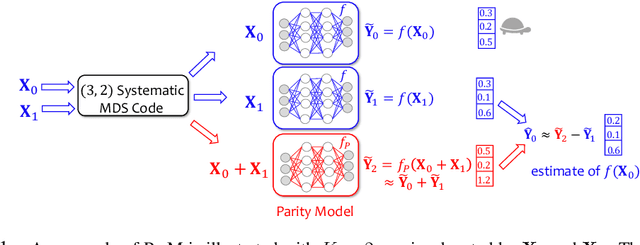
Due to the surge of cloud-assisted AI services, the problem of designing resilient prediction serving systems that can effectively cope with stragglers/failures and minimize response delays has attracted much interest. The common approach for tackling this problem is replication which assigns the same prediction task to multiple workers. This approach, however, is very inefficient and incurs significant resource overheads. Hence, a learning-based approach known as parity model (ParM) has been recently proposed which learns models that can generate parities for a group of predictions in order to reconstruct the predictions of the slow/failed workers. While this learning-based approach is more resource-efficient than replication, it is tailored to the specific model hosted by the cloud and is particularly suitable for a small number of queries (typically less than four) and tolerating very few (mostly one) number of stragglers. Moreover, ParM does not handle Byzantine adversarial workers. We propose a different approach, named Approximate Coded Inference (ApproxIFER), that does not require training of any parity models, hence it is agnostic to the model hosted by the cloud and can be readily applied to different data domains and model architectures. Compared with earlier works, ApproxIFER can handle a general number of stragglers and scales significantly better with the number of queries. Furthermore, ApproxIFER is robust against Byzantine workers. Our extensive experiments on a large number of datasets and model architectures also show significant accuracy improvement by up to 58% over the parity model approaches.

List-Decodable Coded Computing: Breaking the Adversarial Toleration Barrier

We consider the problem of coded computing where a computational task is performed in a distributed fashion in the presence of adversarial workers. We propose techniques to break the adversarial toleration threshold barrier previously known in coded computing. More specifically, we leverage list-decoding techniques for folded Reed-Solomon (FRS) codes and propose novel algorithms to recover the correct codeword using side information. In the coded computing setting, we show how the master node can perform certain carefully designed extra computations in order to obtain the side information. This side information will be then utilized to prune the output of list decoder in order to uniquely recover the true outcome. We further propose folded Lagrange coded computing, referred to as folded LCC or FLCC, to incorporate the developed techniques into a specific coded computing setting. Our results show that FLCC outperforms LCC by breaking the barrier on the number of adversaries that can be tolerated. In particular, the corresponding threshold in FLCC is improved by a factor of two compared to that of LCC.

Analog Lagrange Coded Computing

A distributed computing scenario is considered, where the computational power of a set of worker nodes is used to perform a certain computation task over a dataset that is dispersed among the workers. Lagrange coded computing (LCC), proposed by Yu et al., leverages the well-known Lagrange polynomial to perform polynomial evaluation of the dataset in such a scenario in an efficient parallel fashion while keeping the privacy of data amidst possible collusion of workers. This solution relies on quantizing the data into a finite field, so that Shamir's secret sharing, as one of its main building blocks, can be employed. Such a solution, however, is not properly scalable with the size of dataset, mainly due to computation overflows. To address such a critical issue, we propose a novel extension of LCC to the analog domain, referred to as analog LCC (ALCC). All the operations in the proposed ALCC protocol are done over the infinite fields of R/C but for practical implementations floating-point numbers are used. We characterize the privacy of data in ALCC, against any subset of colluding workers up to a certain size, in terms of the distinguishing security (DS) and the mutual information security (MIS) metrics. Also, the accuracy of outcome is characterized in a practical setting assuming operations are performed using floating-point numbers. Consequently, a fundamental trade-off between the accuracy of the outcome of ALCC and its privacy level is observed and is numerically evaluated. Moreover, we implement the proposed scheme to perform matrix-matrix multiplication over a batch of matrices. It is observed that ALCC is superior compared to the state-of-the-art LCC, implemented using fixed-point numbers, assuming both schemes use an equal number of bits to represent data symbols.

Privacy-Preserving Distributed Learning in the Analog Domain

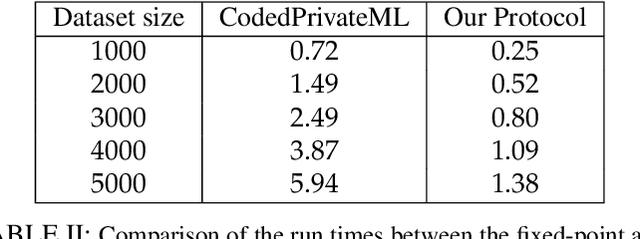
We consider the critical problem of distributed learning over data while keeping it private from the computational servers. The state-of-the-art approaches to this problem rely on quantizing the data into a finite field, so that the cryptographic approaches for secure multiparty computing can then be employed. These approaches, however, can result in substantial accuracy losses due to fixed-point representation of the data and computation overflows. To address these critical issues, we propose a novel algorithm to solve the problem when data is in the analog domain, e.g., the field of real/complex numbers. We characterize the privacy of the data from both information-theoretic and cryptographic perspectives, while establishing a connection between the two notions in the analog domain. More specifically, the well-known connection between the distinguishing security (DS) and the mutual information security (MIS) metrics is extended from the discrete domain to the continues domain. This is then utilized to bound the amount of information about the data leaked to the servers in our protocol, in terms of the DS metric, using well-known results on the capacity of single-input multiple-output (SIMO) channel with correlated noise. It is shown how the proposed framework can be adopted to do computation tasks when data is represented using floating-point numbers. We then show that this leads to a fundamental trade-off between the privacy level of data and accuracy of the result. As an application, we also show how to train a machine learning model while keeping the data as well as the trained model private. Then numerical results are shown for experiments on the MNIST dataset. Furthermore, experimental advantages are shown comparing to fixed-point implementations over finite fields.