Minimax Lower Bounds for Transfer Learning with Linear and One-hidden Layer Neural Networks

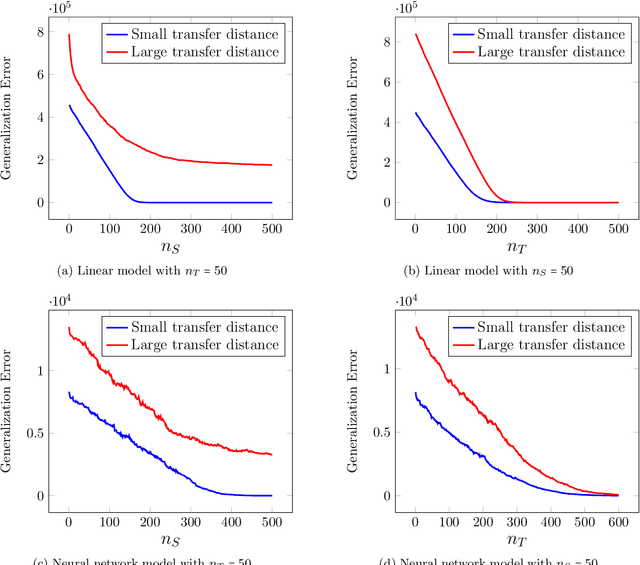
Transfer learning has emerged as a powerful technique for improving the performance of machine learning models on new domains where labeled training data may be scarce. In this approach a model trained for a source task, where plenty of labeled training data is available, is used as a starting point for training a model on a related target task with only few labeled training data. Despite recent empirical success of transfer learning approaches, the benefits and fundamental limits of transfer learning are poorly understood. In this paper we develop a statistical minimax framework to characterize the fundamental limits of transfer learning in the context of regression with linear and one-hidden layer neural network models. Specifically, we derive a lower-bound for the target generalization error achievable by any algorithm as a function of the number of labeled source and target data as well as appropriate notions of similarity between the source and target tasks. Our lower bound provides new insights into the benefits and limitations of transfer learning. We further corroborate our theoretical finding with various experiments.

Fitting ReLUs via SGD and Quantized SGD

In this paper we focus on the problem of finding the optimal weights of the shallowest of neural networks consisting of a single Rectified Linear Unit (ReLU). These functions are of the form $\mathbf{x}\rightarrow \max(0,\langle\mathbf{w},\mathbf{x}\rangle)$ with $\mathbf{w}\in\mathbb{R}^d$ denoting the weight vector. We focus on a planted model where the inputs are chosen i.i.d. from a Gaussian distribution and the labels are generated according to a planted weight vector. We first show that mini-batch stochastic gradient descent when suitably initialized, converges at a geometric rate to the planted model with a number of samples that is optimal up to numerical constants. Next we focus on a parallel implementation where in each iteration the mini-batch gradient is calculated in a distributed manner across multiple processors and then broadcast to a master or all other processors. To reduce the communication cost in this setting we utilize a Quanitzed Stochastic Gradient Scheme (QSGD) where the partial gradients are quantized. Perhaps unexpectedly, we show that QSGD maintains the fast convergence of SGD to a globally optimal model while significantly reducing the communication cost. We further corroborate our numerical findings via various experiments including distributed implementations over Amazon EC2.

Polynomially Coded Regression: Optimal Straggler Mitigation via Data Encoding

We consider the problem of training a least-squares regression model on a large dataset using gradient descent. The computation is carried out on a distributed system consisting of a master node and multiple worker nodes. Such distributed systems are significantly slowed down due to the presence of slow-running machines (stragglers) as well as various communication bottlenecks. We propose "polynomially coded regression" (PCR) that substantially reduces the effect of stragglers and lessens the communication burden in such systems. The key idea of PCR is to encode the partial data stored at each worker, such that the computations at the workers can be viewed as evaluating a polynomial at distinct points. This allows the master to compute the final gradient by interpolating this polynomial. PCR significantly reduces the recovery threshold, defined as the number of workers the master has to wait for prior to computing the gradient. In particular, PCR requires a recovery threshold that scales inversely proportionally with the amount of computation/storage available at each worker. In comparison, state-of-the-art straggler-mitigation schemes require a much higher recovery threshold that only decreases linearly in the per worker computation/storage load. We prove that PCR's recovery threshold is near minimal and within a factor two of the best possible scheme. Our experiments over Amazon EC2 demonstrate that compared with state-of-the-art schemes, PCR improves the run-time by 1.50x ~ 2.36x with naturally occurring stragglers, and by as much as 2.58x ~ 4.29x with artificial stragglers.

Fundamental Resource Trade-offs for Encoded Distributed Optimization

Dealing with the shear size and complexity of today's massive data sets requires computational platforms that can analyze data in a parallelized and distributed fashion. A major bottleneck that arises in such modern distributed computing environments is that some of the worker nodes may run slow. These nodes a.k.a.~stragglers can significantly slow down computation as the slowest node may dictate the overall computational time. A recent computational framework, called encoded optimization, creates redundancy in the data to mitigate the effect of stragglers. In this paper we develop novel mathematical understanding for this framework demonstrating its effectiveness in much broader settings than was previously understood. We also analyze the convergence behavior of iterative encoded optimization algorithms, allowing us to characterize fundamental trade-offs between convergence rate, size of data set, accuracy, computational load (or data redundancy), and straggler toleration in this framework.