What is the Value of Data? On Mathematical Methods for Data Quality Estimation
Paper and Code
Jan 09, 2020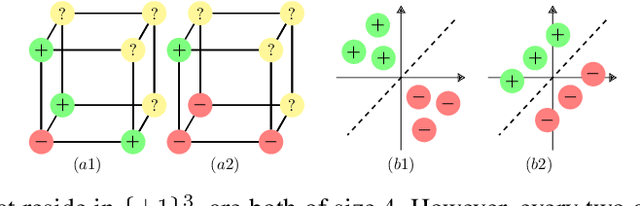
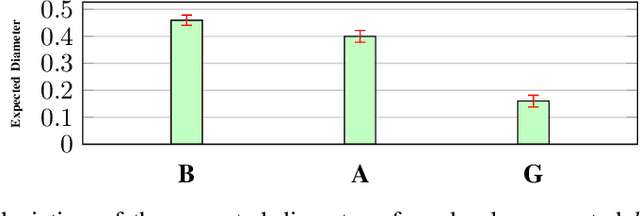
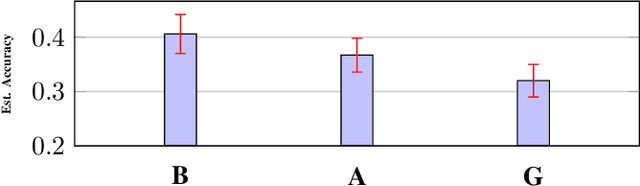
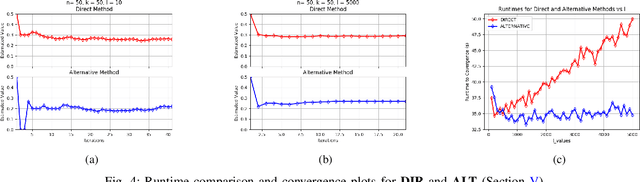
Data is one of the most important assets of the information age, and its societal impact is undisputed. Yet, rigorous methods of assessing the quality of data are lacking. In this paper, we propose a formal definition for the quality of a given dataset. We assess a dataset's quality by a quantity we call the expected diameter, which measures the expected disagreement between two randomly chosen hypotheses that explain it, and has recently found applications in active learning. We focus on Boolean hyperplanes, and utilize a collection of Fourier analytic, algebraic, and probabilistic methods to come up with theoretical guarantees and practical solutions for the computation of the expected diameter. We also study the behaviour of the expected diameter on algebraically structured datasets, conduct experiments that validate this notion of quality, and demonstrate the feasibility of our techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge