Variance-Aware Regret Bounds for Stochastic Contextual Dueling Bandits

Dueling bandits is a prominent framework for decision-making involving preferential feedback, a valuable feature that fits various applications involving human interaction, such as ranking, information retrieval, and recommendation systems. While substantial efforts have been made to minimize the cumulative regret in dueling bandits, a notable gap in the current research is the absence of regret bounds that account for the inherent uncertainty in pairwise comparisons between the dueling arms. Intuitively, greater uncertainty suggests a higher level of difficulty in the problem. To bridge this gap, this paper studies the problem of contextual dueling bandits, where the binary comparison of dueling arms is generated from a generalized linear model (GLM). We propose a new SupLinUCB-type algorithm that enjoys computational efficiency and a variance-aware regret bound $\tilde O\big(d\sqrt{\sum_{t=1}^T\sigma_t^2} + d\big)$, where $\sigma_t$ is the variance of the pairwise comparison in round $t$, $d$ is the dimension of the context vectors, and $T$ is the time horizon. Our regret bound naturally aligns with the intuitive expectation in scenarios where the comparison is deterministic, the algorithm only suffers from an $\tilde O(d)$ regret. We perform empirical experiments on synthetic data to confirm the advantage of our method over previous variance-agnostic algorithms.

Borda Regret Minimization for Generalized Linear Dueling Bandits

Dueling bandits are widely used to model preferential feedback that is prevalent in machine learning applications such as recommendation systems and ranking. In this paper, we study the Borda regret minimization problem for dueling bandits, which aims to identify the item with the highest Borda score while minimizing the cumulative regret. We propose a new and highly expressive generalized linear dueling bandits model, which covers many existing models. Surprisingly, the Borda regret minimization problem turns out to be difficult, as we prove a regret lower bound of order $\Omega(d^{2/3} T^{2/3})$, where $d$ is the dimension of contextual vectors and $T$ is the time horizon. To attain the lower bound, we propose an explore-then-commit type algorithm, which has a nearly matching regret upper bound $\tilde{O}(d^{2/3} T^{2/3})$. When the number of items/arms $K$ is small, our algorithm can achieve a smaller regret $\tilde{O}( (d \log K)^{1/3} T^{2/3})$ with proper choices of hyperparameters. We also conduct empirical experiments on both synthetic data and a simulated real-world environment, which corroborate our theoretical analysis.

Adaptive Sampling for Heterogeneous Rank Aggregation from Noisy Pairwise Comparisons

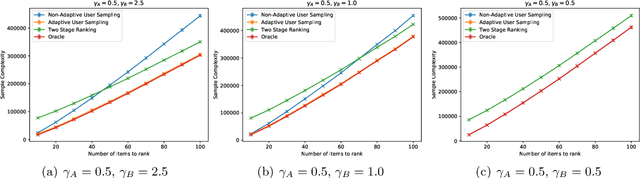
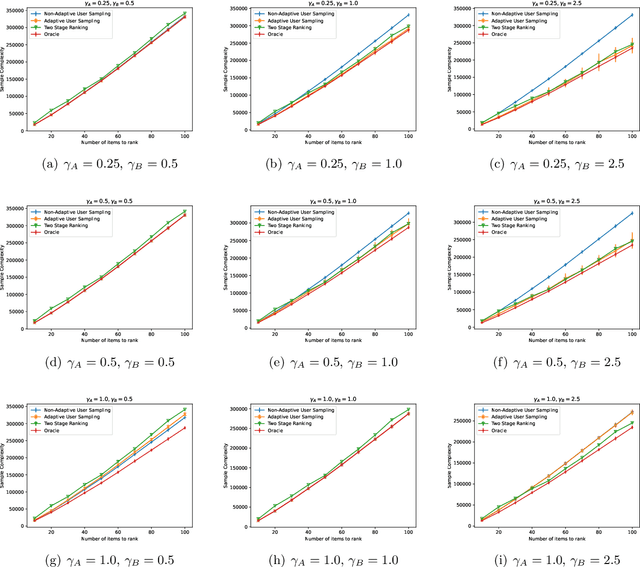
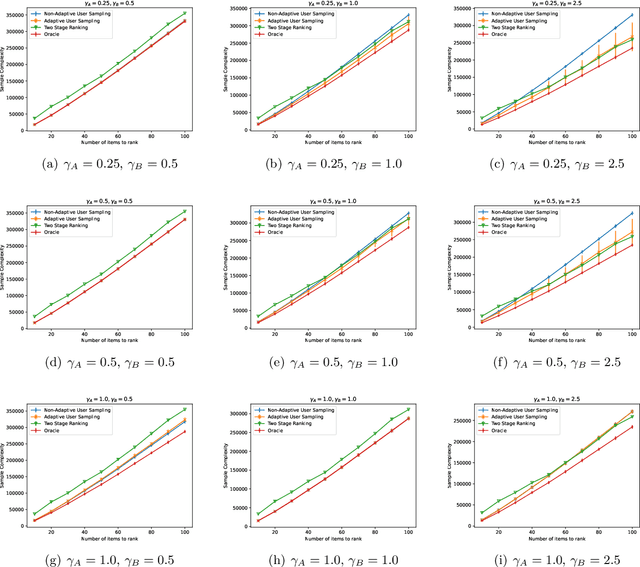
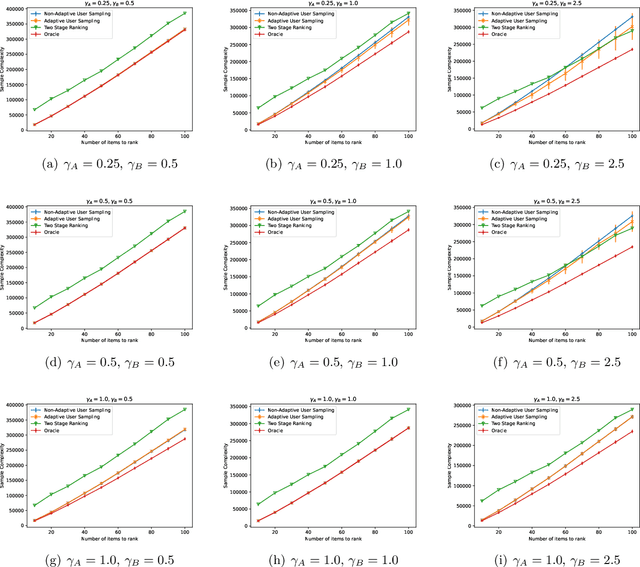
In heterogeneous rank aggregation problems, users often exhibit various accuracy levels when comparing pairs of items. Thus a uniform querying strategy over users may not be optimal. To address this issue, we propose an elimination-based active sampling strategy, which estimates the ranking of items via noisy pairwise comparisons from users and improves the users' average accuracy by maintaining an active set of users. We prove that our algorithm can return the true ranking of items with high probability. We also provide a sample complexity bound for the proposed algorithm which is better than that of non-active strategies in the literature. Experiments are provided to show the empirical advantage of the proposed methods over the state-of-the-art baselines.

Rank Aggregation via Heterogeneous Thurstone Preference Models

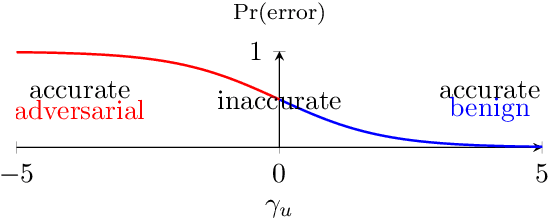
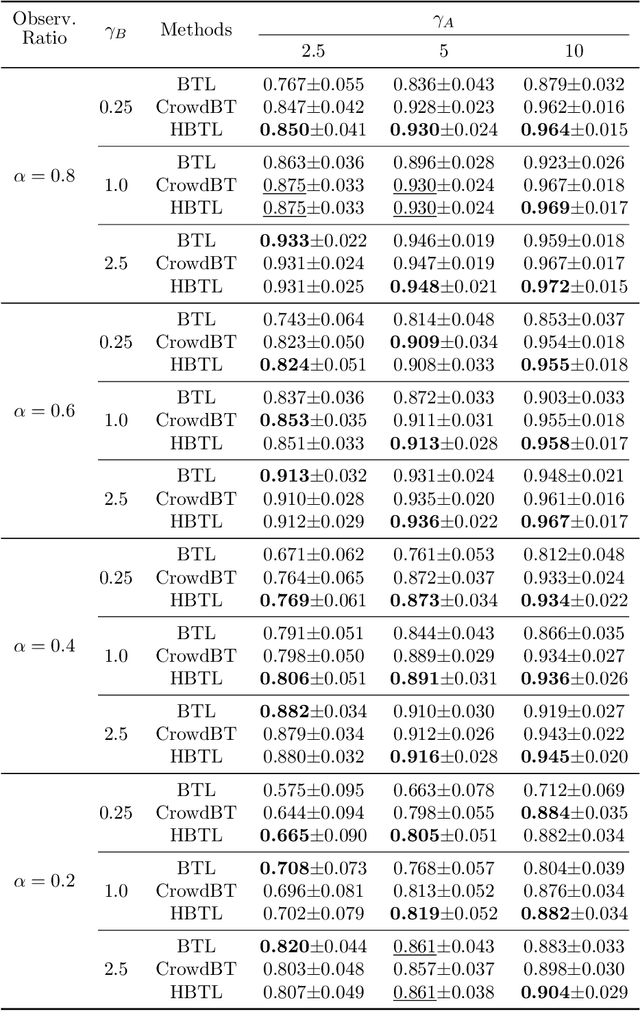
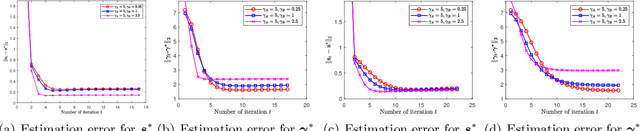
We propose the Heterogeneous Thurstone Model (HTM) for aggregating ranked data, which can take the accuracy levels of different users into account. By allowing different noise distributions, the proposed HTM model maintains the generality of Thurstone's original framework, and as such, also extends the Bradley-Terry-Luce (BTL) model for pairwise comparisons to heterogeneous populations of users. Under this framework, we also propose a rank aggregation algorithm based on alternating gradient descent to estimate the underlying item scores and accuracy levels of different users simultaneously from noisy pairwise comparisons. We theoretically prove that the proposed algorithm converges linearly up to a statistical error which matches that of the state-of-the-art method for the single-user BTL model. We evaluate the proposed HTM model and algorithm on both synthetic and real data, demonstrating that it outperforms existing methods.

The Capacity of String-Replication Systems

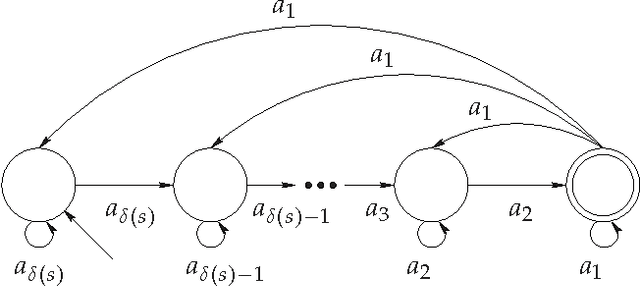
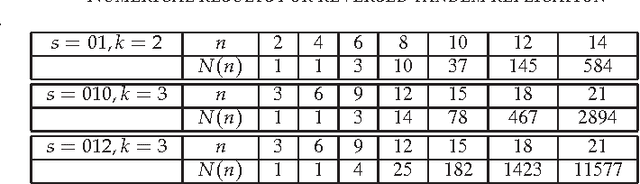
It is known that the majority of the human genome consists of repeated sequences. Furthermore, it is believed that a significant part of the rest of the genome also originated from repeated sequences and has mutated to its current form. In this paper, we investigate the possibility of constructing an exponentially large number of sequences from a short initial sequence and simple replication rules, including those resembling genomic replication processes. In other words, our goal is to find out the capacity, or the expressive power, of these string-replication systems. Our results include exact capacities, and bounds on the capacities, of four fundamental string-replication systems.