Unified Convergence Analysis for Score-Based Diffusion Models with Deterministic Samplers

Score-based diffusion models have emerged as powerful techniques for generating samples from high-dimensional data distributions. These models involve a two-phase process: first, injecting noise to transform the data distribution into a known prior distribution, and second, sampling to recover the original data distribution from noise. Among the various sampling methods, deterministic samplers stand out for their enhanced efficiency. However, analyzing these deterministic samplers presents unique challenges, as they preclude the use of established techniques such as Girsanov's theorem, which are only applicable to stochastic samplers. Furthermore, existing analysis for deterministic samplers usually focuses on specific examples, lacking a generalized approach for general forward processes and various deterministic samplers. Our paper addresses these limitations by introducing a unified convergence analysis framework. To demonstrate the power of our framework, we analyze the variance-preserving (VP) forward process with the exponential integrator (EI) scheme, achieving iteration complexity of $\tilde O(d^2/\epsilon)$. Additionally, we provide a detailed analysis of Denoising Diffusion Implicit Models (DDIM)-type samplers, which have been underexplored in previous research, achieving polynomial iteration complexity.

Relative-Translation Invariant Wasserstein Distance

We introduce a new family of distances, relative-translation invariant Wasserstein distances ($RW_p$), for measuring the similarity of two probability distributions under distribution shift. Generalizing it from the classical optimal transport model, we show that $RW_p$ distances are also real distance metrics defined on the quotient set $\mathcal{P}_p(\mathbb{R}^n)/\sim$ and invariant to distribution translations. When $p=2$, the $RW_2$ distance enjoys more exciting properties, including decomposability of the optimal transport model, translation-invariance of the $RW_2$ distance, and a Pythagorean relationship between $RW_2$ and the classical quadratic Wasserstein distance ($W_2$). Based on these properties, we show that a distribution shift, measured by $W_2$ distance, can be explained in the bias-variance perspective. In addition, we propose a variant of the Sinkhorn algorithm, named $RW_2$ Sinkhorn algorithm, for efficiently calculating $RW_2$ distance, coupling solutions, as well as $W_2$ distance. We also provide the analysis of numerical stability and time complexity for the proposed algorithm. Finally, we validate the $RW_2$ distance metric and the algorithm performance with three experiments. We conduct one numerical validation for the $RW_2$ Sinkhorn algorithm and show two real-world applications demonstrating the effectiveness of using $RW_2$ under distribution shift: digits recognition and similar thunderstorm detection. The experimental results report that our proposed algorithm significantly improves the computational efficiency of Sinkhorn in certain practical applications, and the $RW_2$ distance is robust to distribution translations compared with baselines.

Nearly Optimal Algorithms for Contextual Dueling Bandits from Adversarial Feedback

Learning from human feedback plays an important role in aligning generative models, such as large language models (LLM). However, the effectiveness of this approach can be influenced by adversaries, who may intentionally provide misleading preferences to manipulate the output in an undesirable or harmful direction. To tackle this challenge, we study a specific model within this problem domain--contextual dueling bandits with adversarial feedback, where the true preference label can be flipped by an adversary. We propose an algorithm namely robust contextual dueling bandit (\algo), which is based on uncertainty-weighted maximum likelihood estimation. Our algorithm achieves an $\tilde O(d\sqrt{T}+dC)$ regret bound, where $T$ is the number of rounds, $d$ is the dimension of the context, and $ 0 \le C \le T$ is the total number of adversarial feedback. We also prove a lower bound to show that our regret bound is nearly optimal, both in scenarios with and without ($C=0$) adversarial feedback. Additionally, we conduct experiments to evaluate our proposed algorithm against various types of adversarial feedback. Experimental results demonstrate its superiority over the state-of-the-art dueling bandit algorithms in the presence of adversarial feedback.

Nearly Minimax Optimal Regret for Learning Linear Mixture Stochastic Shortest Path

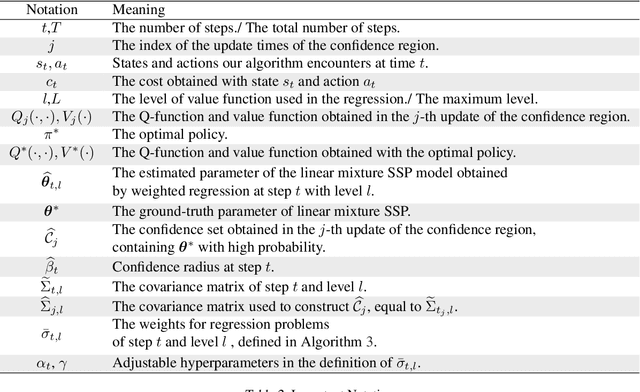
We study the Stochastic Shortest Path (SSP) problem with a linear mixture transition kernel, where an agent repeatedly interacts with a stochastic environment and seeks to reach certain goal state while minimizing the cumulative cost. Existing works often assume a strictly positive lower bound of the cost function or an upper bound of the expected length for the optimal policy. In this paper, we propose a new algorithm to eliminate these restrictive assumptions. Our algorithm is based on extended value iteration with a fine-grained variance-aware confidence set, where the variance is estimated recursively from high-order moments. Our algorithm achieves an $\tilde{\mathcal O}(dB_*\sqrt{K})$ regret bound, where $d$ is the dimension of the feature mapping in the linear transition kernel, $B_*$ is the upper bound of the total cumulative cost for the optimal policy, and $K$ is the number of episodes. Our regret upper bound matches the $\Omega(dB_*\sqrt{K})$ lower bound of linear mixture SSPs in Min et al. (2022), which suggests that our algorithm is nearly minimax optimal.

Variance-Aware Regret Bounds for Stochastic Contextual Dueling Bandits

Dueling bandits is a prominent framework for decision-making involving preferential feedback, a valuable feature that fits various applications involving human interaction, such as ranking, information retrieval, and recommendation systems. While substantial efforts have been made to minimize the cumulative regret in dueling bandits, a notable gap in the current research is the absence of regret bounds that account for the inherent uncertainty in pairwise comparisons between the dueling arms. Intuitively, greater uncertainty suggests a higher level of difficulty in the problem. To bridge this gap, this paper studies the problem of contextual dueling bandits, where the binary comparison of dueling arms is generated from a generalized linear model (GLM). We propose a new SupLinUCB-type algorithm that enjoys computational efficiency and a variance-aware regret bound $\tilde O\big(d\sqrt{\sum_{t=1}^T\sigma_t^2} + d\big)$, where $\sigma_t$ is the variance of the pairwise comparison in round $t$, $d$ is the dimension of the context vectors, and $T$ is the time horizon. Our regret bound naturally aligns with the intuitive expectation in scenarios where the comparison is deterministic, the algorithm only suffers from an $\tilde O(d)$ regret. We perform empirical experiments on synthetic data to confirm the advantage of our method over previous variance-agnostic algorithms.

Pessimistic Nonlinear Least-Squares Value Iteration for Offline Reinforcement Learning

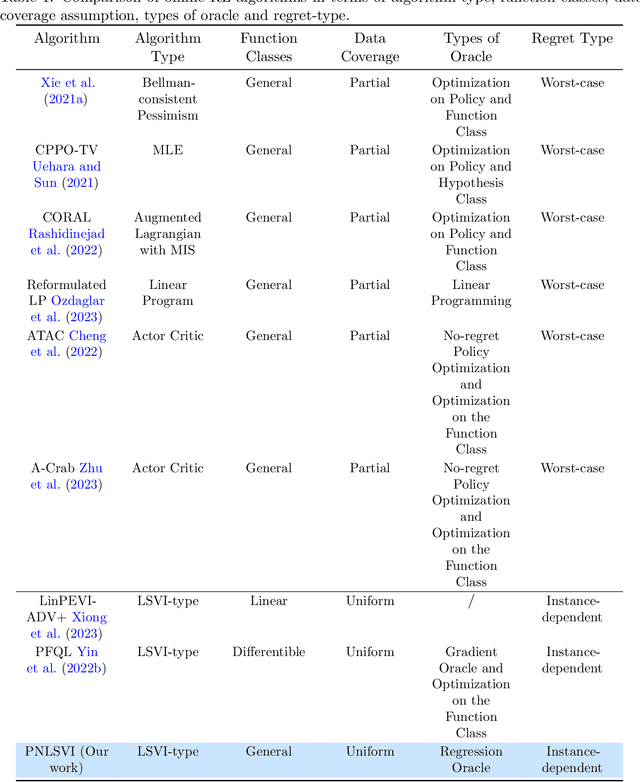
Offline reinforcement learning (RL), where the agent aims to learn the optimal policy based on the data collected by a behavior policy, has attracted increasing attention in recent years. While offline RL with linear function approximation has been extensively studied with optimal results achieved under certain assumptions, many works shift their interest to offline RL with non-linear function approximation. However, limited works on offline RL with non-linear function approximation have instance-dependent regret guarantees. In this paper, we propose an oracle-efficient algorithm, dubbed Pessimistic Nonlinear Least-Square Value Iteration (PNLSVI), for offline RL with non-linear function approximation. Our algorithmic design comprises three innovative components: (1) a variance-based weighted regression scheme that can be applied to a wide range of function classes, (2) a subroutine for variance estimation, and (3) a planning phase that utilizes a pessimistic value iteration approach. Our algorithm enjoys a regret bound that has a tight dependency on the function class complexity and achieves minimax optimal instance-dependent regret when specialized to linear function approximation. Our work extends the previous instance-dependent results within simpler function classes, such as linear and differentiable function to a more general framework.