Logarithmic Regret for Online KL-Regularized Reinforcement Learning

Recent advances in Reinforcement Learning from Human Feedback (RLHF) have shown that KL-regularization plays a pivotal role in improving the efficiency of RL fine-tuning for large language models (LLMs). Despite its empirical advantage, the theoretical difference between KL-regularized RL and standard RL remains largely under-explored. While there is a recent line of work on the theoretical analysis of KL-regularized objective in decision making \citep{xiong2024iterative, xie2024exploratory,zhao2024sharp}, these analyses either reduce to the traditional RL setting or rely on strong coverage assumptions. In this paper, we propose an optimism-based KL-regularized online contextual bandit algorithm, and provide a novel analysis of its regret. By carefully leveraging the benign optimization landscape induced by the KL-regularization and the optimistic reward estimation, our algorithm achieves an $\mathcal{O}\big(\eta\log (N_{\mathcal R} T)\cdot d_{\mathcal R}\big)$ logarithmic regret bound, where $\eta, N_{\mathcal R},T,d_{\mathcal R}$ denote the KL-regularization parameter, the cardinality of the reward function class, number of rounds, and the complexity of the reward function class. Furthermore, we extend our algorithm and analysis to reinforcement learning by developing a novel decomposition over transition steps and also obtain a similar logarithmic regret bound.

Nearly Optimal Sample Complexity of Offline KL-Regularized Contextual Bandits under Single-Policy Concentrability

KL-regularized policy optimization has become a workhorse in learning-based decision making, while its theoretical understanding is still very limited. Although recent progress has been made towards settling the sample complexity of KL-regularized contextual bandits, existing sample complexity bounds are either $\tilde{O}(\epsilon^{-2})$ under single-policy concentrability or $\tilde{O}(\epsilon^{-1})$ under all-policy concentrability. In this paper, we propose the \emph{first} algorithm with $\tilde{O}(\epsilon^{-1})$ sample complexity under single-policy concentrability for offline contextual bandits. Our algorithm is designed for general function approximation and based on the principle of \emph{pessimism in the face of uncertainty}. The core of our proof leverages the strong convexity of the KL regularization, and the conditional non-negativity of the gap between the true reward and its pessimistic estimator to refine a mean-value-type risk upper bound to its extreme. This in turn leads to a novel covariance-based analysis, effectively bypassing the need for uniform control over the discrepancy between any two functions in the function class. The near-optimality of our algorithm is demonstrated by an $\tilde{\Omega}(\epsilon^{-1})$ lower bound. Furthermore, we extend our algorithm to contextual dueling bandits and achieve a similar nearly optimal sample complexity.

Sharp Analysis for KL-Regularized Contextual Bandits and RLHF

Reverse-Kullback-Leibler (KL) regularization has emerged to be a predominant technique used to enhance policy optimization in reinforcement learning (RL) and reinforcement learning from human feedback (RLHF), which forces the learned policy to stay close to a reference policy. While the effectiveness and necessity of KL-regularization have been empirically demonstrated in various practical scenarios, current theoretical analysis of KL-regularized RLHF still obtains the same $\mathcal{O}(1 / \epsilon^2)$ sample complexity as problems without KL-regularization. To understand the fundamental distinction between policy learning objectives with KL-regularization and ones without KL-regularization, we are the first to theoretically demonstrate the power of KL-regularization by providing a sharp analysis for KL-regularized contextual bandits and RLHF, revealing an $\mathcal{O}(1 / \epsilon)$ sample complexity when $\epsilon$ is sufficiently small. We further explore the role of data coverage in contextual bandits and RLHF. While the coverage assumption is commonly employed in offline RLHF to link the samples from the reference policy to the optimal policy, often at the cost of a multiplicative dependence on the coverage coefficient, its impact on the sample complexity of online RLHF remains unclear. Previous theoretical analyses of online RLHF typically require explicit exploration and additional structural assumptions on the reward function class. In contrast, we show that with sufficient coverage from the reference policy, a simple two-stage mixed sampling strategy can achieve a sample complexity with only an additive dependence on the coverage coefficient. Our results provide a comprehensive understanding of the roles of KL-regularization and data coverage in RLHF, shedding light on the design of more efficient RLHF algorithms.

Feel-Good Thompson Sampling for Contextual Dueling Bandits

Contextual dueling bandits, where a learner compares two options based on context and receives feedback indicating which was preferred, extends classic dueling bandits by incorporating contextual information for decision-making and preference learning. Several algorithms based on the upper confidence bound (UCB) have been proposed for linear contextual dueling bandits. However, no algorithm based on posterior sampling has been developed in this setting, despite the empirical success observed in traditional contextual bandits. In this paper, we propose a Thompson sampling algorithm, named FGTS.CDB, for linear contextual dueling bandits. At the core of our algorithm is a new Feel-Good exploration term specifically tailored for dueling bandits. This term leverages the independence of the two selected arms, thereby avoiding a cross term in the analysis. We show that our algorithm achieves nearly minimax-optimal regret, i.e., $\tilde{\mathcal{O}}(d\sqrt T)$, where $d$ is the model dimension and $T$ is the time horizon. Finally, we evaluate our algorithm on synthetic data and observe that FGTS.CDB outperforms existing algorithms by a large margin.

A Nearly Optimal and Low-Switching Algorithm for Reinforcement Learning with General Function Approximation

The exploration-exploitation dilemma has been a central challenge in reinforcement learning (RL) with complex model classes. In this paper, we propose a new algorithm, Monotonic Q-Learning with Upper Confidence Bound (MQL-UCB) for RL with general function approximation. Our key algorithmic design includes (1) a general deterministic policy-switching strategy that achieves low switching cost, (2) a monotonic value function structure with carefully controlled function class complexity, and (3) a variance-weighted regression scheme that exploits historical trajectories with high data efficiency. MQL-UCB achieves minimax optimal regret of $\tilde{O}(d\sqrt{HK})$ when $K$ is sufficiently large and near-optimal policy switching cost of $\tilde{O}(dH)$, with $d$ being the eluder dimension of the function class, $H$ being the planning horizon, and $K$ being the number of episodes. Our work sheds light on designing provably sample-efficient and deployment-efficient Q-learning with nonlinear function approximation.

Variance-Aware Regret Bounds for Stochastic Contextual Dueling Bandits

Dueling bandits is a prominent framework for decision-making involving preferential feedback, a valuable feature that fits various applications involving human interaction, such as ranking, information retrieval, and recommendation systems. While substantial efforts have been made to minimize the cumulative regret in dueling bandits, a notable gap in the current research is the absence of regret bounds that account for the inherent uncertainty in pairwise comparisons between the dueling arms. Intuitively, greater uncertainty suggests a higher level of difficulty in the problem. To bridge this gap, this paper studies the problem of contextual dueling bandits, where the binary comparison of dueling arms is generated from a generalized linear model (GLM). We propose a new SupLinUCB-type algorithm that enjoys computational efficiency and a variance-aware regret bound $\tilde O\big(d\sqrt{\sum_{t=1}^T\sigma_t^2} + d\big)$, where $\sigma_t$ is the variance of the pairwise comparison in round $t$, $d$ is the dimension of the context vectors, and $T$ is the time horizon. Our regret bound naturally aligns with the intuitive expectation in scenarios where the comparison is deterministic, the algorithm only suffers from an $\tilde O(d)$ regret. We perform empirical experiments on synthetic data to confirm the advantage of our method over previous variance-agnostic algorithms.

Pessimistic Nonlinear Least-Squares Value Iteration for Offline Reinforcement Learning

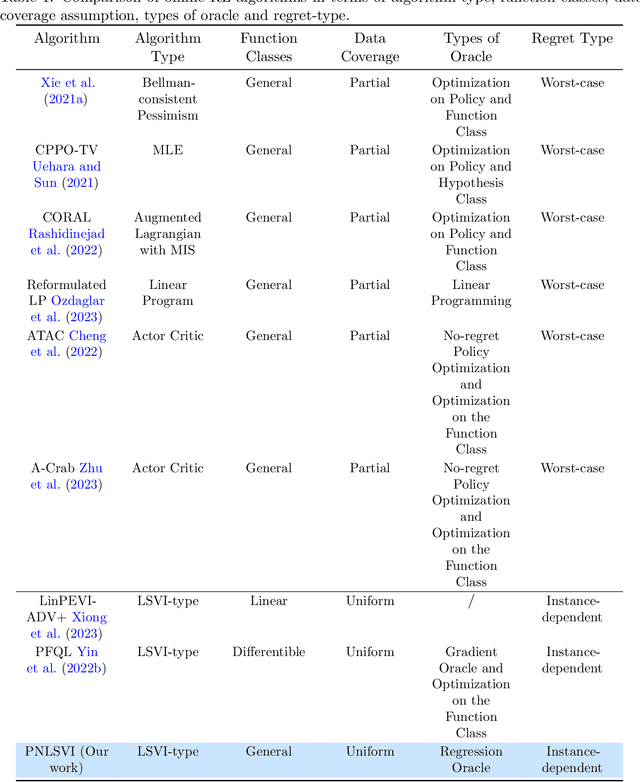
Offline reinforcement learning (RL), where the agent aims to learn the optimal policy based on the data collected by a behavior policy, has attracted increasing attention in recent years. While offline RL with linear function approximation has been extensively studied with optimal results achieved under certain assumptions, many works shift their interest to offline RL with non-linear function approximation. However, limited works on offline RL with non-linear function approximation have instance-dependent regret guarantees. In this paper, we propose an oracle-efficient algorithm, dubbed Pessimistic Nonlinear Least-Square Value Iteration (PNLSVI), for offline RL with non-linear function approximation. Our algorithmic design comprises three innovative components: (1) a variance-based weighted regression scheme that can be applied to a wide range of function classes, (2) a subroutine for variance estimation, and (3) a planning phase that utilizes a pessimistic value iteration approach. Our algorithm enjoys a regret bound that has a tight dependency on the function class complexity and achieves minimax optimal instance-dependent regret when specialized to linear function approximation. Our work extends the previous instance-dependent results within simpler function classes, such as linear and differentiable function to a more general framework.

Variance-Dependent Regret Bounds for Linear Bandits and Reinforcement Learning: Adaptivity and Computational Efficiency

Recently, several studies (Zhou et al., 2021a; Zhang et al., 2021b; Kim et al., 2021; Zhou and Gu, 2022) have provided variance-dependent regret bounds for linear contextual bandits, which interpolates the regret for the worst-case regime and the deterministic reward regime. However, these algorithms are either computationally intractable or unable to handle unknown variance of the noise. In this paper, we present a novel solution to this open problem by proposing the first computationally efficient algorithm for linear bandits with heteroscedastic noise. Our algorithm is adaptive to the unknown variance of noise and achieves an $\tilde{O}(d \sqrt{\sum_{k = 1}^K \sigma_k^2} + d)$ regret, where $\sigma_k^2$ is the variance of the noise at the round $k$, $d$ is the dimension of the contexts and $K$ is the total number of rounds. Our results are based on an adaptive variance-aware confidence set enabled by a new Freedman-type concentration inequality for self-normalized martingales and a multi-layer structure to stratify the context vectors into different layers with different uniform upper bounds on the uncertainty. Furthermore, our approach can be extended to linear mixture Markov decision processes (MDPs) in reinforcement learning. We propose a variance-adaptive algorithm for linear mixture MDPs, which achieves a problem-dependent horizon-free regret bound that can gracefully reduce to a nearly constant regret for deterministic MDPs. Unlike existing nearly minimax optimal algorithms for linear mixture MDPs, our algorithm does not require explicit variance estimation of the transitional probabilities or the use of high-order moment estimators to attain horizon-free regret. We believe the techniques developed in this paper can have independent value for general online decision making problems.

Nearly Minimax Optimal Reinforcement Learning for Linear Markov Decision Processes

We study reinforcement learning (RL) with linear function approximation. For episodic time-inhomogeneous linear Markov decision processes (linear MDPs) whose transition dynamic can be parameterized as a linear function of a given feature mapping, we propose the first computationally efficient algorithm that achieves the nearly minimax optimal regret $\tilde O(d\sqrt{H^3K})$, where $d$ is the dimension of the feature mapping, $H$ is the planning horizon, and $K$ is the number of episodes. Our algorithm is based on a weighted linear regression scheme with a carefully designed weight, which depends on a new variance estimator that (1) directly estimates the variance of the \emph{optimal} value function, (2) monotonically decreases with respect to the number of episodes to ensure a better estimation accuracy, and (3) uses a rare-switching policy to update the value function estimator to control the complexity of the estimated value function class. Our work provides a complete answer to optimal RL with linear MDPs, and the developed algorithm and theoretical tools may be of independent interest.

Bandit Learning with General Function Classes: Heteroscedastic Noise and Variance-dependent Regret Bounds

We consider learning a stochastic bandit model, where the reward function belongs to a general class of uniformly bounded functions, and the additive noise can be heteroscedastic. Our model captures contextual linear bandits and generalized linear bandits as special cases. While previous works (Kirschner and Krause, 2018; Zhou et al., 2021) based on weighted ridge regression can deal with linear bandits with heteroscedastic noise, they are not directly applicable to our general model due to the curse of nonlinearity. In order to tackle this problem, we propose a multi-level learning framework for the general bandit model. The core idea of our framework is to partition the observed data into different levels according to the variance of their respective reward and perform online learning at each level collaboratively. Under our framework, we first design an algorithm that constructs the variance-aware confidence set based on empirical risk minimization and prove a variance-dependent regret bound. For generalized linear bandits, we further propose an algorithm based on follow-the-regularized-leader (FTRL) subroutine and online-to-confidence-set conversion, which can achieve a tighter variance-dependent regret under certain conditions.