LingLanMiDian: Systematic Evaluation of LLMs on TCM Knowledge and Clinical Reasoning

Large language models (LLMs) are advancing rapidly in medical NLP, yet Traditional Chinese Medicine (TCM) with its distinctive ontology, terminology, and reasoning patterns requires domain-faithful evaluation. Existing TCM benchmarks are fragmented in coverage and scale and rely on non-unified or generation-heavy scoring that hinders fair comparison. We present the LingLanMiDian (LingLan) benchmark, a large-scale, expert-curated, multi-task suite that unifies evaluation across knowledge recall, multi-hop reasoning, information extraction, and real-world clinical decision-making. LingLan introduces a consistent metric design, a synonym-tolerant protocol for clinical labels, a per-dataset 400-item Hard subset, and a reframing of diagnosis and treatment recommendation into single-choice decision recognition. We conduct comprehensive, zero-shot evaluations on 14 leading open-source and proprietary LLMs, providing a unified perspective on their strengths and limitations in TCM commonsense knowledge understanding, reasoning, and clinical decision support; critically, the evaluation on Hard subset reveals a substantial gap between current models and human experts in TCM-specialized reasoning. By bridging fundamental knowledge and applied reasoning through standardized evaluation, LingLan establishes a unified, quantitative, and extensible foundation for advancing TCM LLMs and domain-specific medical AI research. All evaluation data and code are available at https://github.com/TCMAI-BJTU/LingLan and http://tcmnlp.com.

Extreme Event Aware ($η$-) Learning

Quantifying and predicting rare and extreme events persists as a crucial yet challenging task in understanding complex dynamical systems. Many practical challenges arise from the infrequency and severity of these events, including the considerable variance of simple sampling methods and the substantial computational cost of high-fidelity numerical simulations. Numerous data-driven methods have recently been developed to tackle these challenges. However, a typical assumption for the success of these methods is the occurrence of multiple extreme events, either within the training dataset or during the sampling process. This leads to accurate models in regions of quiescent events but with high epistemic uncertainty in regions associated with extremes. To overcome this limitation, we introduce Extreme Event Aware (e2a or eta) or $\eta$-learning which does not assume the existence of extreme events in the available data. $\eta$-learning reduces the uncertainty even in `uncharted' extreme event regions, by enforcing the extreme event statistics of an observable indicative of extremeness during training, which can be available through qualitative arguments or estimated with unlabeled data. This type of statistical regularization results in models that fit the observed data, while enforcing consistency with the prescribed observable statistics, enabling the generation of unprecedented extreme events even when the training data lack extremes therein. Theoretical results based on optimal transport offer a rigorous justification and highlight the optimality of the introduced method. Additionally, extensive numerical experiments illustrate the favorable properties of the $\eta$-learning framework on several prototype problems and real-world precipitation downscaling problems.

Theoretical Analysis for Expectation-Maximization-Based Multi-Model 3D Registration

We perform detailed theoretical analysis of an expectation-maximization-based algorithm recently proposed in for solving a variation of the 3D registration problem, named multi-model 3D registration. Despite having shown superior empirical results, did not theoretically justify the conditions under which the EM approach converges to the ground truth. In this project, we aim to close this gap by establishing such conditions. In particular, the analysis revolves around the usage of probabilistic tail bounds that are developed and applied in various instances throughout the course. The problem studied in this project stands as another example, different from those seen in the course, in which tail-bounds help advance our algorithmic understanding in a probabilistic way. We provide self-contained background materials on 3D Registration

Reducing operator complexity in Algebraic Multigrid with Machine Learning Approaches

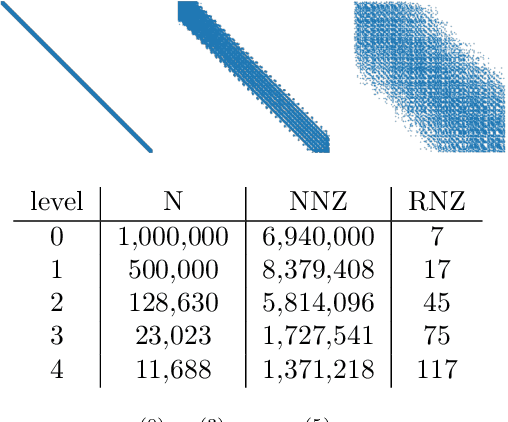
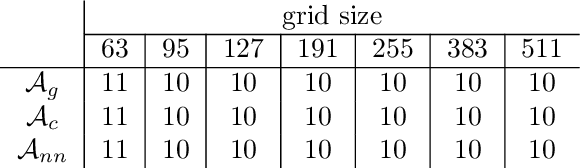
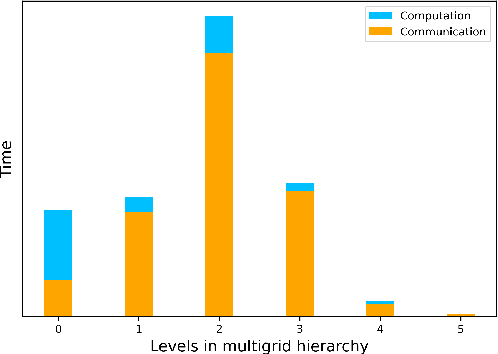
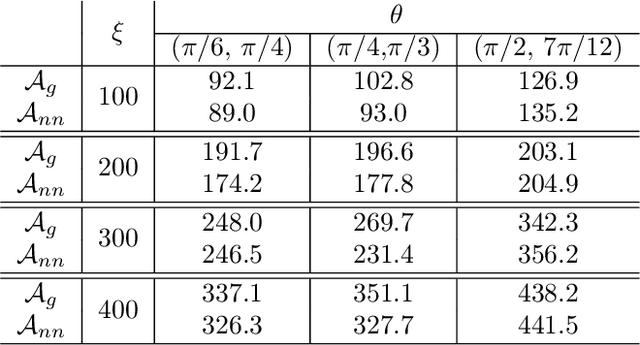
We propose a data-driven and machine-learning-based approach to compute non-Galerkin coarse-grid operators in algebraic multigrid (AMG) methods, addressing the well-known issue of increasing operator complexity. Guided by the AMG theory on spectrally equivalent coarse-grid operators, we have developed novel ML algorithms that utilize neural networks (NNs) combined with smooth test vectors from multigrid eigenvalue problems. The proposed method demonstrates promise in reducing the complexity of coarse-grid operators while maintaining overall AMG convergence for solving parametric partial differential equation (PDE) problems. Numerical experiments on anisotropic rotated Laplacian and linear elasticity problems are provided to showcase the performance and compare with existing methods for computing non-Galerkin coarse-grid operators.