Stephen Guth
Evaluation of machine learning architectures on the quantification of epistemic and aleatoric uncertainties in complex dynamical systems
Jun 27, 2023

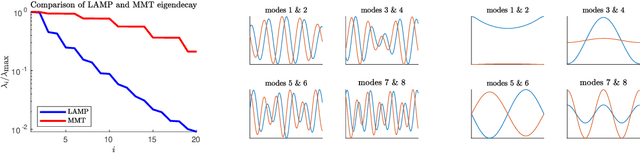
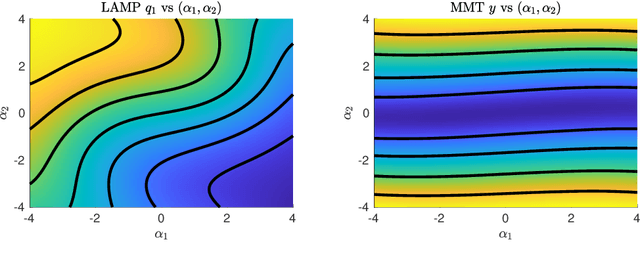
Abstract:Machine learning methods for the construction of data-driven reduced order model models are used in an increasing variety of engineering domains, especially as a supplement to expensive computational fluid dynamics for design problems. An important check on the reliability of surrogate models is Uncertainty Quantification (UQ), a self assessed estimate of the model error. Accurate UQ allows for cost savings by reducing both the required size of training data sets and the required safety factors, while poor UQ prevents users from confidently relying on model predictions. We examine several machine learning techniques, including both Gaussian processes and a family UQ-augmented neural networks: Ensemble neural networks (ENN), Bayesian neural networks (BNN), Dropout neural networks (D-NN), and Gaussian neural networks (G-NN). We evaluate UQ accuracy (distinct from model accuracy) using two metrics: the distribution of normalized residuals on validation data, and the distribution of estimated uncertainties. We apply these metrics to two model data sets, representative of complex dynamical systems: an ocean engineering problem in which a ship traverses irregular wave episodes, and a dispersive wave turbulence system with extreme events, the Majda-McLaughlin-Tabak model. We present conclusions concerning model architecture and hyperparameter tuning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge