Continuous latent representations for modeling precipitation with deep learning

The sparse and spatio-temporally discontinuous nature of precipitation data presents significant challenges for simulation and statistical processing for bias correction and downscaling. These include incorrect representation of intermittency and extreme values (critical for hydrology applications), Gibbs phenomenon upon regridding, and lack of fine scales details. To address these challenges, a common approach is to transform the precipitation variable nonlinearly into one that is more malleable. In this work, we explore how deep learning can be used to generate a smooth, spatio-temporally continuous variable as a proxy for simulation of precipitation data. We develop a normally distributed field called pseudo-precipitation (PP) as an alternative for simulating precipitation. The practical applicability of this variable is investigated by applying it for downscaling precipitation from \(1\degree\) (\(\sim\) 100 km) to \(0.25\degree\) (\(\sim\) 25 km).

TAUDiff: Improving statistical downscaling for extreme weather events using generative diffusion models

Deterministic regression-based downscaling models for climate variables often suffer from spectral bias, which can be mitigated by generative models like diffusion models. To enable efficient and reliable simulation of extreme weather events, it is crucial to achieve rapid turnaround, dynamical consistency, and accurate spatio-temporal spectral recovery. We propose an efficient correction diffusion model, TAUDiff, that combines a deterministic spatio-temporal model for mean field downscaling with a smaller generative diffusion model for recovering the fine-scale stochastic features. We demonstrate the efficacy of this approach on downscaling atmospheric wind velocity fields obtained from coarse GCM simulations. Our approach can not only ensure quicker simulation of extreme events but also reduce overall carbon footprint due to low inference times.

Modelling pressure-Hessian from local velocity gradients information in an incompressible turbulent flow field using deep neural networks

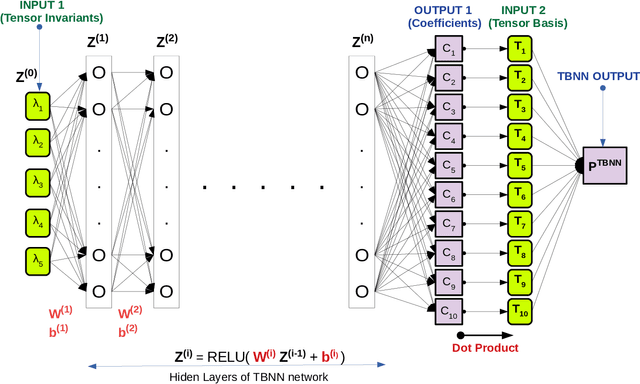
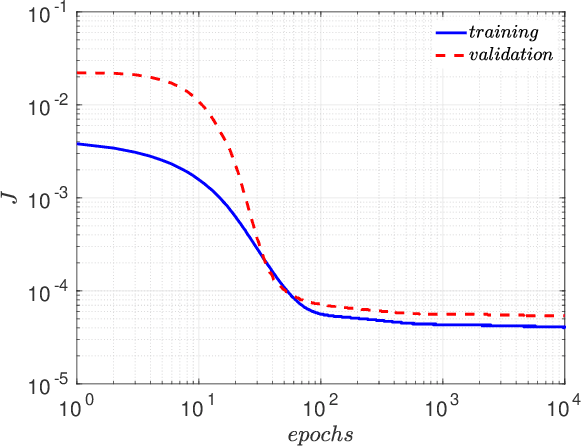
The understanding of the dynamics of the velocity gradients in turbulent flows is critical to understanding various non-linear turbulent processes. The pressure-Hessian and the viscous-Laplacian govern the evolution of the velocity-gradients and are known to be non-local in nature. Over the years, several simplified dynamical models have been proposed that models the viscous-Laplacian and the pressure-Hessian primarily in terms of local velocity gradients information. These models can also serve as closure models for the Lagrangian PDF methods. The recent fluid deformation closure model (RFDM) has been shown to retrieve excellent one-time statistics of the viscous process. However, the pressure-Hessian modelled by the RFDM has various physical limitations. In this work, we first demonstrate the limitations of the RFDM in estimating the pressure-Hessian. Further, we employ a tensor basis neural network (TBNN) to model the pressure-Hessian from the velocity gradient tensor itself. The neural network is trained on high-resolution data obtained from direct numerical simulation (DNS) of isotropic turbulence at Reynolds number of 433 (JHU turbulence database, JHTD). The predictions made by the TBNN are tested against two different isotropic turbulence datasets at Reynolds number of 433 (JHTD) and 315 (UP Madrid turbulence database, UPMTD) and channel flow dataset at Reynolds number of 1000 (UT Texas and JHTD). The evaluation of the neural network output is made in terms of the alignment statistics of the predicted pressure-Hessian eigenvectors with the strain-rate eigenvectors for turbulent isotropic flow as well as channel flow. Our analysis of the predicted solution leads to the discovery of ten unique coefficients of the tensor basis of strain-rate and rotation-rate tensors, the linear combination over which accurately captures key alignment statistics of the pressure-Hessian tensor.

Distributed physics informed neural network for data-efficient solution to partial differential equations

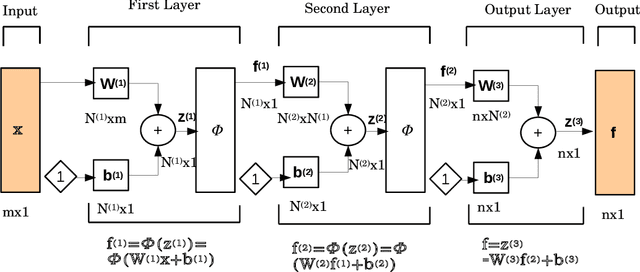
The physics informed neural network (PINN) is evolving as a viable method to solve partial differential equations. In the recent past PINNs have been successfully tested and validated to find solutions to both linear and non-linear partial differential equations (PDEs). However, the literature lacks detailed investigation of PINNs in terms of their representation capability. In this work, we first test the original PINN method in terms of its capability to represent a complicated function. Further, to address the shortcomings of the PINN architecture, we propose a novel distributed PINN, named DPINN. We first perform a direct comparison of the proposed DPINN approach against PINN to solve a non-linear PDE (Burgers' equation). We show that DPINN not only yields a more accurate solution to the Burgers' equation, but it is found to be more data-efficient as well. At last, we employ our novel DPINN to two-dimensional steady-state Navier-Stokes equation, which is a system of non-linear PDEs. To the best of the authors' knowledge, this is the first such attempt to directly solve the Navier-Stokes equation using a physics informed neural network.