PICS in Pics: Physics Informed Contour Selection for Rapid Image Segmentation

Effective training of deep image segmentation models is challenging due to the need for abundant, high-quality annotations. Generating annotations is laborious and time-consuming for human experts, especially in medical image segmentation. To facilitate image annotation, we introduce Physics Informed Contour Selection (PICS) - an interpretable, physics-informed algorithm for rapid image segmentation without relying on labeled data. PICS draws inspiration from physics-informed neural networks (PINNs) and an active contour model called snake. It is fast and computationally lightweight because it employs cubic splines instead of a deep neural network as a basis function. Its training parameters are physically interpretable because they directly represent control knots of the segmentation curve. Traditional snakes involve minimization of the edge-based loss functionals by deriving the Euler-Lagrange equation followed by its numerical solution. However, PICS directly minimizes the loss functional, bypassing the Euler Lagrange equations. It is the first snake variant to minimize a region-based loss function instead of traditional edge-based loss functions. PICS uniquely models the three-dimensional (3D) segmentation process with an unsteady partial differential equation (PDE), which allows accelerated segmentation via transfer learning. To demonstrate its effectiveness, we apply PICS for 3D segmentation of the left ventricle on a publicly available cardiac dataset. While doing so, we also introduce a new convexity-preserving loss term that encodes the shape information of the left ventricle to enhance PICS's segmentation quality. Overall, PICS presents several novelties in network architecture, transfer learning, and physics-inspired losses for image segmentation, thereby showing promising outcomes and potential for further refinement.

Numerical Approximation in CFD Problems Using Physics Informed Machine Learning

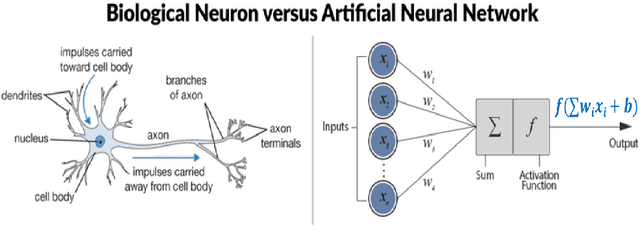
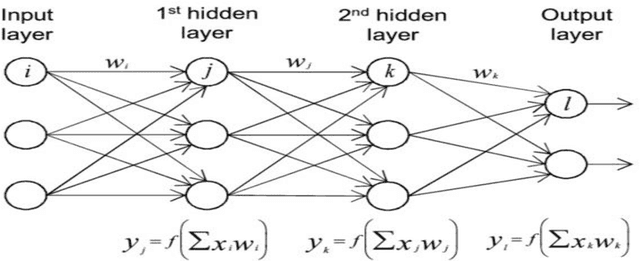
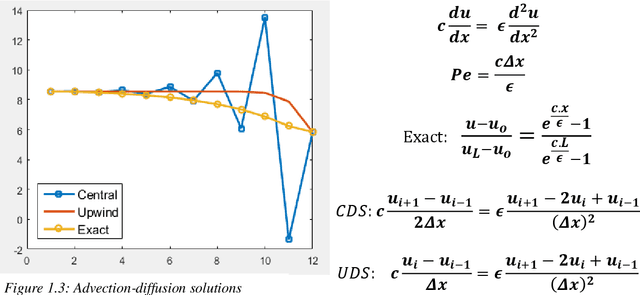
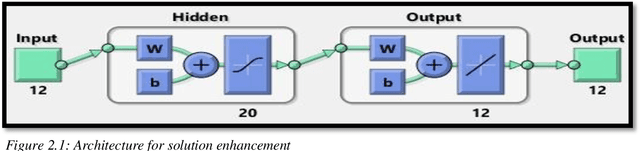
The thesis focuses on various techniques to find an alternate approximation method that could be universally used for a wide range of CFD problems but with low computational cost and low runtime. Various techniques have been explored within the field of machine learning to gauge the utility in fulfilling the core ambition. Steady advection diffusion problem has been used as the test case to understand the level of complexity up to which a method can provide solution. Ultimately, the focus stays over physics informed machine learning techniques where solving differential equations is possible without any training with computed data. The prevalent methods by I.E. Lagaris et.al. and M. Raissi et.al are explored thoroughly. The prevalent methods cannot solve advection dominant problems. A physics informed method, called as Distributed Physics Informed Neural Network (DPINN), is proposed to solve advection dominant problems. It increases the lexibility and capability of older methods by splitting the domain and introducing other physics-based constraints as mean squared loss terms. Various experiments are done to explore the end to end possibilities with the method. Parametric study is also done to understand the behavior of the method to different tunable parameters. The method is tested over steady advection-diffusion problems and unsteady square pulse problems. Very accurate results are recorded. Extreme learning machine (ELM) is a very fast neural network algorithm at the cost of tunable parameters. The ELM based variant of the proposed model is tested over the advection-diffusion problem. ELM makes the complex optimization simpler and Since the method is non-iterative, the solution is recorded in a single shot. The ELM based variant seems to work better than the simple DPINN method. Simultaneously scope for various development in future are hinted throughout the thesis.

Abstracting Deep Neural Networks into Concept Graphs for Concept Level Interpretability

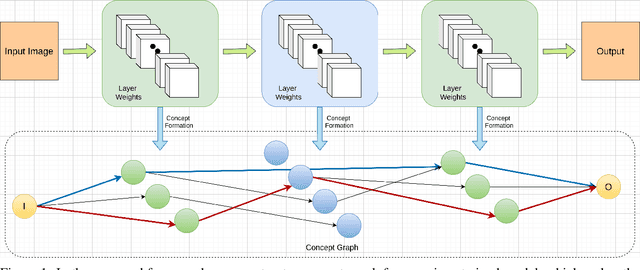
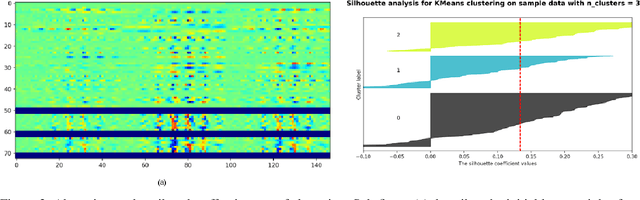
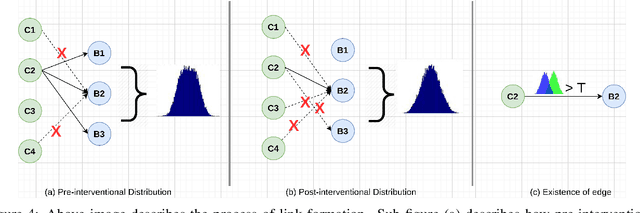
The black-box nature of deep learning models prevents them from being completely trusted in domains like biomedicine. Most explainability techniques do not capture the concept-based reasoning that human beings follow. In this work, we attempt to understand the behavior of trained models that perform image processing tasks in the medical domain by building a graphical representation of the concepts they learn. Extracting such a graphical representation of the model's behavior on an abstract, higher conceptual level would unravel the learnings of these models and would help us to evaluate the steps taken by the model for predictions. We show the application of our proposed implementation on two biomedical problems - brain tumor segmentation and fundus image classification. We provide an alternative graphical representation of the model by formulating a \textit{concept level graph} as discussed above, which makes the problem of intervention to find active inference trails more tractable. Understanding these trails would provide an understanding of the hierarchy of the decision-making process followed by the model. [As well as overall nature of model]. Our framework is available at \url{https://github.com/koriavinash1/BioExp}

A Generalized Deep Learning Framework for Whole-Slide Image Segmentation and Analysis

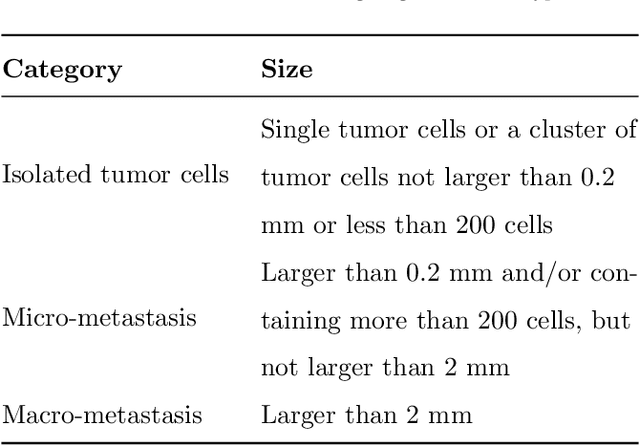
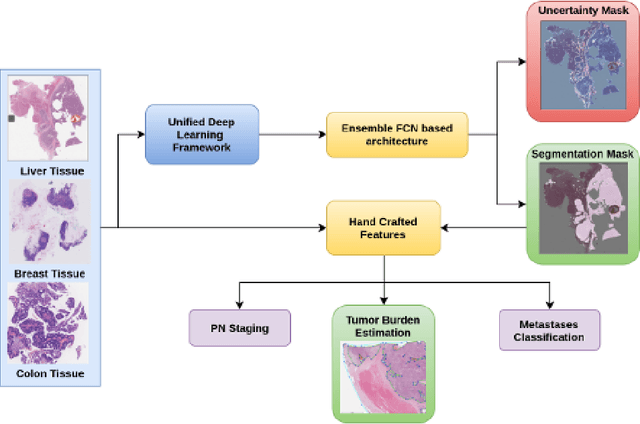
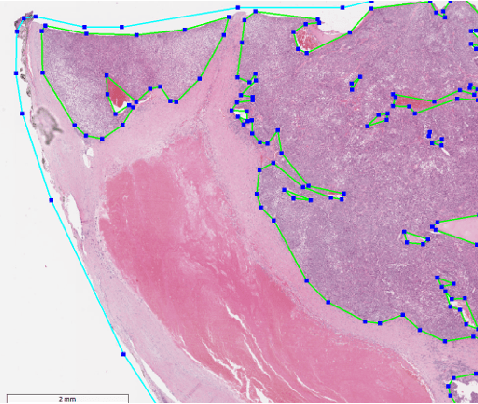
Histopathology tissue analysis is considered the gold standard in cancer diagnosis and prognosis. Given the large size of these images and the increase in the number of potential cancer cases, an automated solution as an aid to histopathologists is highly desirable. In the recent past, deep learning-based techniques have provided state of the art results in a wide variety of image analysis tasks, including analysis of digitized slides. However, the size of images and variability in histopathology tasks makes it a challenge to develop an integrated framework for histopathology image analysis. We propose a deep learning-based framework for histopathology tissue analysis. We demonstrate the generalizability of our framework, including training and inference, on several open-source datasets, which include CAMELYON (breast cancer metastases), DigestPath (colon cancer), and PAIP (liver cancer) datasets. We discuss multiple types of uncertainties pertaining to data and model, namely aleatoric and epistemic, respectively. Simultaneously, we demonstrate our model generalization across different data distribution by evaluating some samples on TCGA data. On CAMELYON16 test data (n=139) for the task of lesion detection, the FROC score achieved was 0.86 and in the CAMELYON17 test-data (n=500) for the task of pN-staging the Cohen's kappa score achieved was 0.9090 (third in the open leaderboard). On DigestPath test data (n=212) for the task of tumor segmentation, a Dice score of 0.782 was achieved (fourth in the challenge). On PAIP test data (n=40) for the task of viable tumor segmentation, a Jaccard Index of 0.75 (third in the challenge) was achieved, and for viable tumor burden, a score of 0.633 was achieved (second in the challenge). Our entire framework and related documentation are freely available at GitHub and PyPi.

Modelling pressure-Hessian from local velocity gradients information in an incompressible turbulent flow field using deep neural networks

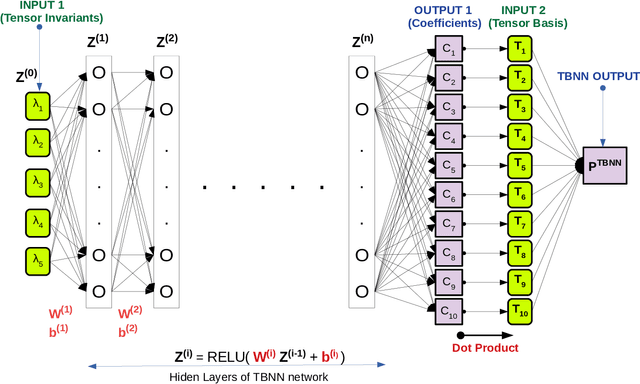
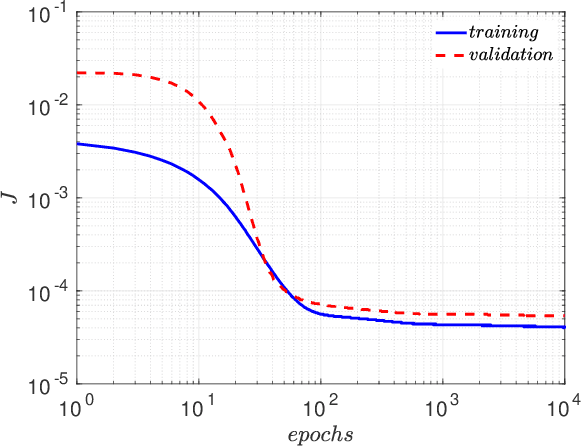
The understanding of the dynamics of the velocity gradients in turbulent flows is critical to understanding various non-linear turbulent processes. The pressure-Hessian and the viscous-Laplacian govern the evolution of the velocity-gradients and are known to be non-local in nature. Over the years, several simplified dynamical models have been proposed that models the viscous-Laplacian and the pressure-Hessian primarily in terms of local velocity gradients information. These models can also serve as closure models for the Lagrangian PDF methods. The recent fluid deformation closure model (RFDM) has been shown to retrieve excellent one-time statistics of the viscous process. However, the pressure-Hessian modelled by the RFDM has various physical limitations. In this work, we first demonstrate the limitations of the RFDM in estimating the pressure-Hessian. Further, we employ a tensor basis neural network (TBNN) to model the pressure-Hessian from the velocity gradient tensor itself. The neural network is trained on high-resolution data obtained from direct numerical simulation (DNS) of isotropic turbulence at Reynolds number of 433 (JHU turbulence database, JHTD). The predictions made by the TBNN are tested against two different isotropic turbulence datasets at Reynolds number of 433 (JHTD) and 315 (UP Madrid turbulence database, UPMTD) and channel flow dataset at Reynolds number of 1000 (UT Texas and JHTD). The evaluation of the neural network output is made in terms of the alignment statistics of the predicted pressure-Hessian eigenvectors with the strain-rate eigenvectors for turbulent isotropic flow as well as channel flow. Our analysis of the predicted solution leads to the discovery of ten unique coefficients of the tensor basis of strain-rate and rotation-rate tensors, the linear combination over which accurately captures key alignment statistics of the pressure-Hessian tensor.

Distributed physics informed neural network for data-efficient solution to partial differential equations

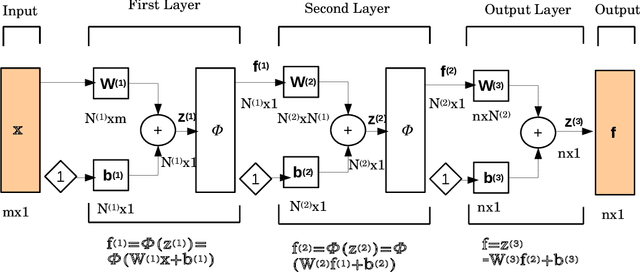
The physics informed neural network (PINN) is evolving as a viable method to solve partial differential equations. In the recent past PINNs have been successfully tested and validated to find solutions to both linear and non-linear partial differential equations (PDEs). However, the literature lacks detailed investigation of PINNs in terms of their representation capability. In this work, we first test the original PINN method in terms of its capability to represent a complicated function. Further, to address the shortcomings of the PINN architecture, we propose a novel distributed PINN, named DPINN. We first perform a direct comparison of the proposed DPINN approach against PINN to solve a non-linear PDE (Burgers' equation). We show that DPINN not only yields a more accurate solution to the Burgers' equation, but it is found to be more data-efficient as well. At last, we employ our novel DPINN to two-dimensional steady-state Navier-Stokes equation, which is a system of non-linear PDEs. To the best of the authors' knowledge, this is the first such attempt to directly solve the Navier-Stokes equation using a physics informed neural network.

Physics Informed Extreme Learning Machine (PIELM) -- A rapid method for the numerical solution of partial differential equations

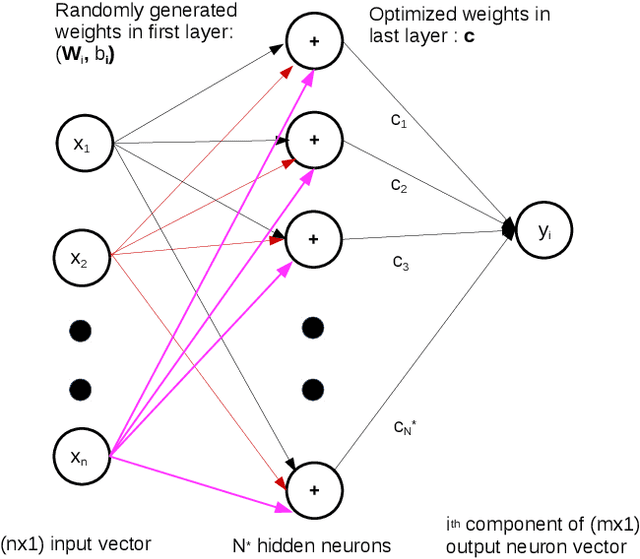
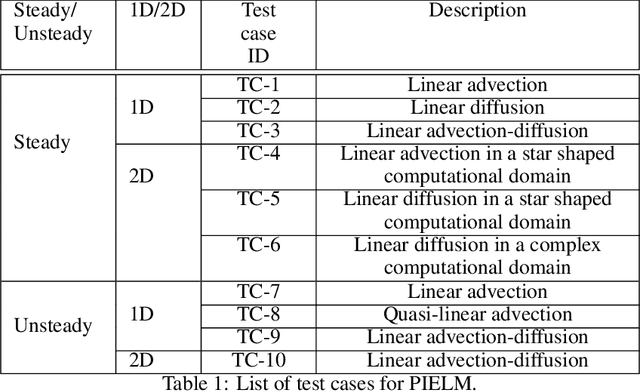
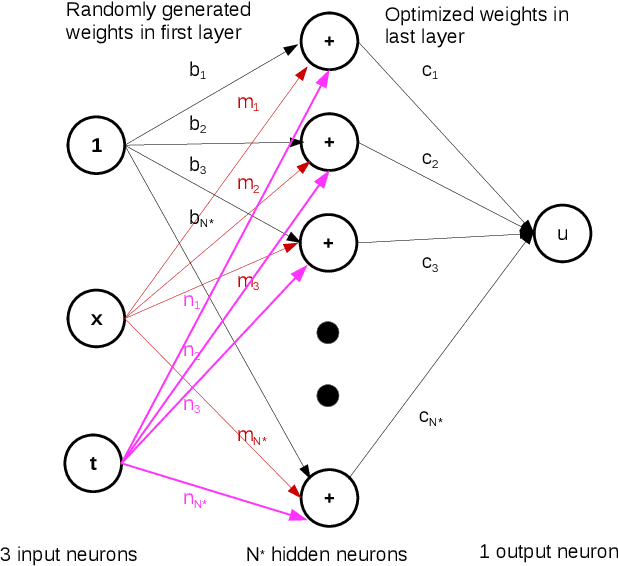
There has been rapid progress recently on the application of deep networks to the solution of partial differential equations, collectively labelled as Physics Informed Neural Networks (PINNs). In this paper, we develop Physics Informed Extreme Learning Machine (PIELM), a rapid version of PINNs which can be applied to stationary and time dependent linear partial differential equations. We demonstrate that PIELM matches or exceeds the accuracy of PINNs on a range of problems. We also discuss the limitations of neural network based approaches, including our PIELM, in the solution of PDEs on large domains and suggest an extension, a distributed version of our algorithm -{}- DPIELM. We show that DPIELM produces excellent results comparable to conventional numerical techniques in the solution of time-dependent problems. Collectively, this work contributes towards making the use of neural networks in the solution of partial differential equations in complex domains as a competitive alternative to conventional discretization techniques.

Enhanced Image Classification With Data Augmentation Using Position Coordinates

In this paper we propose the use of image pixel position coordinate system to improve image classification accuracy in various applications. Specifically, we hypothesize that the use of pixel coordinates will lead to (a) Resolution invariant performance. Here, by resolution we mean the spacing between the pixels rather than the size of the image matrix. (b) Overall improvement in classification accuracy in comparison with network models trained without local pixel coordinates. This is due to position coordinates enabling the network to learn relationship between parts of objects, mimicking the human vision system. We demonstrate our hypothesis using empirical results and intuitive explanations of the feature maps learnt by deep neural networks. Specifically, our approach showed improvements in MNIST digit classification and beats state of the results on the SVHN database. We also show that the performance of our networks is unaffected despite training the same using blurred images of the MNIST database and predicting on the high resolution database.