Global versus Local: Evaluating AlexNet Architectures for Tropical Cyclone Intensity Estimation

Given the destructive impacts of tropical cyclones, it is critical to have a reliable system for cyclone intensity detection. Various techniques are available for this purpose, each with differing levels of accuracy. In this paper, we introduce two ensemble-based models based on AlexNet architecture to estimate tropical cyclone intensity using visible satellite images. The first model, trained on the entire dataset, is called the global AlexNet model. The second model is a distributed version of AlexNet in which multiple AlexNets are trained separately on subsets of the training data categorized according to the Saffir-Simpson wind speed scale prescribed by the meterologists. We evaluated the performance of both models against a deep learning benchmark model called \textit{Deepti} using a publicly available cyclone image dataset. Results indicate that both the global model (with a root mean square error (RMSE) of 9.03 knots) and the distributed model (with a RMSE of 9.3 knots) outperform the benchmark model (with a RMSE of 13.62 knots). We provide a thorough discussion of our solution approach, including an explanantion of the AlexNet's performance using gradient class activation maps (grad-CAM). Our proposed solution strategy allows future experimentation with various deep learning models in both single and multi-channel settings.

PICS in Pics: Physics Informed Contour Selection for Rapid Image Segmentation

Effective training of deep image segmentation models is challenging due to the need for abundant, high-quality annotations. Generating annotations is laborious and time-consuming for human experts, especially in medical image segmentation. To facilitate image annotation, we introduce Physics Informed Contour Selection (PICS) - an interpretable, physics-informed algorithm for rapid image segmentation without relying on labeled data. PICS draws inspiration from physics-informed neural networks (PINNs) and an active contour model called snake. It is fast and computationally lightweight because it employs cubic splines instead of a deep neural network as a basis function. Its training parameters are physically interpretable because they directly represent control knots of the segmentation curve. Traditional snakes involve minimization of the edge-based loss functionals by deriving the Euler-Lagrange equation followed by its numerical solution. However, PICS directly minimizes the loss functional, bypassing the Euler Lagrange equations. It is the first snake variant to minimize a region-based loss function instead of traditional edge-based loss functions. PICS uniquely models the three-dimensional (3D) segmentation process with an unsteady partial differential equation (PDE), which allows accelerated segmentation via transfer learning. To demonstrate its effectiveness, we apply PICS for 3D segmentation of the left ventricle on a publicly available cardiac dataset. While doing so, we also introduce a new convexity-preserving loss term that encodes the shape information of the left ventricle to enhance PICS's segmentation quality. Overall, PICS presents several novelties in network architecture, transfer learning, and physics-inspired losses for image segmentation, thereby showing promising outcomes and potential for further refinement.

Numerical Approximation in CFD Problems Using Physics Informed Machine Learning

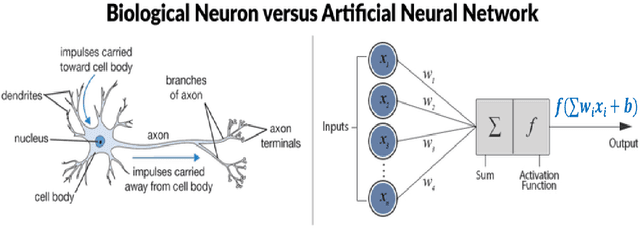
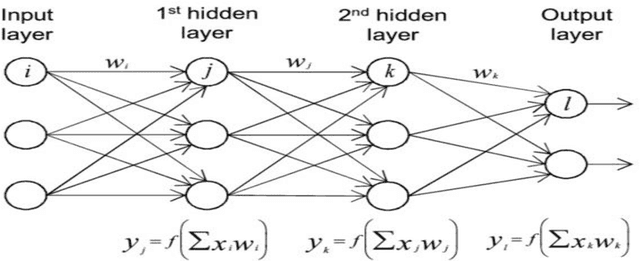
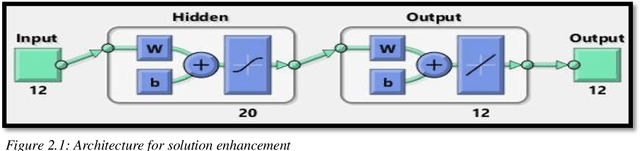
The thesis focuses on various techniques to find an alternate approximation method that could be universally used for a wide range of CFD problems but with low computational cost and low runtime. Various techniques have been explored within the field of machine learning to gauge the utility in fulfilling the core ambition. Steady advection diffusion problem has been used as the test case to understand the level of complexity up to which a method can provide solution. Ultimately, the focus stays over physics informed machine learning techniques where solving differential equations is possible without any training with computed data. The prevalent methods by I.E. Lagaris et.al. and M. Raissi et.al are explored thoroughly. The prevalent methods cannot solve advection dominant problems. A physics informed method, called as Distributed Physics Informed Neural Network (DPINN), is proposed to solve advection dominant problems. It increases the lexibility and capability of older methods by splitting the domain and introducing other physics-based constraints as mean squared loss terms. Various experiments are done to explore the end to end possibilities with the method. Parametric study is also done to understand the behavior of the method to different tunable parameters. The method is tested over steady advection-diffusion problems and unsteady square pulse problems. Very accurate results are recorded. Extreme learning machine (ELM) is a very fast neural network algorithm at the cost of tunable parameters. The ELM based variant of the proposed model is tested over the advection-diffusion problem. ELM makes the complex optimization simpler and Since the method is non-iterative, the solution is recorded in a single shot. The ELM based variant seems to work better than the simple DPINN method. Simultaneously scope for various development in future are hinted throughout the thesis.

Distributed physics informed neural network for data-efficient solution to partial differential equations

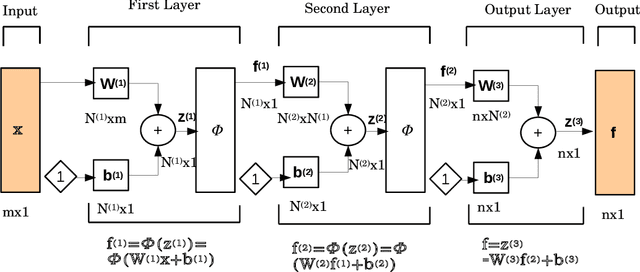
The physics informed neural network (PINN) is evolving as a viable method to solve partial differential equations. In the recent past PINNs have been successfully tested and validated to find solutions to both linear and non-linear partial differential equations (PDEs). However, the literature lacks detailed investigation of PINNs in terms of their representation capability. In this work, we first test the original PINN method in terms of its capability to represent a complicated function. Further, to address the shortcomings of the PINN architecture, we propose a novel distributed PINN, named DPINN. We first perform a direct comparison of the proposed DPINN approach against PINN to solve a non-linear PDE (Burgers' equation). We show that DPINN not only yields a more accurate solution to the Burgers' equation, but it is found to be more data-efficient as well. At last, we employ our novel DPINN to two-dimensional steady-state Navier-Stokes equation, which is a system of non-linear PDEs. To the best of the authors' knowledge, this is the first such attempt to directly solve the Navier-Stokes equation using a physics informed neural network.

Physics Informed Extreme Learning Machine (PIELM) -- A rapid method for the numerical solution of partial differential equations

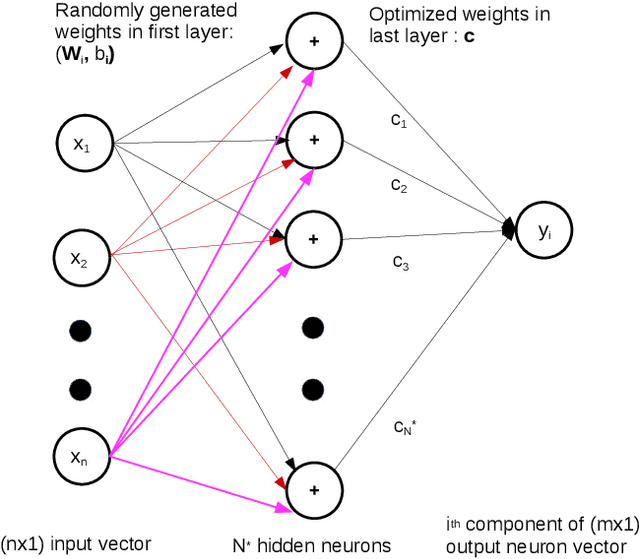
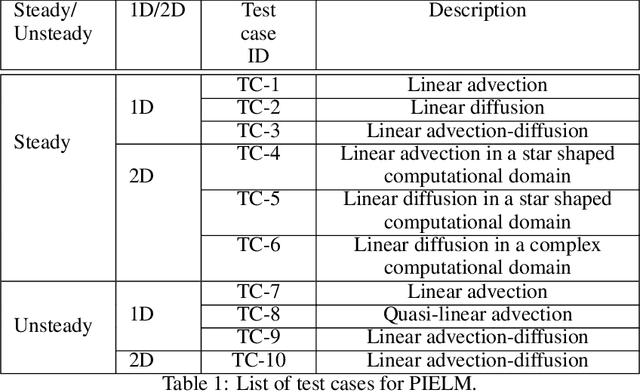
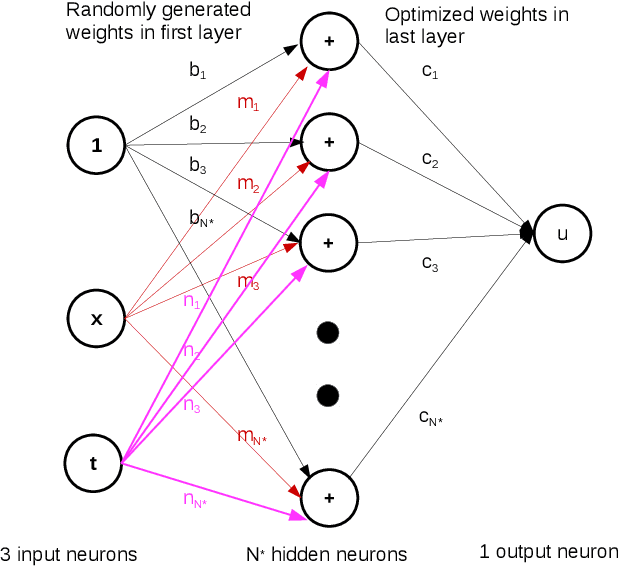
There has been rapid progress recently on the application of deep networks to the solution of partial differential equations, collectively labelled as Physics Informed Neural Networks (PINNs). In this paper, we develop Physics Informed Extreme Learning Machine (PIELM), a rapid version of PINNs which can be applied to stationary and time dependent linear partial differential equations. We demonstrate that PIELM matches or exceeds the accuracy of PINNs on a range of problems. We also discuss the limitations of neural network based approaches, including our PIELM, in the solution of PDEs on large domains and suggest an extension, a distributed version of our algorithm -{}- DPIELM. We show that DPIELM produces excellent results comparable to conventional numerical techniques in the solution of time-dependent problems. Collectively, this work contributes towards making the use of neural networks in the solution of partial differential equations in complex domains as a competitive alternative to conventional discretization techniques.