Distributed physics informed neural network for data-efficient solution to partial differential equations
Paper and Code
Jul 21, 2019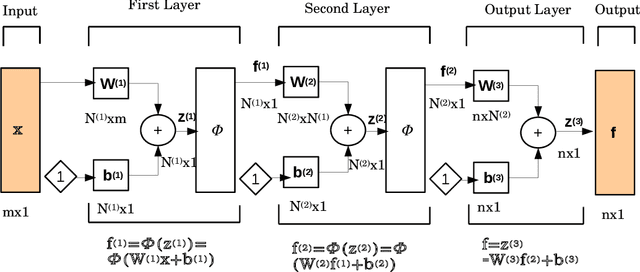



The physics informed neural network (PINN) is evolving as a viable method to solve partial differential equations. In the recent past PINNs have been successfully tested and validated to find solutions to both linear and non-linear partial differential equations (PDEs). However, the literature lacks detailed investigation of PINNs in terms of their representation capability. In this work, we first test the original PINN method in terms of its capability to represent a complicated function. Further, to address the shortcomings of the PINN architecture, we propose a novel distributed PINN, named DPINN. We first perform a direct comparison of the proposed DPINN approach against PINN to solve a non-linear PDE (Burgers' equation). We show that DPINN not only yields a more accurate solution to the Burgers' equation, but it is found to be more data-efficient as well. At last, we employ our novel DPINN to two-dimensional steady-state Navier-Stokes equation, which is a system of non-linear PDEs. To the best of the authors' knowledge, this is the first such attempt to directly solve the Navier-Stokes equation using a physics informed neural network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge