Nikolaus A. Adams
Technical University of Munich
Method of data forward generation with partial differential equations for machine learning modeling in fluid mechanics
Jan 06, 2025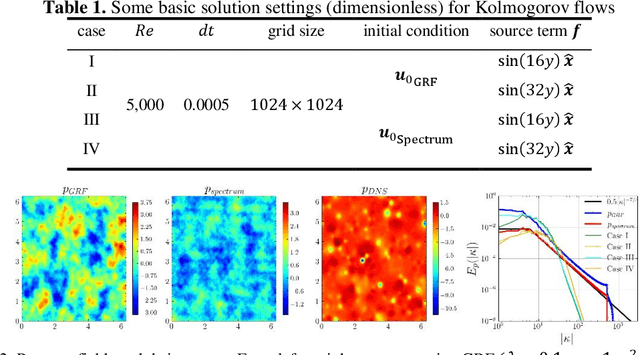



Abstract:Artificial intelligence (AI) for fluid mechanics has become attractive topic. High-fidelity data is one of most critical issues for the successful applications of AI in fluid mechanics, however, it is expensively obtained or even inaccessible. This study proposes a high-efficient data forward generation method from the partial differential equations (PDEs). Specifically, the solutions of the PDEs are first generated either following a random field (e.g. Gaussian random field, GRF, computational complexity O(NlogN), N is the number of spatial points) or physical laws (e.g. a kind of spectra, computational complexity O(NM), M is the number of modes), then the source terms, boundary conditions and initial conditions are computed to satisfy PDEs. Thus, the data pairs of source terms, boundary conditions and initial conditions with corresponding solutions of PDEs can be constructed. A Poisson neural network (Poisson-NN) embedded in projection method and a wavelet transform convolutional neuro network (WTCNN) embedded in multigrid numerical simulation for solving incompressible Navier-Stokes equations is respectively proposed. The feasibility of generated data for training Poisson-NN and WTCNN is validated. The results indicate that even without any DNS data, the generated data can train these two models with excellent generalization and accuracy. The data following physical laws can significantly improve the convergence rate, generalization and accuracy than that generated following GRF.
Rational-WENO: A lightweight, physically-consistent three-point weighted essentially non-oscillatory scheme
Sep 13, 2024



Abstract:Conventional WENO3 methods are known to be highly dissipative at lower resolutions, introducing significant errors in the pre-asymptotic regime. In this paper, we employ a rational neural network to accurately estimate the local smoothness of the solution, dynamically adapting the stencil weights based on local solution features. As rational neural networks can represent fast transitions between smooth and sharp regimes, this approach achieves a granular reconstruction with significantly reduced dissipation, improving the accuracy of the simulation. The network is trained offline on a carefully chosen dataset of analytical functions, bypassing the need for differentiable solvers. We also propose a robust model selection criterion based on estimates of the interpolation's convergence order on a set of test functions, which correlates better with the model performance in downstream tasks. We demonstrate the effectiveness of our approach on several one-, two-, and three-dimensional fluid flow problems: our scheme generalizes across grid resolutions while handling smooth and discontinuous solutions. In most cases, our rational network-based scheme achieves higher accuracy than conventional WENO3 with the same stencil size, and in a few of them, it achieves accuracy comparable to WENO5, which uses a larger stencil.
JAX-SPH: A Differentiable Smoothed Particle Hydrodynamics Framework
Mar 07, 2024



Abstract:Particle-based fluid simulations have emerged as a powerful tool for solving the Navier-Stokes equations, especially in cases that include intricate physics and free surfaces. The recent addition of machine learning methods to the toolbox for solving such problems is pushing the boundary of the quality vs. speed tradeoff of such numerical simulations. In this work, we lead the way to Lagrangian fluid simulators compatible with deep learning frameworks, and propose JAX-SPH - a Smoothed Particle Hydrodynamics (SPH) framework implemented in JAX. JAX-SPH builds on the code for dataset generation from the LagrangeBench project (Toshev et al., 2023) and extends this code in multiple ways: (a) integration of further key SPH algorithms, (b) restructuring the code toward a Python library, (c) verification of the gradients through the solver, and (d) demonstration of the utility of the gradients for solving inverse problems as well as a Solver-in-the-Loop application. Our code is available at https://github.com/tumaer/jax-sph.
Neural SPH: Improved Neural Modeling of Lagrangian Fluid Dynamics
Feb 09, 2024Abstract:Smoothed particle hydrodynamics (SPH) is omnipresent in modern engineering and scientific disciplines. SPH is a class of Lagrangian schemes that discretize fluid dynamics via finite material points that are tracked through the evolving velocity field. Due to the particle-like nature of the simulation, graph neural networks (GNNs) have emerged as appealing and successful surrogates. However, the practical utility of such GNN-based simulators relies on their ability to faithfully model physics, providing accurate and stable predictions over long time horizons - which is a notoriously hard problem. In this work, we identify particle clustering originating from tensile instabilities as one of the primary pitfalls. Based on these insights, we enhance both training and rollout inference of state-of-the-art GNN-based simulators with varying components from standard SPH solvers, including pressure, viscous, and external force components. All neural SPH-enhanced simulators achieve better performance, often by orders of magnitude, than the baseline GNNs, allowing for significantly longer rollouts and significantly better physics modeling. Code available under (https://github.com/tumaer/neuralsph).
JAX-Fluids 2.0: Towards HPC for Differentiable CFD of Compressible Two-phase Flows
Feb 07, 2024Abstract:In our effort to facilitate machine learning-assisted computational fluid dynamics (CFD), we introduce the second iteration of JAX-Fluids. JAX-Fluids is a Python-based fully-differentiable CFD solver designed for compressible single- and two-phase flows. In this work, the first version is extended to incorporate high-performance computing (HPC) capabilities. We introduce a parallelization strategy utilizing JAX primitive operations that scales efficiently on GPU (up to 512 NVIDIA A100 graphics cards) and TPU (up to 1024 TPU v3 cores) HPC systems. We further demonstrate the stable parallel computation of automatic differentiation gradients across extended integration trajectories. The new code version offers enhanced two-phase flow modeling capabilities. In particular, a five-equation diffuse-interface model is incorporated which complements the level-set sharp-interface model. Additional algorithmic improvements include positivity-preserving limiters for increased robustness, support for stretched Cartesian meshes, refactored I/O handling, comprehensive post-processing routines, and an updated list of state-of-the-art high-order numerical discretization schemes. We verify newly added numerical models by showcasing simulation results for single- and two-phase flows, including turbulent boundary layer and channel flows, air-helium shock bubble interactions, and air-water shock drop interactions.
LagrangeBench: A Lagrangian Fluid Mechanics Benchmarking Suite
Sep 28, 2023Abstract:Machine learning has been successfully applied to grid-based PDE modeling in various scientific applications. However, learned PDE solvers based on Lagrangian particle discretizations, which are the preferred approach to problems with free surfaces or complex physics, remain largely unexplored. We present LagrangeBench, the first benchmarking suite for Lagrangian particle problems, focusing on temporal coarse-graining. In particular, our contribution is: (a) seven new fluid mechanics datasets (four in 2D and three in 3D) generated with the Smoothed Particle Hydrodynamics (SPH) method including the Taylor-Green vortex, lid-driven cavity, reverse Poiseuille flow, and dam break, each of which includes different physics like solid wall interactions or free surface, (b) efficient JAX-based API with various recent training strategies and neighbors search routine, and (c) JAX implementation of established Graph Neural Networks (GNNs) like GNS and SEGNN with baseline results. Finally, to measure the performance of learned surrogates we go beyond established position errors and introduce physical metrics like kinetic energy MSE and Sinkhorn distance for the particle distribution. Our codebase is available under the URL: https://github.com/tumaer/lagrangebench
Learning Lagrangian Fluid Mechanics with E($3$)-Equivariant Graph Neural Networks
May 24, 2023Abstract:We contribute to the vastly growing field of machine learning for engineering systems by demonstrating that equivariant graph neural networks have the potential to learn more accurate dynamic-interaction models than their non-equivariant counterparts. We benchmark two well-studied fluid-flow systems, namely 3D decaying Taylor-Green vortex and 3D reverse Poiseuille flow, and evaluate the models based on different performance measures, such as kinetic energy or Sinkhorn distance. In addition, we investigate different embedding methods of physical-information histories for equivariant models. We find that while currently being rather slow to train and evaluate, equivariant models with our proposed history embeddings learn more accurate physical interactions.
On the Relationships between Graph Neural Networks for the Simulation of Physical Systems and Classical Numerical Methods
Mar 31, 2023


Abstract:Recent developments in Machine Learning approaches for modelling physical systems have begun to mirror the past development of numerical methods in the computational sciences. In this survey, we begin by providing an example of this with the parallels between the development trajectories of graph neural network acceleration for physical simulations and particle-based approaches. We then give an overview of simulation approaches, which have not yet found their way into state-of-the-art Machine Learning methods and hold the potential to make Machine Learning approaches more accurate and more efficient. We conclude by presenting an outlook on the potential of these approaches for making Machine Learning models for science more efficient.
E($3$) Equivariant Graph Neural Networks for Particle-Based Fluid Mechanics
Mar 31, 2023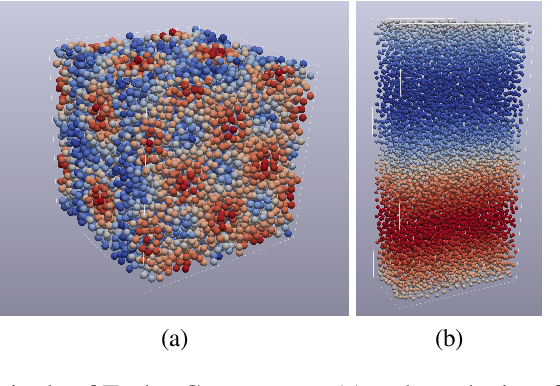
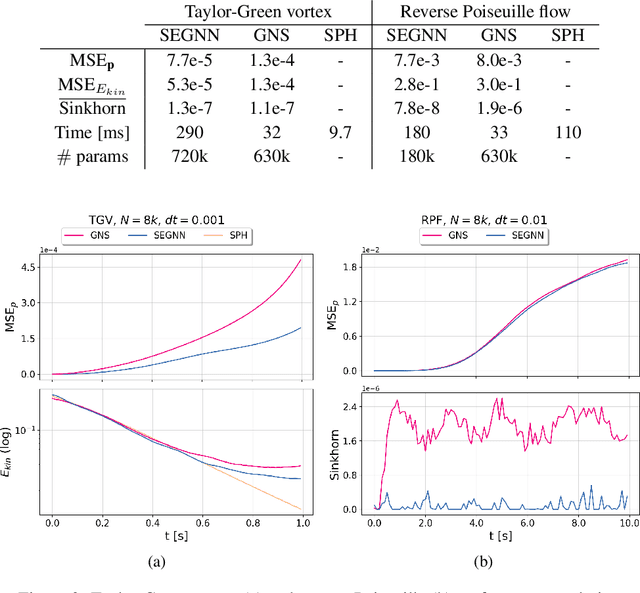
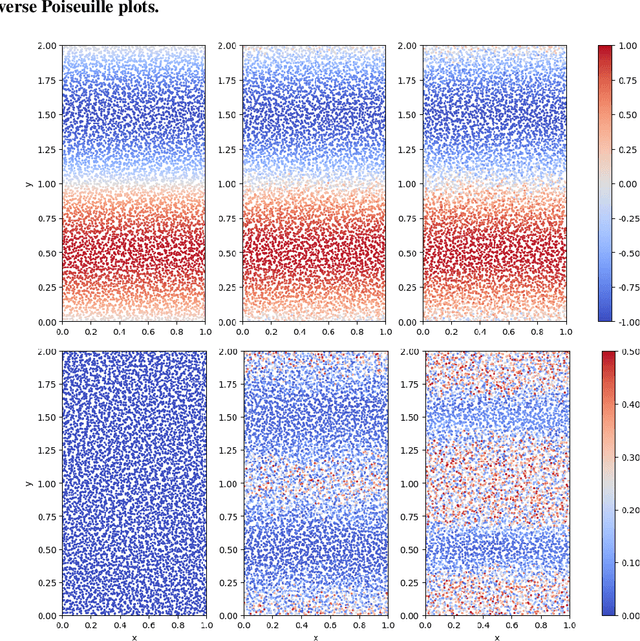
Abstract:We contribute to the vastly growing field of machine learning for engineering systems by demonstrating that equivariant graph neural networks have the potential to learn more accurate dynamic-interaction models than their non-equivariant counterparts. We benchmark two well-studied fluid flow systems, namely the 3D decaying Taylor-Green vortex and the 3D reverse Poiseuille flow, and compare equivariant graph neural networks to their non-equivariant counterparts on different performance measures, such as kinetic energy or Sinkhorn distance. Such measures are typically used in engineering to validate numerical solvers. Our main findings are that while being rather slow to train and evaluate, equivariant models learn more physically accurate interactions. This indicates opportunities for future work towards coarse-grained models for turbulent flows, and generalization across system dynamics and parameters.
JAX-FLUIDS: A fully-differentiable high-order computational fluid dynamics solver for compressible two-phase flows
Mar 25, 2022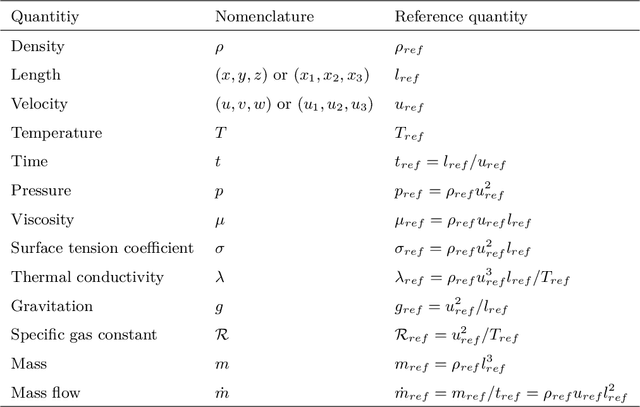

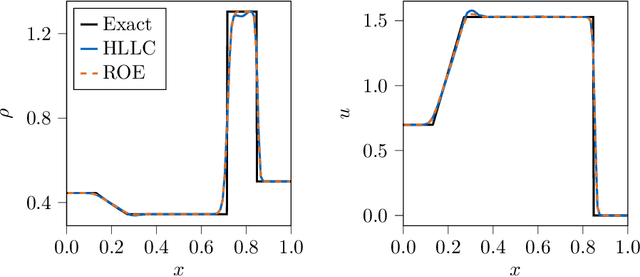
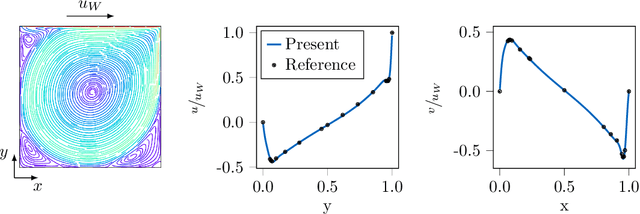
Abstract:Physical systems are governed by partial differential equations (PDEs). The Navier-Stokes equations describe fluid flows and are representative of nonlinear physical systems with complex spatio-temporal interactions. Fluid flows are omnipresent in nature and engineering applications, and their accurate simulation is essential for providing insights into these processes. While PDEs are typically solved with numerical methods, the recent success of machine learning (ML) has shown that ML methods can provide novel avenues of finding solutions to PDEs. ML is becoming more and more present in computational fluid dynamics (CFD). However, up to this date, there does not exist a general-purpose ML-CFD package which provides 1) powerful state-of-the-art numerical methods, 2) seamless hybridization of ML with CFD, and 3) automatic differentiation (AD) capabilities. AD in particular is essential to ML-CFD research as it provides gradient information and enables optimization of preexisting and novel CFD models. In this work, we propose JAX-FLUIDS: a comprehensive fully-differentiable CFD Python solver for compressible two-phase flows. JAX-FLUIDS allows the simulation of complex fluid dynamics with phenomena like three-dimensional turbulence, compressibility effects, and two-phase flows. Written entirely in JAX, it is straightforward to include existing ML models into the proposed framework. Furthermore, JAX-FLUIDS enables end-to-end optimization. I.e., ML models can be optimized with gradients that are backpropagated through the entire CFD algorithm, and therefore contain not only information of the underlying PDE but also of the applied numerical methods. We believe that a Python package like JAX-FLUIDS is crucial to facilitate research at the intersection of ML and CFD and may pave the way for an era of differentiable fluid dynamics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge