LagrangeBench: A Lagrangian Fluid Mechanics Benchmarking Suite

Machine learning has been successfully applied to grid-based PDE modeling in various scientific applications. However, learned PDE solvers based on Lagrangian particle discretizations, which are the preferred approach to problems with free surfaces or complex physics, remain largely unexplored. We present LagrangeBench, the first benchmarking suite for Lagrangian particle problems, focusing on temporal coarse-graining. In particular, our contribution is: (a) seven new fluid mechanics datasets (four in 2D and three in 3D) generated with the Smoothed Particle Hydrodynamics (SPH) method including the Taylor-Green vortex, lid-driven cavity, reverse Poiseuille flow, and dam break, each of which includes different physics like solid wall interactions or free surface, (b) efficient JAX-based API with various recent training strategies and neighbors search routine, and (c) JAX implementation of established Graph Neural Networks (GNNs) like GNS and SEGNN with baseline results. Finally, to measure the performance of learned surrogates we go beyond established position errors and introduce physical metrics like kinetic energy MSE and Sinkhorn distance for the particle distribution. Our codebase is available under the URL: https://github.com/tumaer/lagrangebench

Learning Lagrangian Fluid Mechanics with E($3$)-Equivariant Graph Neural Networks

We contribute to the vastly growing field of machine learning for engineering systems by demonstrating that equivariant graph neural networks have the potential to learn more accurate dynamic-interaction models than their non-equivariant counterparts. We benchmark two well-studied fluid-flow systems, namely 3D decaying Taylor-Green vortex and 3D reverse Poiseuille flow, and evaluate the models based on different performance measures, such as kinetic energy or Sinkhorn distance. In addition, we investigate different embedding methods of physical-information histories for equivariant models. We find that while currently being rather slow to train and evaluate, equivariant models with our proposed history embeddings learn more accurate physical interactions.

E($3$) Equivariant Graph Neural Networks for Particle-Based Fluid Mechanics

We contribute to the vastly growing field of machine learning for engineering systems by demonstrating that equivariant graph neural networks have the potential to learn more accurate dynamic-interaction models than their non-equivariant counterparts. We benchmark two well-studied fluid flow systems, namely the 3D decaying Taylor-Green vortex and the 3D reverse Poiseuille flow, and compare equivariant graph neural networks to their non-equivariant counterparts on different performance measures, such as kinetic energy or Sinkhorn distance. Such measures are typically used in engineering to validate numerical solvers. Our main findings are that while being rather slow to train and evaluate, equivariant models learn more physically accurate interactions. This indicates opportunities for future work towards coarse-grained models for turbulent flows, and generalization across system dynamics and parameters.

Inferring incompressible two-phase flow fields from the interface motion using physics-informed neural networks

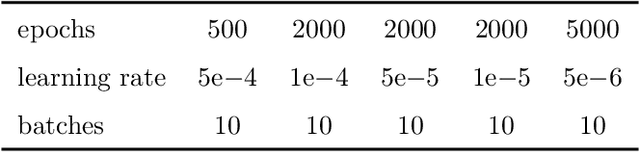
In this work, physics-informed neural networks are applied to incompressible two-phase flow problems. We investigate the forward problem, where the governing equations are solved from initial and boundary conditions, as well as the inverse problem, where continuous velocity and pressure fields are inferred from scattered-time data on the interface position. We employ a volume of fluid approach, i.e. the auxiliary variable here is the volume fraction of the fluids within each phase. For the forward problem, we solve the two-phase Couette and Poiseuille flow. For the inverse problem, three classical test cases for two-phase modeling are investigated: (i) drop in a shear flow, (ii) oscillating drop and (iii) rising bubble. Data of the interface position over time is generated by numerical simulation. An effective way to distribute spatial training points to fit the interface, i.e. the volume fraction field, and the residual points is proposed. Furthermore, we show that appropriate weighting of losses associated with the residual of the partial differential equations is crucial for successful training. The benefit of using adaptive activation functions is evaluated for both the forward and inverse problem.