Rational-WENO: A lightweight, physically-consistent three-point weighted essentially non-oscillatory scheme

Conventional WENO3 methods are known to be highly dissipative at lower resolutions, introducing significant errors in the pre-asymptotic regime. In this paper, we employ a rational neural network to accurately estimate the local smoothness of the solution, dynamically adapting the stencil weights based on local solution features. As rational neural networks can represent fast transitions between smooth and sharp regimes, this approach achieves a granular reconstruction with significantly reduced dissipation, improving the accuracy of the simulation. The network is trained offline on a carefully chosen dataset of analytical functions, bypassing the need for differentiable solvers. We also propose a robust model selection criterion based on estimates of the interpolation's convergence order on a set of test functions, which correlates better with the model performance in downstream tasks. We demonstrate the effectiveness of our approach on several one-, two-, and three-dimensional fluid flow problems: our scheme generalizes across grid resolutions while handling smooth and discontinuous solutions. In most cases, our rational network-based scheme achieves higher accuracy than conventional WENO3 with the same stencil size, and in a few of them, it achieves accuracy comparable to WENO5, which uses a larger stencil.

JAX-Fluids 2.0: Towards HPC for Differentiable CFD of Compressible Two-phase Flows

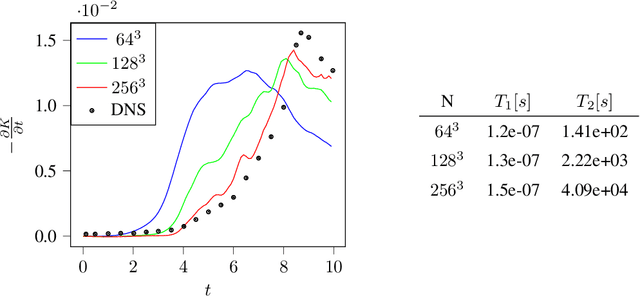
In our effort to facilitate machine learning-assisted computational fluid dynamics (CFD), we introduce the second iteration of JAX-Fluids. JAX-Fluids is a Python-based fully-differentiable CFD solver designed for compressible single- and two-phase flows. In this work, the first version is extended to incorporate high-performance computing (HPC) capabilities. We introduce a parallelization strategy utilizing JAX primitive operations that scales efficiently on GPU (up to 512 NVIDIA A100 graphics cards) and TPU (up to 1024 TPU v3 cores) HPC systems. We further demonstrate the stable parallel computation of automatic differentiation gradients across extended integration trajectories. The new code version offers enhanced two-phase flow modeling capabilities. In particular, a five-equation diffuse-interface model is incorporated which complements the level-set sharp-interface model. Additional algorithmic improvements include positivity-preserving limiters for increased robustness, support for stretched Cartesian meshes, refactored I/O handling, comprehensive post-processing routines, and an updated list of state-of-the-art high-order numerical discretization schemes. We verify newly added numerical models by showcasing simulation results for single- and two-phase flows, including turbulent boundary layer and channel flows, air-helium shock bubble interactions, and air-water shock drop interactions.

JAX-FLUIDS: A fully-differentiable high-order computational fluid dynamics solver for compressible two-phase flows

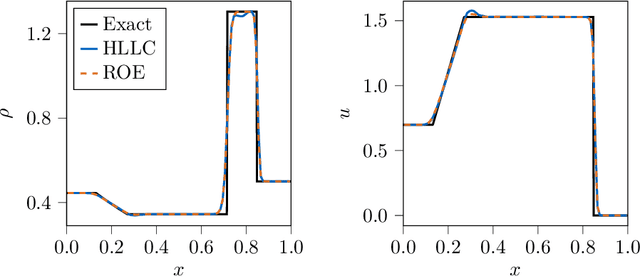
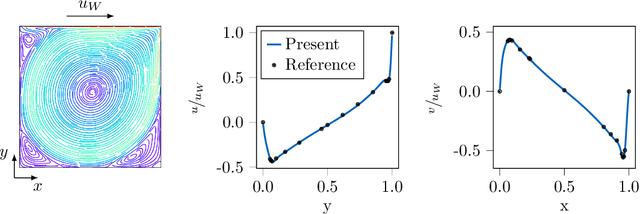
Physical systems are governed by partial differential equations (PDEs). The Navier-Stokes equations describe fluid flows and are representative of nonlinear physical systems with complex spatio-temporal interactions. Fluid flows are omnipresent in nature and engineering applications, and their accurate simulation is essential for providing insights into these processes. While PDEs are typically solved with numerical methods, the recent success of machine learning (ML) has shown that ML methods can provide novel avenues of finding solutions to PDEs. ML is becoming more and more present in computational fluid dynamics (CFD). However, up to this date, there does not exist a general-purpose ML-CFD package which provides 1) powerful state-of-the-art numerical methods, 2) seamless hybridization of ML with CFD, and 3) automatic differentiation (AD) capabilities. AD in particular is essential to ML-CFD research as it provides gradient information and enables optimization of preexisting and novel CFD models. In this work, we propose JAX-FLUIDS: a comprehensive fully-differentiable CFD Python solver for compressible two-phase flows. JAX-FLUIDS allows the simulation of complex fluid dynamics with phenomena like three-dimensional turbulence, compressibility effects, and two-phase flows. Written entirely in JAX, it is straightforward to include existing ML models into the proposed framework. Furthermore, JAX-FLUIDS enables end-to-end optimization. I.e., ML models can be optimized with gradients that are backpropagated through the entire CFD algorithm, and therefore contain not only information of the underlying PDE but also of the applied numerical methods. We believe that a Python package like JAX-FLUIDS is crucial to facilitate research at the intersection of ML and CFD and may pave the way for an era of differentiable fluid dynamics.

A fully-differentiable compressible high-order computational fluid dynamics solver

Fluid flows are omnipresent in nature and engineering disciplines. The reliable computation of fluids has been a long-lasting challenge due to nonlinear interactions over multiple spatio-temporal scales. The compressible Navier-Stokes equations govern compressible flows and allow for complex phenomena like turbulence and shocks. Despite tremendous progress in hardware and software, capturing the smallest length-scales in fluid flows still introduces prohibitive computational cost for real-life applications. We are currently witnessing a paradigm shift towards machine learning supported design of numerical schemes as a means to tackle aforementioned problem. While prior work has explored differentiable algorithms for one- or two-dimensional incompressible fluid flows, we present a fully-differentiable three-dimensional framework for the computation of compressible fluid flows using high-order state-of-the-art numerical methods. Firstly, we demonstrate the efficiency of our solver by computing classical two- and three-dimensional test cases, including strong shocks and transition to turbulence. Secondly, and more importantly, our framework allows for end-to-end optimization to improve existing numerical schemes inside computational fluid dynamics algorithms. In particular, we are using neural networks to substitute a conventional numerical flux function.

Consistent and symmetry preserving data-driven interface reconstruction for the level-set method

Recently, machine learning has been used to substitute parts of conventional computational fluid dynamics, e.g. the cell-face reconstruction in finite-volume solvers or the curvature computation in the Volume-of-Fluid (VOF) method. The latter showed improvements in terms of accuracy for coarsely resolved interfaces, however at the expense of convergence and symmetry. In this work, a combined approach is proposed, adressing the aforementioned shortcomings. We focus on interface reconstruction (IR) in the level-set method, i.e. the computation of the volume fraction and apertures. The combined model consists of a classification neural network, that chooses between the conventional (linear) IR and the neural network IR depending on the local interface resolution. The proposed approach improves accuracy for coarsely resolved interfaces and recovers the conventional IR for high resolutions, yielding first order overall convergence. Symmetry is preserved by mirroring and rotating the input level-set grid and subsequently averaging the predictions. The combined model is implemented into a CFD solver and demonstrated for two-phase flows. Furthermore, we provide details of floating point symmetric implementation and computational efficiency.

Inferring incompressible two-phase flow fields from the interface motion using physics-informed neural networks

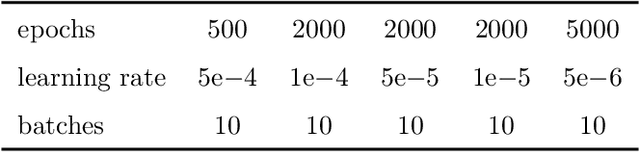
In this work, physics-informed neural networks are applied to incompressible two-phase flow problems. We investigate the forward problem, where the governing equations are solved from initial and boundary conditions, as well as the inverse problem, where continuous velocity and pressure fields are inferred from scattered-time data on the interface position. We employ a volume of fluid approach, i.e. the auxiliary variable here is the volume fraction of the fluids within each phase. For the forward problem, we solve the two-phase Couette and Poiseuille flow. For the inverse problem, three classical test cases for two-phase modeling are investigated: (i) drop in a shear flow, (ii) oscillating drop and (iii) rising bubble. Data of the interface position over time is generated by numerical simulation. An effective way to distribute spatial training points to fit the interface, i.e. the volume fraction field, and the residual points is proposed. Furthermore, we show that appropriate weighting of losses associated with the residual of the partial differential equations is crucial for successful training. The benefit of using adaptive activation functions is evaluated for both the forward and inverse problem.