HydroGym: A Reinforcement Learning Platform for Fluid Dynamics

Modeling and controlling fluid flows is critical for several fields of science and engineering, including transportation, energy, and medicine. Effective flow control can lead to, e.g., lift increase, drag reduction, mixing enhancement, and noise reduction. However, controlling a fluid faces several significant challenges, including high-dimensional, nonlinear, and multiscale interactions in space and time. Reinforcement learning (RL) has recently shown great success in complex domains, such as robotics and protein folding, but its application to flow control is hindered by a lack of standardized benchmark platforms and the computational demands of fluid simulations. To address these challenges, we introduce HydroGym, a solver-independent RL platform for flow control research. HydroGym integrates sophisticated flow control benchmarks, scalable runtime infrastructure, and state-of-the-art RL algorithms. Our platform includes 42 validated environments spanning from canonical laminar flows to complex three-dimensional turbulent scenarios, validated over a wide range of Reynolds numbers. We provide non-differentiable solvers for traditional RL and differentiable solvers that dramatically improve sample efficiency through gradient-enhanced optimization. Comprehensive evaluation reveals that RL agents consistently discover robust control principles across configurations, such as boundary layer manipulation, acoustic feedback disruption, and wake reorganization. Transfer learning studies demonstrate that controllers learned at one Reynolds number or geometry adapt efficiently to new conditions, requiring approximately 50% fewer training episodes. The HydroGym platform is highly extensible and scalable, providing a framework for researchers in fluid dynamics, machine learning, and control to add environments, surrogate models, and control algorithms to advance science and technology.

Physics-informed neural networks for inverse problems in supersonic flows

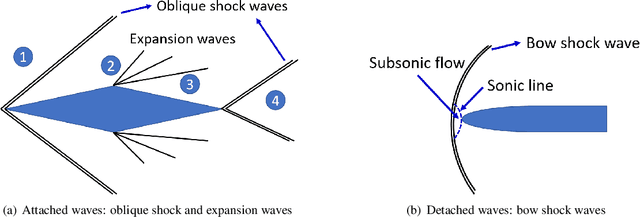
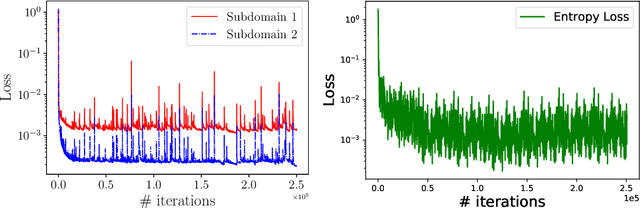
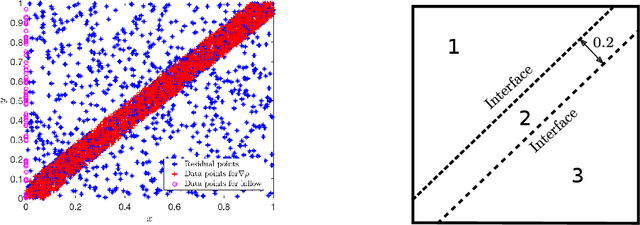
Accurate solutions to inverse supersonic compressible flow problems are often required for designing specialized aerospace vehicles. In particular, we consider the problem where we have data available for density gradients from Schlieren photography as well as data at the inflow and part of wall boundaries. These inverse problems are notoriously difficult and traditional methods may not be adequate to solve such ill-posed inverse problems. To this end, we employ the physics-informed neural networks (PINNs) and its extended version, extended PINNs (XPINNs), where domain decomposition allows deploying locally powerful neural networks in each subdomain, which can provide additional expressivity in subdomains, where a complex solution is expected. Apart from the governing compressible Euler equations, we also enforce the entropy conditions in order to obtain viscosity solutions. Moreover, we enforce positivity conditions on density and pressure. We consider inverse problems involving two-dimensional expansion waves, two-dimensional oblique and bow shock waves. We compare solutions obtained by PINNs and XPINNs and invoke some theoretical results that can be used to decide on the generalization errors of the two methods.

Consistent and symmetry preserving data-driven interface reconstruction for the level-set method

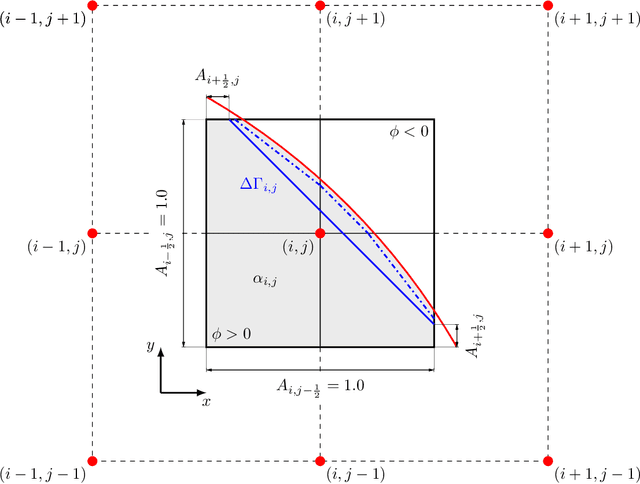
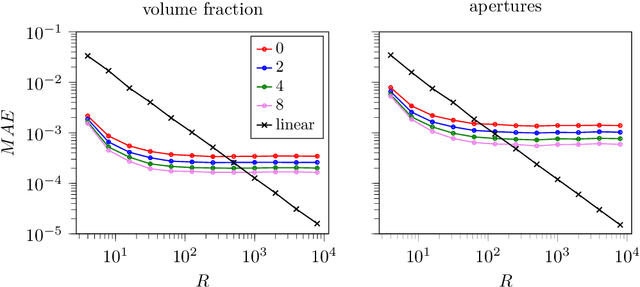
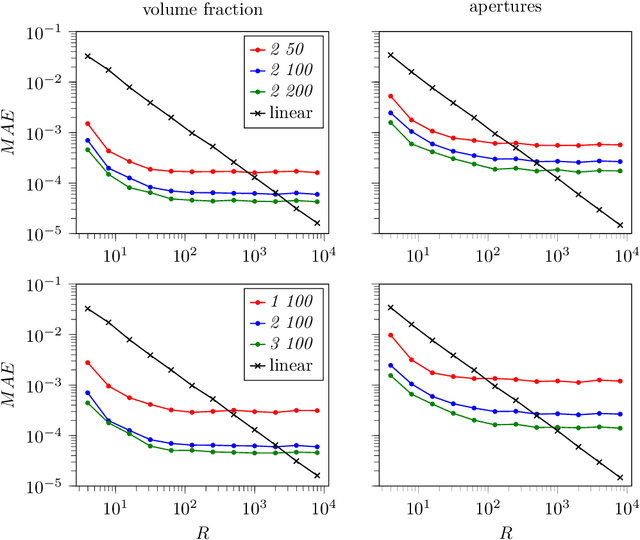
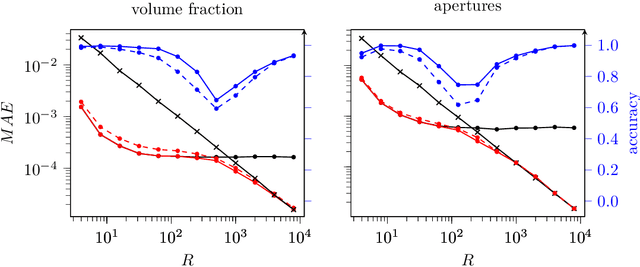
Recently, machine learning has been used to substitute parts of conventional computational fluid dynamics, e.g. the cell-face reconstruction in finite-volume solvers or the curvature computation in the Volume-of-Fluid (VOF) method. The latter showed improvements in terms of accuracy for coarsely resolved interfaces, however at the expense of convergence and symmetry. In this work, a combined approach is proposed, adressing the aforementioned shortcomings. We focus on interface reconstruction (IR) in the level-set method, i.e. the computation of the volume fraction and apertures. The combined model consists of a classification neural network, that chooses between the conventional (linear) IR and the neural network IR depending on the local interface resolution. The proposed approach improves accuracy for coarsely resolved interfaces and recovers the conventional IR for high resolutions, yielding first order overall convergence. Symmetry is preserved by mirroring and rotating the input level-set grid and subsequently averaging the predictions. The combined model is implemented into a CFD solver and demonstrated for two-phase flows. Furthermore, we provide details of floating point symmetric implementation and computational efficiency.