E($3$) Equivariant Graph Neural Networks for Particle-Based Fluid Mechanics
Paper and Code
Mar 31, 2023
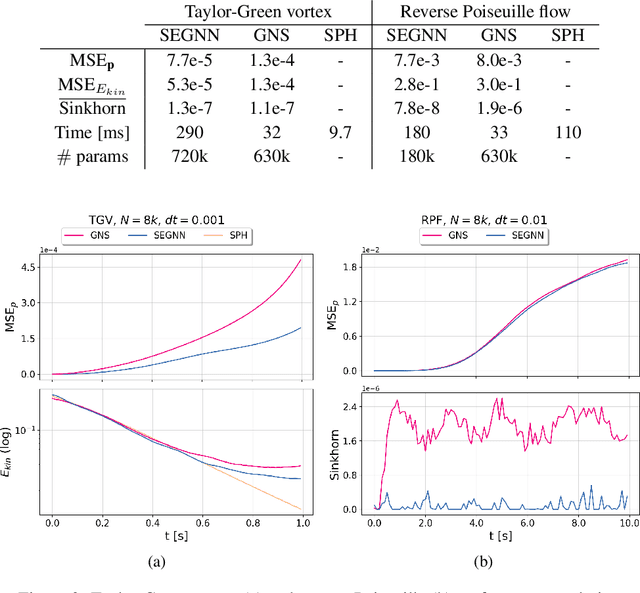
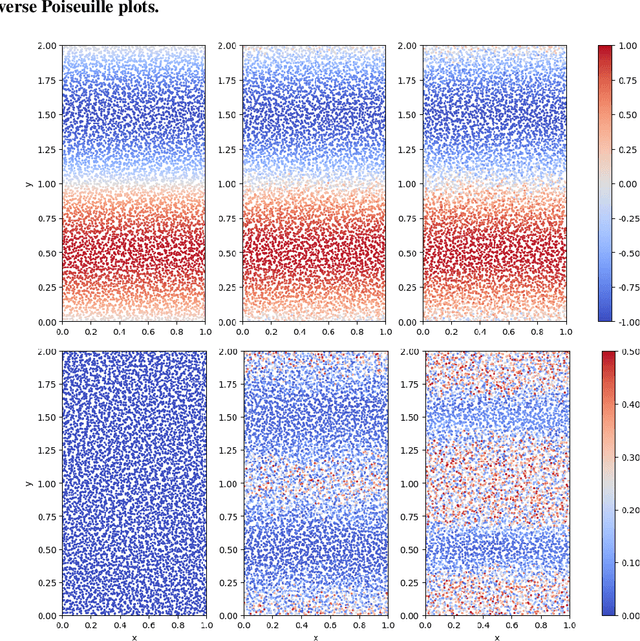
We contribute to the vastly growing field of machine learning for engineering systems by demonstrating that equivariant graph neural networks have the potential to learn more accurate dynamic-interaction models than their non-equivariant counterparts. We benchmark two well-studied fluid flow systems, namely the 3D decaying Taylor-Green vortex and the 3D reverse Poiseuille flow, and compare equivariant graph neural networks to their non-equivariant counterparts on different performance measures, such as kinetic energy or Sinkhorn distance. Such measures are typically used in engineering to validate numerical solvers. Our main findings are that while being rather slow to train and evaluate, equivariant models learn more physically accurate interactions. This indicates opportunities for future work towards coarse-grained models for turbulent flows, and generalization across system dynamics and parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge