Representation-Aligned Tactile Grounding for Contact-Rich Robotic Manipulation

Tactile-enhanced vision-language-action (VLA) policies have been introduced for contact-rich manipulation, where critical interaction states are often hidden from vision. Future tactile prediction is a promising way to use touch because it turns tactile outcomes into supervision for action-induced contact dynamics. Yet VLA policies contain representations with different roles, from perceptual encoding to motor prediction, making it unclear where this supervision should be applied. We study this as a representation-alignment problem. Through a linear probe analysis, we find that future tactile states are most predictable from intermediate action-expert features, rather than from vision-language features or final action states. Motivated by this observation, we introduce a lightweight Latent Tactile Predictor (LTP), which predicts compact future tactile embeddings from the identified intermediate representation. By avoiding direct prediction of noisy raw tactile signals, LTP provides an action-outcome grounding signal that aligns intermediate action representations with future contact consequences. Experiments on real-world contact-rich manipulation tasks show that representation-aligned tactile grounding outperforms less aligned or multi-interface tactile prediction, highlighting the importance of where tactile supervision is applied.

Method of data forward generation with partial differential equations for machine learning modeling in fluid mechanics

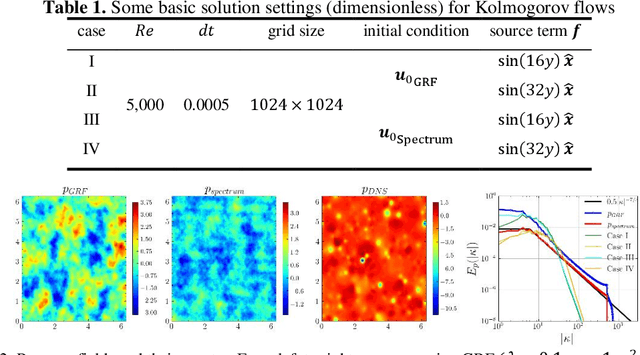
Artificial intelligence (AI) for fluid mechanics has become attractive topic. High-fidelity data is one of most critical issues for the successful applications of AI in fluid mechanics, however, it is expensively obtained or even inaccessible. This study proposes a high-efficient data forward generation method from the partial differential equations (PDEs). Specifically, the solutions of the PDEs are first generated either following a random field (e.g. Gaussian random field, GRF, computational complexity O(NlogN), N is the number of spatial points) or physical laws (e.g. a kind of spectra, computational complexity O(NM), M is the number of modes), then the source terms, boundary conditions and initial conditions are computed to satisfy PDEs. Thus, the data pairs of source terms, boundary conditions and initial conditions with corresponding solutions of PDEs can be constructed. A Poisson neural network (Poisson-NN) embedded in projection method and a wavelet transform convolutional neuro network (WTCNN) embedded in multigrid numerical simulation for solving incompressible Navier-Stokes equations is respectively proposed. The feasibility of generated data for training Poisson-NN and WTCNN is validated. The results indicate that even without any DNS data, the generated data can train these two models with excellent generalization and accuracy. The data following physical laws can significantly improve the convergence rate, generalization and accuracy than that generated following GRF.