Xiaowei Jin
Application-Driven Value Alignment in Agentic AI Systems: Survey and Perspectives
Jun 11, 2025Abstract:The ongoing evolution of AI paradigms has propelled AI research into the Agentic AI stage. Consequently, the focus of research has shifted from single agents and simple applications towards multi-agent autonomous decision-making and task collaboration in complex environments. As Large Language Models (LLMs) advance, their applications become more diverse and complex, leading to increasingly situational and systemic risks. This has brought significant attention to value alignment for AI agents, which aims to ensure that an agent's goals, preferences, and behaviors align with human values and societal norms. This paper reviews value alignment in agent systems within specific application scenarios. It integrates the advancements in AI driven by large models with the demands of social governance. Our review covers value principles, agent system application scenarios, and agent value alignment evaluation. Specifically, value principles are organized hierarchically from a top-down perspective, encompassing macro, meso, and micro levels. Agent system application scenarios are categorized and reviewed from a general-to-specific viewpoint. Agent value alignment evaluation systematically examines datasets for value alignment assessment and relevant value alignment methods. Additionally, we delve into value coordination among multiple agents within agent systems. Finally, we propose several potential research directions in this field.
Spatiotemporal Field Generation Based on Hybrid Mamba-Transformer with Physics-informed Fine-tuning
May 16, 2025Abstract:This research confronts the challenge of substantial physical equation discrepancies encountered in the generation of spatiotemporal physical fields through data-driven trained models. A spatiotemporal physical field generation model, named HMT-PF, is developed based on the hybrid Mamba-Transformer architecture, incorporating unstructured grid information as input. A fine-tuning block, enhanced with physical information, is introduced to effectively reduce the physical equation discrepancies. The physical equation residuals are computed through a point query mechanism for efficient gradient evaluation, then encoded into latent space for refinement. The fine-tuning process employs a self-supervised learning approach to achieve physical consistency while maintaining essential field characteristics. Results show that the hybrid Mamba-Transformer model achieves good performance in generating spatiotemporal fields, while the physics-informed fine-tuning mechanism further reduces significant physical errors effectively. A MSE-R evaluation method is developed to assess the accuracy and realism of physical field generation.
Method of data forward generation with partial differential equations for machine learning modeling in fluid mechanics
Jan 06, 2025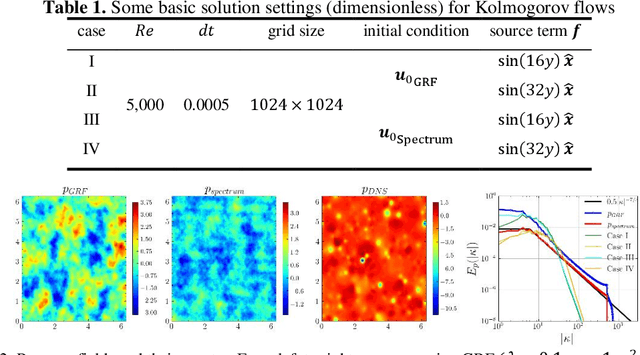



Abstract:Artificial intelligence (AI) for fluid mechanics has become attractive topic. High-fidelity data is one of most critical issues for the successful applications of AI in fluid mechanics, however, it is expensively obtained or even inaccessible. This study proposes a high-efficient data forward generation method from the partial differential equations (PDEs). Specifically, the solutions of the PDEs are first generated either following a random field (e.g. Gaussian random field, GRF, computational complexity O(NlogN), N is the number of spatial points) or physical laws (e.g. a kind of spectra, computational complexity O(NM), M is the number of modes), then the source terms, boundary conditions and initial conditions are computed to satisfy PDEs. Thus, the data pairs of source terms, boundary conditions and initial conditions with corresponding solutions of PDEs can be constructed. A Poisson neural network (Poisson-NN) embedded in projection method and a wavelet transform convolutional neuro network (WTCNN) embedded in multigrid numerical simulation for solving incompressible Navier-Stokes equations is respectively proposed. The feasibility of generated data for training Poisson-NN and WTCNN is validated. The results indicate that even without any DNS data, the generated data can train these two models with excellent generalization and accuracy. The data following physical laws can significantly improve the convergence rate, generalization and accuracy than that generated following GRF.
An invariance constrained deep learning network for PDE discovery
Feb 06, 2024Abstract:The discovery of partial differential equations (PDEs) from datasets has attracted increased attention. However, the discovery of governing equations from sparse data with high noise is still very challenging due to the difficulty of derivatives computation and the disturbance of noise. Moreover, the selection principles for the candidate library to meet physical laws need to be further studied. The invariance is one of the fundamental laws for governing equations. In this study, we propose an invariance constrained deep learning network (ICNet) for the discovery of PDEs. Considering that temporal and spatial translation invariance (Galilean invariance) is a fundamental property of physical laws, we filter the candidates that cannot meet the requirement of the Galilean transformations. Subsequently, we embedded the fixed and possible terms into the loss function of neural network, significantly countering the effect of sparse data with high noise. Then, by filtering out redundant terms without fixing learnable parameters during the training process, the governing equations discovered by the ICNet method can effectively approximate the real governing equations. We select the 2D Burgers equation, the equation of 2D channel flow over an obstacle, and the equation of 3D intracranial aneurysm as examples to verify the superiority of the ICNet for fluid mechanics. Furthermore, we extend similar invariance methods to the discovery of wave equation (Lorentz Invariance) and verify it through Single and Coupled Klein-Gordon equation. The results show that the ICNet method with physical constraints exhibits excellent performance in governing equations discovery from sparse and noisy data.
Discovering Governing Equations by Machine Learning implemented with Invariance
Mar 29, 2022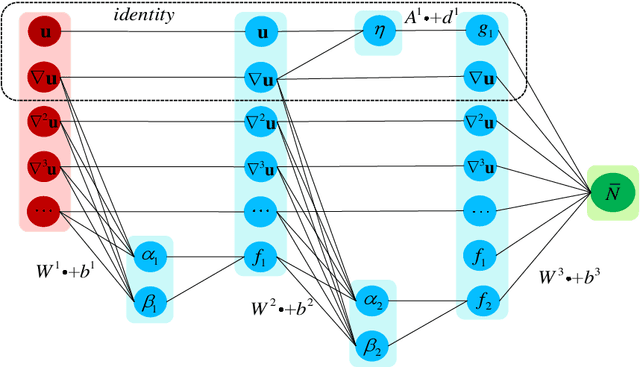



Abstract:The partial differential equation (PDE) plays a significantly important role in many fields of science and engineering. The conventional case of the derivation of PDE mainly relies on first principles and empirical observation. However, the development of machine learning technology allows us to mine potential control equations from the massive amounts of stored data in a fresh way. Although there has been considerable progress in the data-driven discovery of PDE, the extant literature mostly focuses on the improvements of discovery methods, without substantial breakthroughs in the discovery process itself, including the principles for the construction of candidates and how to incorporate physical priors. In this paper, through rigorous derivation of formulas, novel physically enhanced machining learning discovery methods for control equations: GSNN (Galileo Symbolic Neural Network) and LSNN (Lorentz Symbolic Neural Network) are firstly proposed based on Galileo invariance and Lorentz invariance respectively, setting forth guidelines for building the candidates of discovering equations. The adoption of mandatory embedding of physical constraints is fundamentally different from PINN in the form of the loss function, thus ensuring that the designed Neural Network strictly obeys the physical prior of invariance and enhancing the interpretability of the network. By comparing the results with PDE-NET in numerical experiments of Burgers equation and Sine-Gordon equation, it shows that the method presented in this study has better accuracy, parsimony, and interpretability.
General solutions for nonlinear differential equations: a deep reinforcement learning approach
May 13, 2018



Abstract:Physicists use differential equations to describe the physical dynamical world, and the solutions of these equations constitute our understanding of the world. During the hundreds of years, scientists developed several ways to solve these equations, i.e., the analytical solutions and the numerical solutions. However, for some complex equations, there may be no analytical solutions, and the numerical solutions may encounter the curse of the extreme computational cost if the accuracy is the first consideration. Solving equations is a high-level human intelligence work and a crucial step towards general artificial intelligence (AI), where deep reinforcement learning (DRL) may contribute. This work makes the first attempt of applying (DRL) to solve nonlinear differential equations both in discretized and continuous format with the governing equations (physical laws) embedded in the DRL network, including ordinary differential equations (ODEs) and partial differential equations (PDEs). The DRL network consists of an actor that outputs solution approximations policy and a critic that outputs the critic of the actor's output solution. Deterministic policy network is employed as the actor, and governing equations are embedded in the critic. The effectiveness of the DRL solver in Schr\"odinger equation, Navier-Stocks, Van der Pol equation, Burgers' equation and the equation of motion are discussed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge