Yi-fan Chen
Neural Ideal Large Eddy Simulation: Modeling Turbulence with Neural Stochastic Differential Equations
Jun 01, 2023



Abstract:We introduce a data-driven learning framework that assimilates two powerful ideas: ideal large eddy simulation (LES) from turbulence closure modeling and neural stochastic differential equations (SDE) for stochastic modeling. The ideal LES models the LES flow by treating each full-order trajectory as a random realization of the underlying dynamics, as such, the effect of small-scales is marginalized to obtain the deterministic evolution of the LES state. However, ideal LES is analytically intractable. In our work, we use a latent neural SDE to model the evolution of the stochastic process and an encoder-decoder pair for transforming between the latent space and the desired ideal flow field. This stands in sharp contrast to other types of neural parameterization of closure models where each trajectory is treated as a deterministic realization of the dynamics. We show the effectiveness of our approach (niLES - neural ideal LES) on a challenging chaotic dynamical system: Kolmogorov flow at a Reynolds number of 20,000. Compared to competing methods, our method can handle non-uniform geometries using unstructured meshes seamlessly. In particular, niLES leads to trajectories with more accurate statistics and enhances stability, particularly for long-horizon rollouts.
Debias Coarsely, Sample Conditionally: Statistical Downscaling through Optimal Transport and Probabilistic Diffusion Models
May 24, 2023



Abstract:We introduce a two-stage probabilistic framework for statistical downscaling between unpaired data. Statistical downscaling seeks a probabilistic map to transform low-resolution data from a (possibly biased) coarse-grained numerical scheme to high-resolution data that is consistent with a high-fidelity scheme. Our framework tackles the problem by tandeming two transformations: a debiasing step that is performed by an optimal transport map, and an upsampling step that is achieved by a probabilistic diffusion model with \textit{a posteriori} conditional sampling. This approach characterizes a conditional distribution without the need for paired data, and faithfully recovers relevant physical statistics from biased samples. We demonstrate the utility of the proposed approach on one- and two-dimensional fluid flow problems, which are representative of the core difficulties present in numerical simulations of weather and climate. Our method produces realistic high-resolution outputs from low-resolution inputs, by upsampling resolutions of $8\times$ and $16\times$. Moreover, our procedure correctly matches the statistics of physical quantities, even when the low-frequency content of the inputs and outputs do not match, a crucial but difficult-to-satisfy assumption needed by current state-of-the-art alternatives.
Policy Learning and Evaluation with Randomized Quasi-Monte Carlo
Feb 21, 2022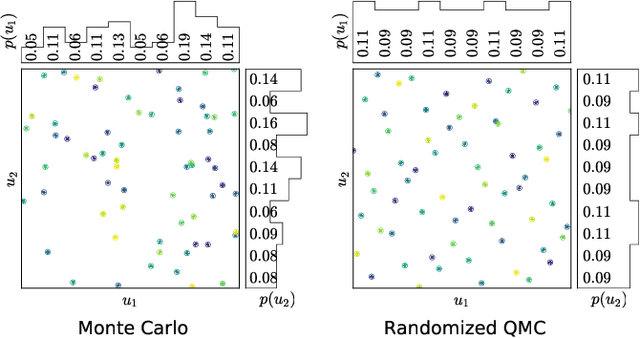
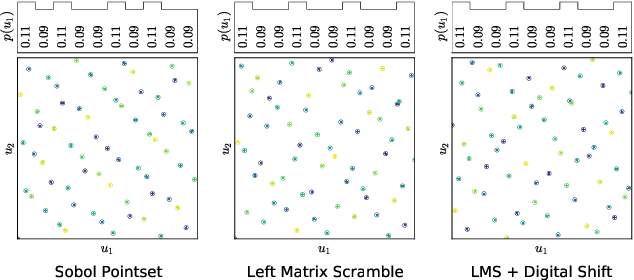
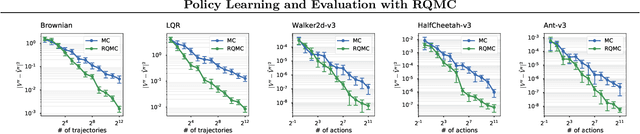
Abstract:Reinforcement learning constantly deals with hard integrals, for example when computing expectations in policy evaluation and policy iteration. These integrals are rarely analytically solvable and typically estimated with the Monte Carlo method, which induces high variance in policy values and gradients. In this work, we propose to replace Monte Carlo samples with low-discrepancy point sets. We combine policy gradient methods with Randomized Quasi-Monte Carlo, yielding variance-reduced formulations of policy gradient and actor-critic algorithms. These formulations are effective for policy evaluation and policy improvement, as they outperform state-of-the-art algorithms on standardized continuous control benchmarks. Our empirical analyses validate the intuition that replacing Monte Carlo with Quasi-Monte Carlo yields significantly more accurate gradient estimates.
HyperPINN: Learning parameterized differential equations with physics-informed hypernetworks
Oct 28, 2021
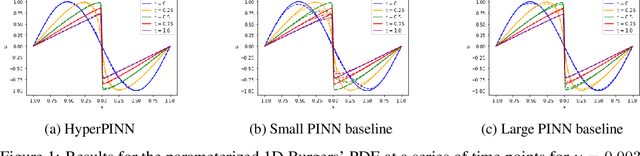
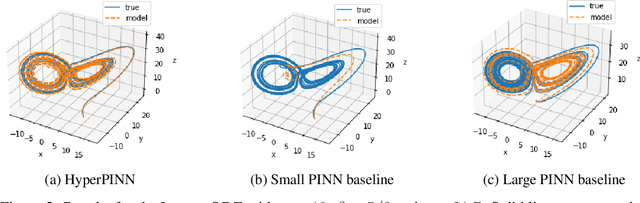

Abstract:Many types of physics-informed neural network models have been proposed in recent years as approaches for learning solutions to differential equations. When a particular task requires solving a differential equation at multiple parameterizations, this requires either re-training the model, or expanding its representation capacity to include the parameterization -- both solution that increase its computational cost. We propose the HyperPINN, which uses hypernetworks to learn to generate neural networks that can solve a differential equation from a given parameterization. We demonstrate with experiments on both a PDE and an ODE that this type of model can lead to neural network solutions to differential equations that maintain a small size, even when learning a family of solutions over a parameter space.
End-to-End Jet Classification of Boosted Top Quarks with the CMS Open Data
Apr 19, 2021
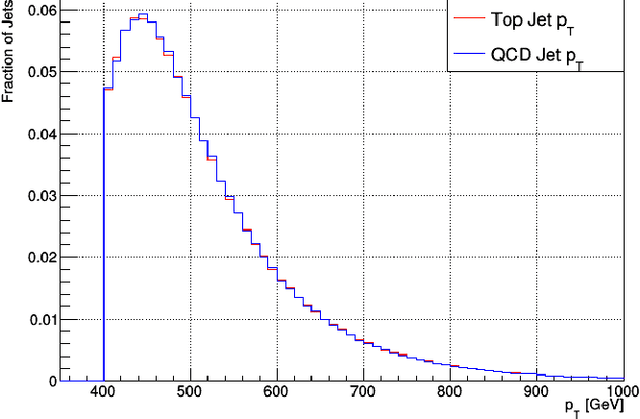
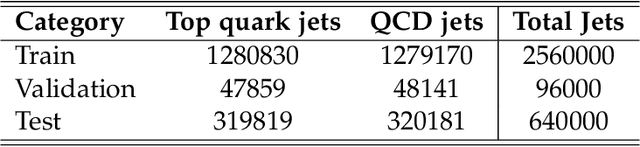
Abstract:We describe a novel application of the end-to-end deep learning technique to the task of discriminating top quark-initiated jets from those originating from the hadronization of a light quark or a gluon. The end-to-end deep learning technique combines deep learning algorithms and low-level detector representation of the high-energy collision event. In this study, we use low-level detector information from the simulated CMS Open Data samples to construct the top jet classifiers. To optimize classifier performance we progressively add low-level information from the CMS tracking detector, including pixel detector reconstructed hits and impact parameters, and demonstrate the value of additional tracking information even when no new spatial structures are added. Relying only on calorimeter energy deposits and reconstructed pixel detector hits, the end-to-end classifier achieves an AUC score of 0.975$\pm$0.002 for the task of classifying boosted top quark jets. After adding derived track quantities, the classifier AUC score increases to 0.9824$\pm$0.0013, serving as the first performance benchmark for these CMS Open Data samples. We additionally provide a timing performance comparison of different processor unit architectures for training the network.
Simulation Pipeline for Traffic Evacuation in Urban Areas and Emergency Traffic Management Policy Improvements
Feb 14, 2020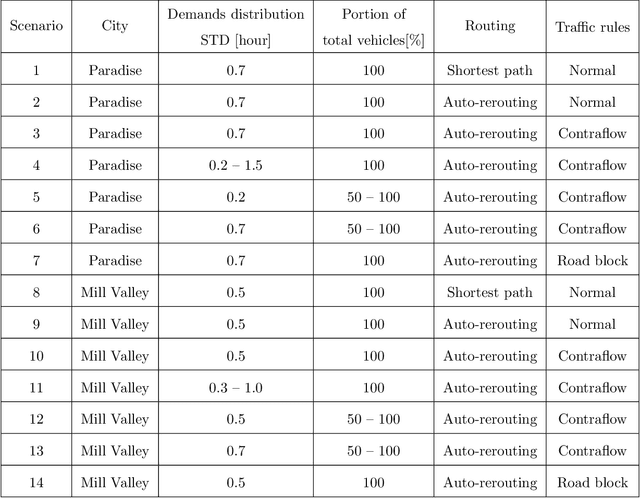
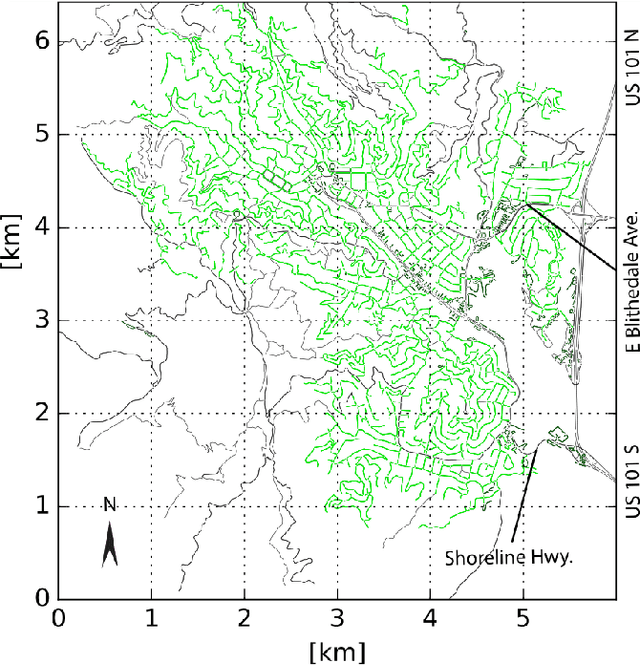
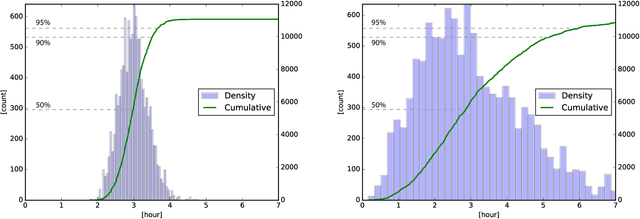
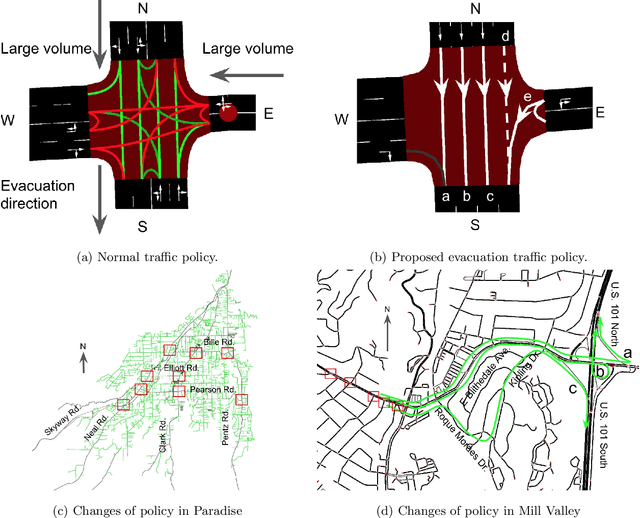
Abstract:Traffic evacuation plays a critical role in saving lives in devastating disasters such as hurricanes, wildfires, floods, earthquakes, etc. An ability to evaluate evacuation plans in advance for these rare events, including identifying traffic flow bottlenecks, improving traffic management policies, and understanding the robustness of the traffic management policy are critical for emergency management. Given the rareness of such events and the corresponding lack of real data, traffic simulation provides a flexible and versatile approach for such scenarios, and furthermore allows dynamic interaction with the simulated evacuation. In this paper, we build a traffic simulation pipeline to explore the above problems, covering many aspects of evacuation, including map creation, demand generation, vehicle behavior, bottleneck identification, traffic management policy improvement, and results analysis. We apply the pipeline to two case studies in California. The first is Paradise, which was destroyed by a large wildfire in 2018 and experienced catastrophic traffic jams during the evacuation. The second is Mill Valley, which has high risk of wildfire and potential traffic issues since the city is situated in a narrow valley.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge