FlowLensing: Simulating Gravitational Lensing with Flow Matching

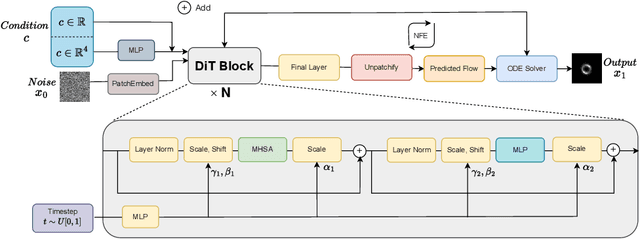
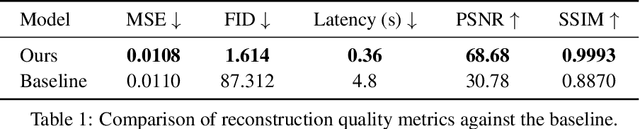
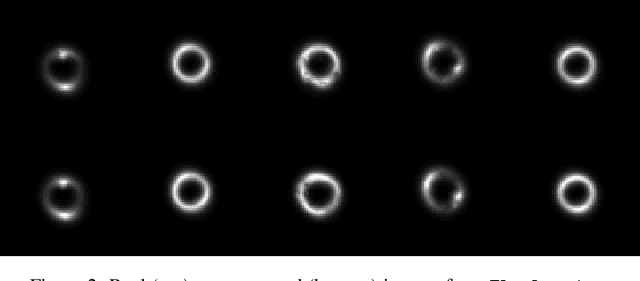
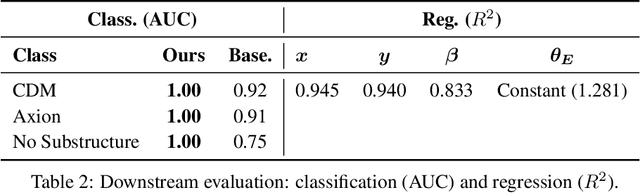
Gravitational lensing is one of the most powerful probes of dark matter, yet creating high-fidelity lensed images at scale remains a bottleneck. Existing tools rely on ray-tracing or forward-modeling pipelines that, while precise, are prohibitively slow. We introduce FlowLensing, a Diffusion Transformer-based compact and efficient flow-matching model for strong gravitational lensing simulation. FlowLensing operates in both discrete and continuous regimes, handling classes such as different dark matter models as well as continuous model parameters ensuring physical consistency. By enabling scalable simulations, our model can advance dark matter studies, specifically for probing dark matter substructure in cosmological surveys. We find that our model achieves a speedup of over 200$\times$ compared to classical simulators for intensive dark matter models, with high fidelity and low inference latency. FlowLensing enables rapid, scalable, and physically consistent image synthesis, offering a practical alternative to traditional forward-modeling pipelines.

Sinusoidal Approximation Theorem for Kolmogorov-Arnold Networks

The Kolmogorov-Arnold representation theorem states that any continuous multivariable function can be exactly represented as a finite superposition of continuous single variable functions. Subsequent simplifications of this representation involve expressing these functions as parameterized sums of a smaller number of unique monotonic functions. These developments led to the proof of the universal approximation capabilities of multilayer perceptron networks with sigmoidal activations, forming the alternative theoretical direction of most modern neural networks. Kolmogorov-Arnold Networks (KANs) have been recently proposed as an alternative to multilayer perceptrons. KANs feature learnable nonlinear activations applied directly to input values, modeled as weighted sums of basis spline functions. This approach replaces the linear transformations and sigmoidal post-activations used in traditional perceptrons. Subsequent works have explored alternatives to spline-based activations. In this work, we propose a novel KAN variant by replacing both the inner and outer functions in the Kolmogorov-Arnold representation with weighted sinusoidal functions of learnable frequencies. Inspired by simplifications introduced by Lorentz and Sprecher, we fix the phases of the sinusoidal activations to linearly spaced constant values and provide a proof of its theoretical validity. We also conduct numerical experiments to evaluate its performance on a range of multivariable functions, comparing it with fixed-frequency Fourier transform methods and multilayer perceptrons (MLPs). We show that it outperforms the fixed-frequency Fourier transform and achieves comparable performance to MLPs.

Quantum Diffusion Model for Quark and Gluon Jet Generation

Diffusion models have demonstrated remarkable success in image generation, but they are computationally intensive and time-consuming to train. In this paper, we introduce a novel diffusion model that benefits from quantum computing techniques in order to mitigate computational challenges and enhance generative performance within high energy physics data. The fully quantum diffusion model replaces Gaussian noise with random unitary matrices in the forward process and incorporates a variational quantum circuit within the U-Net in the denoising architecture. We run evaluations on the structurally complex quark and gluon jets dataset from the Large Hadron Collider. The results demonstrate that the fully quantum and hybrid models are competitive with a similar classical model for jet generation, highlighting the potential of using quantum techniques for machine learning problems.

Lie-Equivariant Quantum Graph Neural Networks

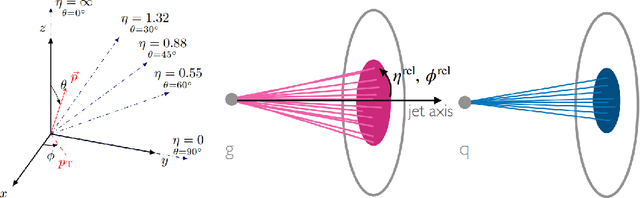
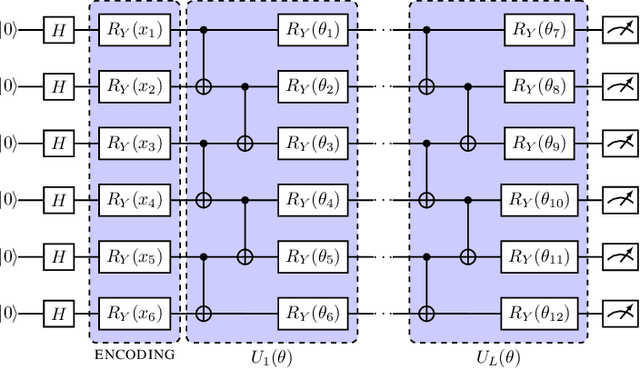
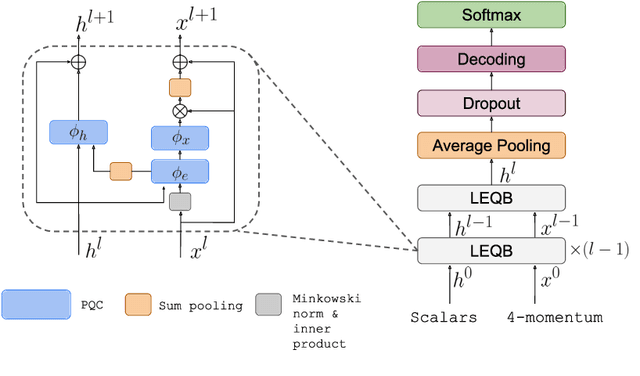
Discovering new phenomena at the Large Hadron Collider (LHC) involves the identification of rare signals over conventional backgrounds. Thus binary classification tasks are ubiquitous in analyses of the vast amounts of LHC data. We develop a Lie-Equivariant Quantum Graph Neural Network (Lie-EQGNN), a quantum model that is not only data efficient, but also has symmetry-preserving properties. Since Lorentz group equivariance has been shown to be beneficial for jet tagging, we build a Lorentz-equivariant quantum GNN for quark-gluon jet discrimination and show that its performance is on par with its classical state-of-the-art counterpart LorentzNet, making it a viable alternative to the conventional computing paradigm.

Quantum Attention for Vision Transformers in High Energy Physics

We present a novel hybrid quantum-classical vision transformer architecture incorporating quantum orthogonal neural networks (QONNs) to enhance performance and computational efficiency in high-energy physics applications. Building on advancements in quantum vision transformers, our approach addresses limitations of prior models by leveraging the inherent advantages of QONNs, including stability and efficient parameterization in high-dimensional spaces. We evaluate the proposed architecture using multi-detector jet images from CMS Open Data, focusing on the task of distinguishing quark-initiated from gluon-initiated jets. The results indicate that embedding quantum orthogonal transformations within the attention mechanism can provide robust performance while offering promising scalability for machine learning challenges associated with the upcoming High Luminosity Large Hadron Collider. This work highlights the potential of quantum-enhanced models to address the computational demands of next-generation particle physics experiments.

A Machine Learning Approach to Detecting Albedo Anomalies on the Lunar Surface

This study introduces a data-driven approach using machine learning (ML) techniques to explore and predict albedo anomalies on the Moon's surface. The research leverages diverse planetary datasets, including high-spatial-resolution albedo maps and element maps (LPFe, LPK, LPTh, LPTi) derived from laser and gamma-ray measurements. The primary objective is to identify relationships between chemical elements and albedo, thereby expanding our understanding of planetary surfaces and offering predictive capabilities for areas with incomplete datasets. To bridge the gap in resolution between the albedo and element maps, we employ Gaussian blurring techniques, including an innovative adaptive Gaussian blur. Our methodology culminates in the deployment of an Extreme Gradient Boosting Regression Model, optimized to predict full albedo based on elemental composition. Furthermore, we present an interactive analytical tool to visualize prediction errors, delineating their spatial and chemical characteristics. The findings not only pave the way for a more comprehensive understanding of the Moon's surface but also provide a framework for similar studies on other celestial bodies.

SineKAN: Kolmogorov-Arnold Networks Using Sinusoidal Activation Functions

Recent work has established an alternative to traditional multi-layer perceptron neural networks in the form of Kolmogorov-Arnold Networks (KAN). The general KAN framework uses learnable activation functions on the edges of the computational graph followed by summation on nodes. The learnable edge activation functions in the original implementation are basis spline functions (B-Spline). Here, we present a model in which learnable grids of B-Spline activation functions can be replaced by grids of re-weighted sine functions. We show that this leads to better or comparable numerical performance to B-Spline KAN models on the MNIST benchmark, while also providing a substantial speed increase on the order of 4-9 times.

Quantum Vision Transformers for Quark-Gluon Classification

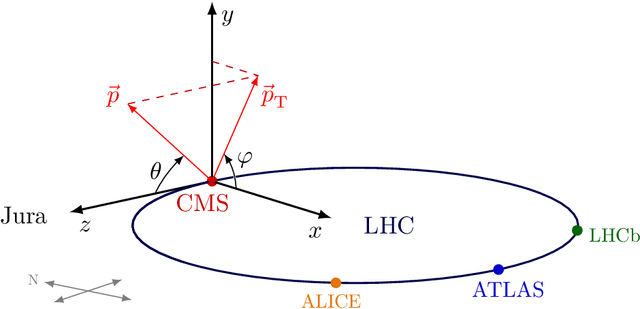
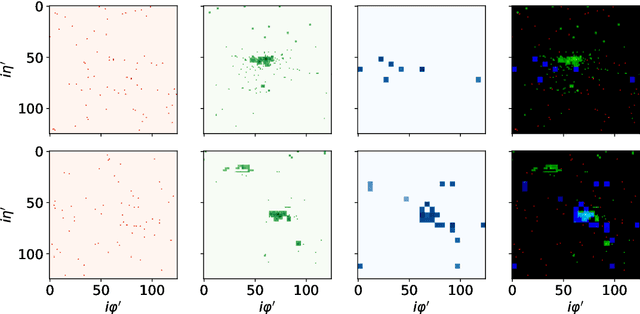
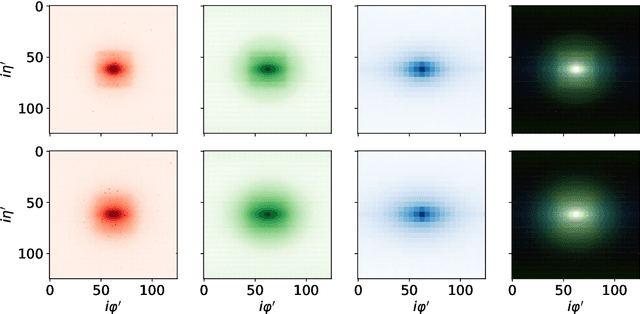
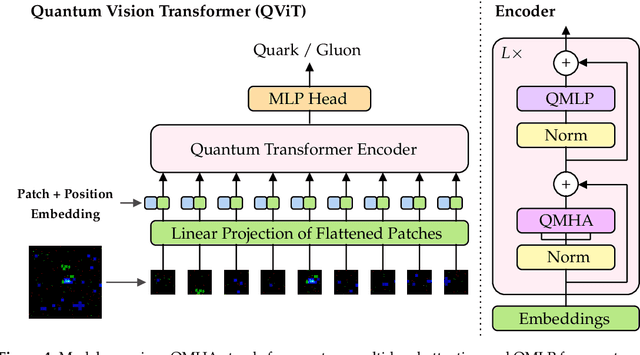
We introduce a hybrid quantum-classical vision transformer architecture, notable for its integration of variational quantum circuits within both the attention mechanism and the multi-layer perceptrons. The research addresses the critical challenge of computational efficiency and resource constraints in analyzing data from the upcoming High Luminosity Large Hadron Collider, presenting the architecture as a potential solution. In particular, we evaluate our method by applying the model to multi-detector jet images from CMS Open Data. The goal is to distinguish quark-initiated from gluon-initiated jets. We successfully train the quantum model and evaluate it via numerical simulations. Using this approach, we achieve classification performance almost on par with the one obtained with the completely classical architecture, considering a similar number of parameters.

Hybrid Quantum Vision Transformers for Event Classification in High Energy Physics

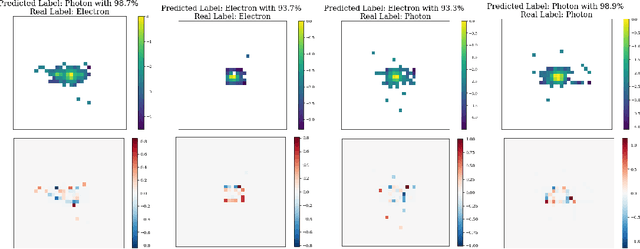
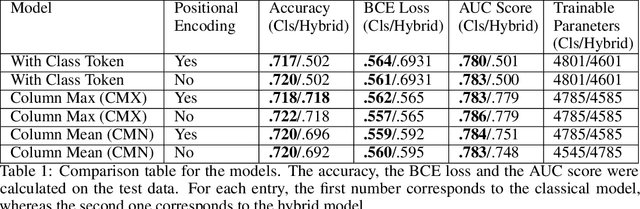
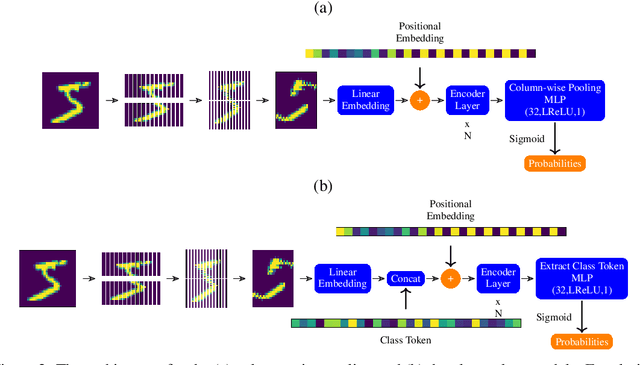
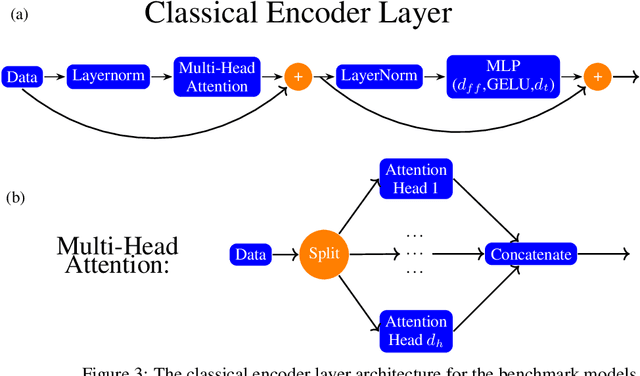
Models based on vision transformer architectures are considered state-of-the-art when it comes to image classification tasks. However, they require extensive computational resources both for training and deployment. The problem is exacerbated as the amount and complexity of the data increases. Quantum-based vision transformer models could potentially alleviate this issue by reducing the training and operating time while maintaining the same predictive power. Although current quantum computers are not yet able to perform high-dimensional tasks yet, they do offer one of the most efficient solutions for the future. In this work, we construct several variations of a quantum hybrid vision transformer for a classification problem in high energy physics (distinguishing photons and electrons in the electromagnetic calorimeter). We test them against classical vision transformer architectures. Our findings indicate that the hybrid models can achieve comparable performance to their classical analogues with a similar number of parameters.

$\mathbb{Z}_2\times \mathbb{Z}_2$ Equivariant Quantum Neural Networks: Benchmarking against Classical Neural Networks

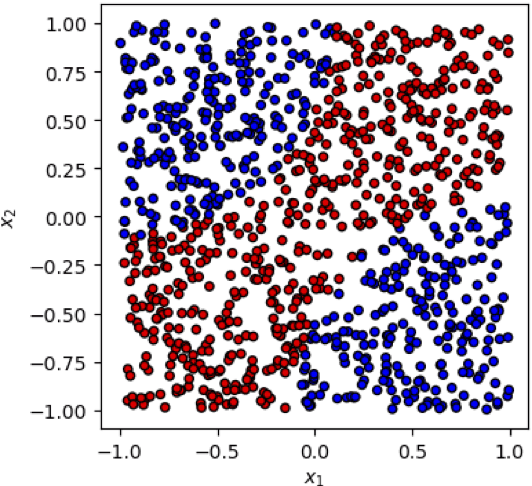
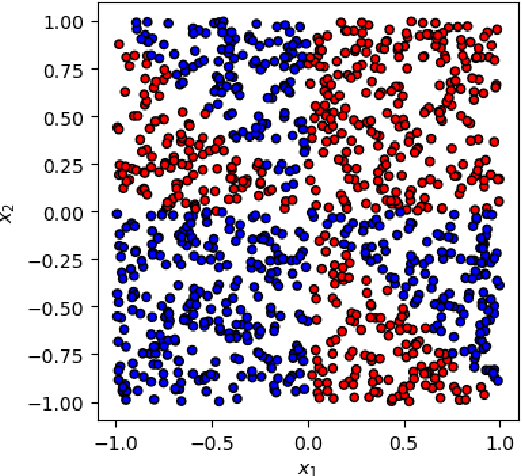
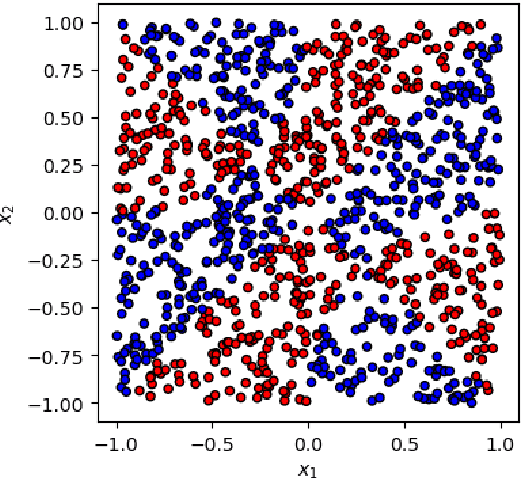
This paper presents a comprehensive comparative analysis of the performance of Equivariant Quantum Neural Networks (EQNN) and Quantum Neural Networks (QNN), juxtaposed against their classical counterparts: Equivariant Neural Networks (ENN) and Deep Neural Networks (DNN). We evaluate the performance of each network with two toy examples for a binary classification task, focusing on model complexity (measured by the number of parameters) and the size of the training data set. Our results show that the $\mathbb{Z}_2\times \mathbb{Z}_2$ EQNN and the QNN provide superior performance for smaller parameter sets and modest training data samples.