Kyoungchul Kong
Quantum Diffusion Model for Quark and Gluon Jet Generation
Dec 30, 2024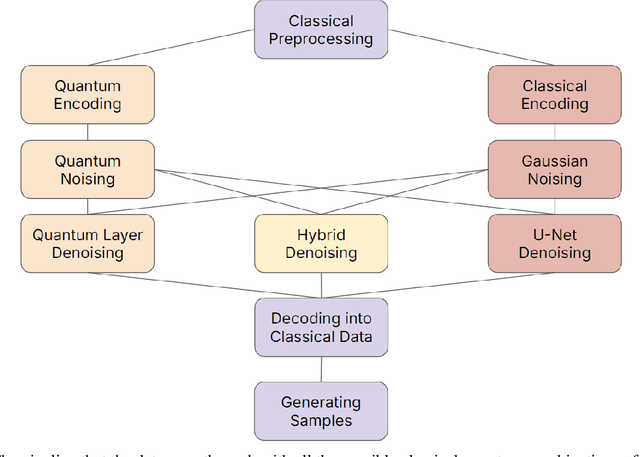

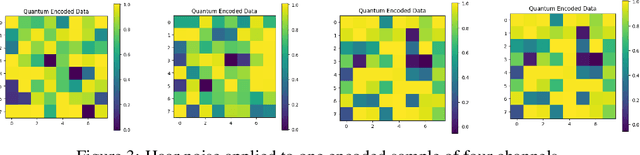
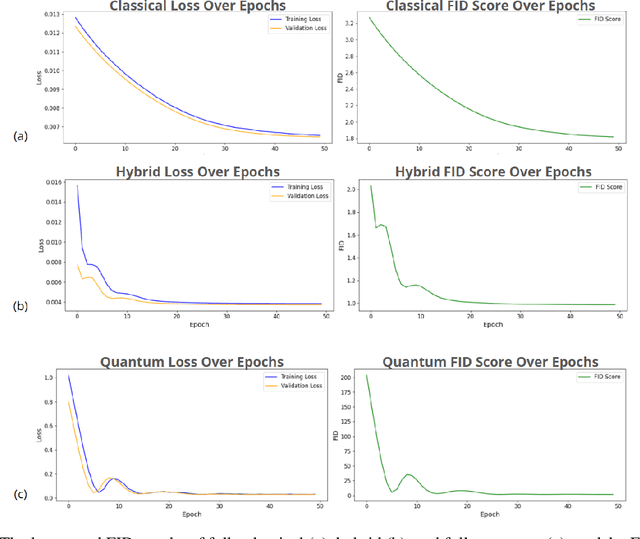
Abstract:Diffusion models have demonstrated remarkable success in image generation, but they are computationally intensive and time-consuming to train. In this paper, we introduce a novel diffusion model that benefits from quantum computing techniques in order to mitigate computational challenges and enhance generative performance within high energy physics data. The fully quantum diffusion model replaces Gaussian noise with random unitary matrices in the forward process and incorporates a variational quantum circuit within the U-Net in the denoising architecture. We run evaluations on the structurally complex quark and gluon jets dataset from the Large Hadron Collider. The results demonstrate that the fully quantum and hybrid models are competitive with a similar classical model for jet generation, highlighting the potential of using quantum techniques for machine learning problems.
Lie-Equivariant Quantum Graph Neural Networks
Nov 22, 2024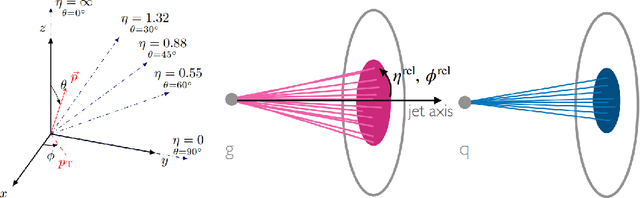

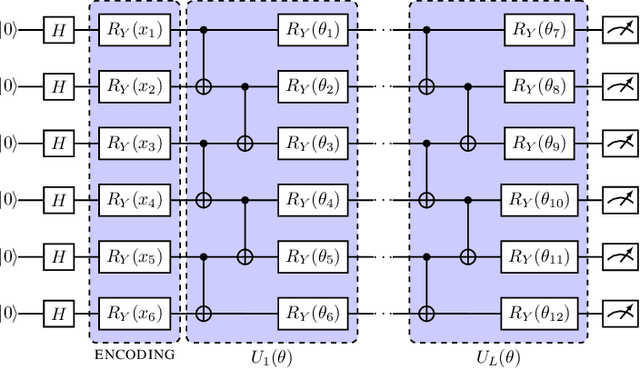
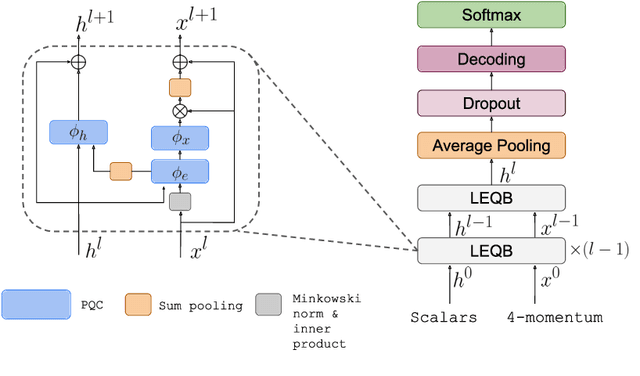
Abstract:Discovering new phenomena at the Large Hadron Collider (LHC) involves the identification of rare signals over conventional backgrounds. Thus binary classification tasks are ubiquitous in analyses of the vast amounts of LHC data. We develop a Lie-Equivariant Quantum Graph Neural Network (Lie-EQGNN), a quantum model that is not only data efficient, but also has symmetry-preserving properties. Since Lorentz group equivariance has been shown to be beneficial for jet tagging, we build a Lorentz-equivariant quantum GNN for quark-gluon jet discrimination and show that its performance is on par with its classical state-of-the-art counterpart LorentzNet, making it a viable alternative to the conventional computing paradigm.
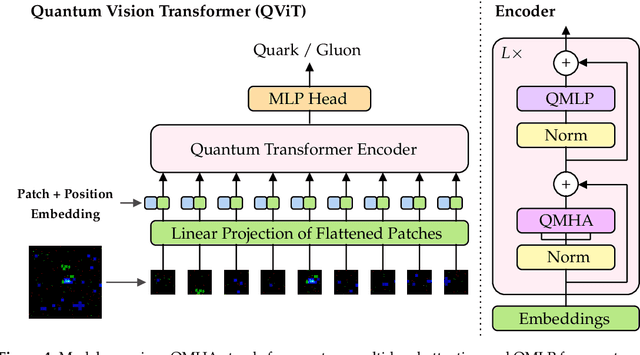
Quantum Attention for Vision Transformers in High Energy Physics
Nov 20, 2024Abstract:We present a novel hybrid quantum-classical vision transformer architecture incorporating quantum orthogonal neural networks (QONNs) to enhance performance and computational efficiency in high-energy physics applications. Building on advancements in quantum vision transformers, our approach addresses limitations of prior models by leveraging the inherent advantages of QONNs, including stability and efficient parameterization in high-dimensional spaces. We evaluate the proposed architecture using multi-detector jet images from CMS Open Data, focusing on the task of distinguishing quark-initiated from gluon-initiated jets. The results indicate that embedding quantum orthogonal transformations within the attention mechanism can provide robust performance while offering promising scalability for machine learning challenges associated with the upcoming High Luminosity Large Hadron Collider. This work highlights the potential of quantum-enhanced models to address the computational demands of next-generation particle physics experiments.
Quantum Vision Transformers for Quark-Gluon Classification
May 16, 2024
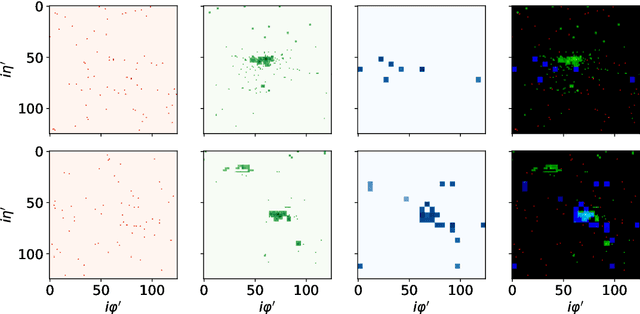
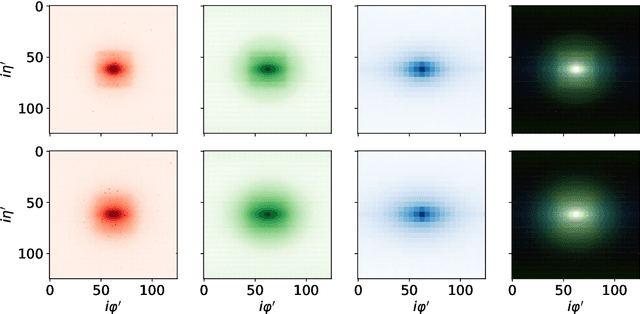
Abstract:We introduce a hybrid quantum-classical vision transformer architecture, notable for its integration of variational quantum circuits within both the attention mechanism and the multi-layer perceptrons. The research addresses the critical challenge of computational efficiency and resource constraints in analyzing data from the upcoming High Luminosity Large Hadron Collider, presenting the architecture as a potential solution. In particular, we evaluate our method by applying the model to multi-detector jet images from CMS Open Data. The goal is to distinguish quark-initiated from gluon-initiated jets. We successfully train the quantum model and evaluate it via numerical simulations. Using this approach, we achieve classification performance almost on par with the one obtained with the completely classical architecture, considering a similar number of parameters.
* 14 pages, 8 figures. Published in MDPI Axioms 2024, 13(5), 323
Hybrid Quantum Vision Transformers for Event Classification in High Energy Physics
Feb 01, 2024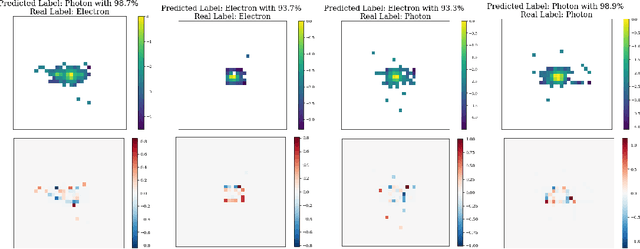
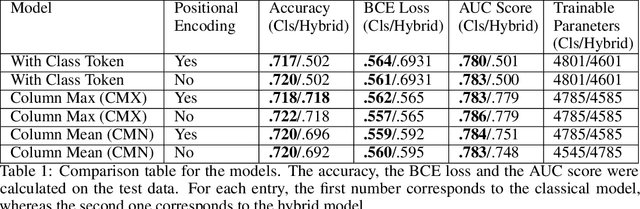
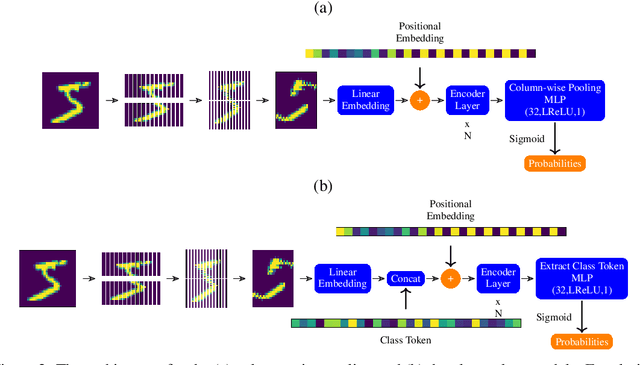
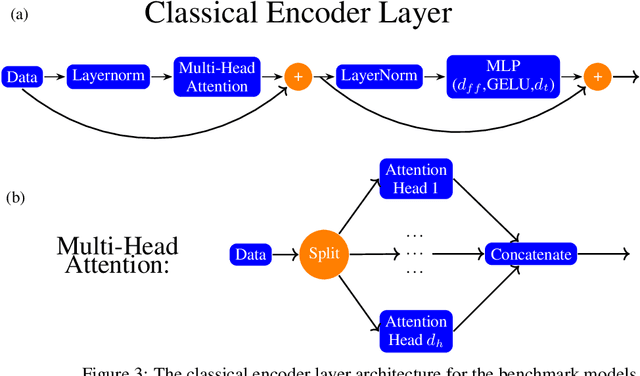
Abstract:Models based on vision transformer architectures are considered state-of-the-art when it comes to image classification tasks. However, they require extensive computational resources both for training and deployment. The problem is exacerbated as the amount and complexity of the data increases. Quantum-based vision transformer models could potentially alleviate this issue by reducing the training and operating time while maintaining the same predictive power. Although current quantum computers are not yet able to perform high-dimensional tasks yet, they do offer one of the most efficient solutions for the future. In this work, we construct several variations of a quantum hybrid vision transformer for a classification problem in high energy physics (distinguishing photons and electrons in the electromagnetic calorimeter). We test them against classical vision transformer architectures. Our findings indicate that the hybrid models can achieve comparable performance to their classical analogues with a similar number of parameters.
$\mathbb{Z}_2\times \mathbb{Z}_2$ Equivariant Quantum Neural Networks: Benchmarking against Classical Neural Networks
Nov 30, 2023
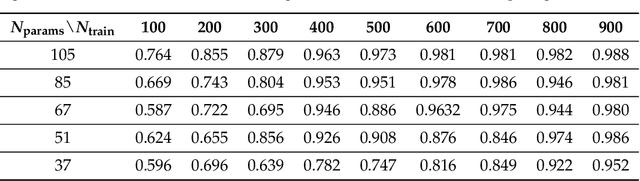
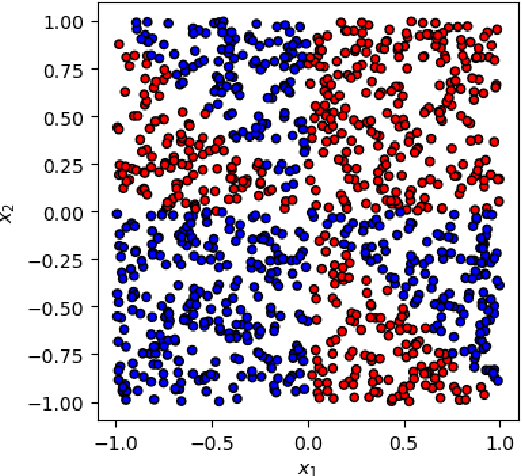
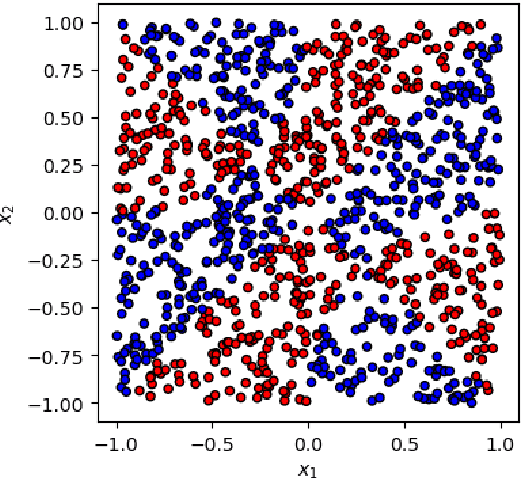
Abstract:This paper presents a comprehensive comparative analysis of the performance of Equivariant Quantum Neural Networks (EQNN) and Quantum Neural Networks (QNN), juxtaposed against their classical counterparts: Equivariant Neural Networks (ENN) and Deep Neural Networks (DNN). We evaluate the performance of each network with two toy examples for a binary classification task, focusing on model complexity (measured by the number of parameters) and the size of the training data set. Our results show that the $\mathbb{Z}_2\times \mathbb{Z}_2$ EQNN and the QNN provide superior performance for smaller parameter sets and modest training data samples.
A Comparison Between Invariant and Equivariant Classical and Quantum Graph Neural Networks
Nov 30, 2023



Abstract:Machine learning algorithms are heavily relied on to understand the vast amounts of data from high-energy particle collisions at the CERN Large Hadron Collider (LHC). The data from such collision events can naturally be represented with graph structures. Therefore, deep geometric methods, such as graph neural networks (GNNs), have been leveraged for various data analysis tasks in high-energy physics. One typical task is jet tagging, where jets are viewed as point clouds with distinct features and edge connections between their constituent particles. The increasing size and complexity of the LHC particle datasets, as well as the computational models used for their analysis, greatly motivate the development of alternative fast and efficient computational paradigms such as quantum computation. In addition, to enhance the validity and robustness of deep networks, one can leverage the fundamental symmetries present in the data through the use of invariant inputs and equivariant layers. In this paper, we perform a fair and comprehensive comparison between classical graph neural networks (GNNs) and equivariant graph neural networks (EGNNs) and their quantum counterparts: quantum graph neural networks (QGNNs) and equivariant quantum graph neural networks (EQGNN). The four architectures were benchmarked on a binary classification task to classify the parton-level particle initiating the jet. Based on their AUC scores, the quantum networks were shown to outperform the classical networks. However, seeing the computational advantage of the quantum networks in practice may have to wait for the further development of quantum technology and its associated APIs.
Is the Machine Smarter than the Theorist: Deriving Formulas for Particle Kinematics with Symbolic Regression
Nov 15, 2022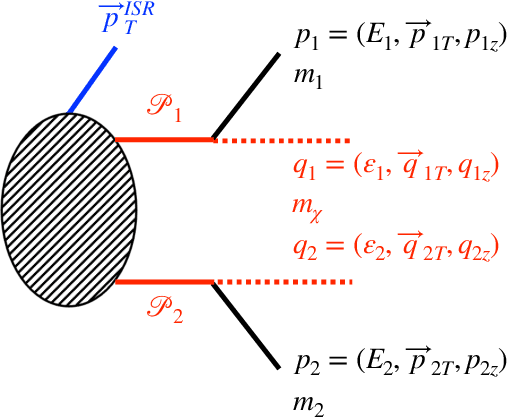
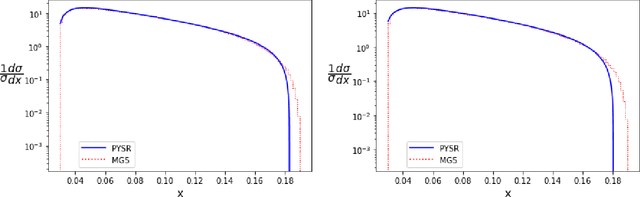
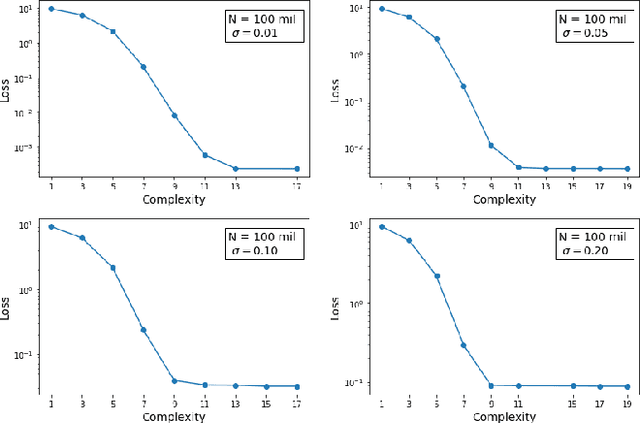
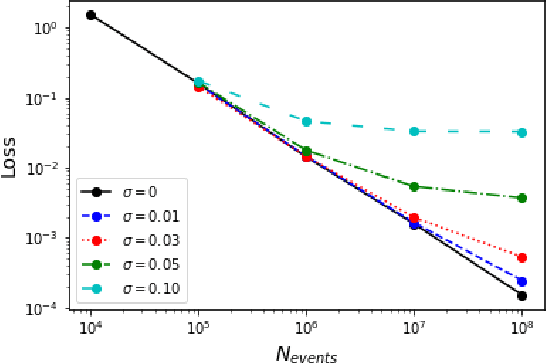
Abstract:We demonstrate the use of symbolic regression in deriving analytical formulas, which are needed at various stages of a typical experimental analysis in collider phenomenology. As a first application, we consider kinematic variables like the stransverse mass, $M_{T2}$, which are defined algorithmically through an optimization procedure and not in terms of an analytical formula. We then train a symbolic regression and obtain the correct analytical expressions for all known special cases of $M_{T2}$ in the literature. As a second application, we reproduce the correct analytical expression for a next-to-leading order (NLO) kinematic distribution from data, which is simulated with a NLO event generator. Finally, we derive analytical approximations for the NLO kinematic distributions after detector simulation, for which no known analytical formulas currently exist.
New Machine Learning Techniques for Simulation-Based Inference: InferoStatic Nets, Kernel Score Estimation, and Kernel Likelihood Ratio Estimation
Oct 04, 2022Abstract:We propose an intuitive, machine-learning approach to multiparameter inference, dubbed the InferoStatic Networks (ISN) method, to model the score and likelihood ratio estimators in cases when the probability density can be sampled but not computed directly. The ISN uses a backend neural network that models a scalar function called the inferostatic potential $\varphi$. In addition, we introduce new strategies, respectively called Kernel Score Estimation (KSE) and Kernel Likelihood Ratio Estimation (KLRE), to learn the score and the likelihood ratio functions from simulated data. We illustrate the new techniques with some toy examples and compare to existing approaches in the literature. We mention en passant some new loss functions that optimally incorporate latent information from simulations into the training procedure.
Deep-Learned Event Variables for Collider Phenomenology
May 21, 2021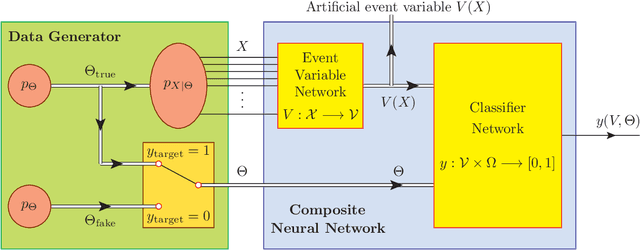

Abstract:The choice of optimal event variables is crucial for achieving the maximal sensitivity of experimental analyses. Over time, physicists have derived suitable kinematic variables for many typical event topologies in collider physics. Here we introduce a deep learning technique to design good event variables, which are sensitive over a wide range of values for the unknown model parameters. We demonstrate that the neural networks trained with our technique on some simple event topologies are able to reproduce standard event variables like invariant mass, transverse mass, and stransverse mass. The method is automatable, completely general, and can be used to derive sensitive, previously unknown, event variables for other, more complex event topologies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge