Marçal Comajoan Cara
Quantum Vision Transformers for Quark-Gluon Classification
May 16, 2024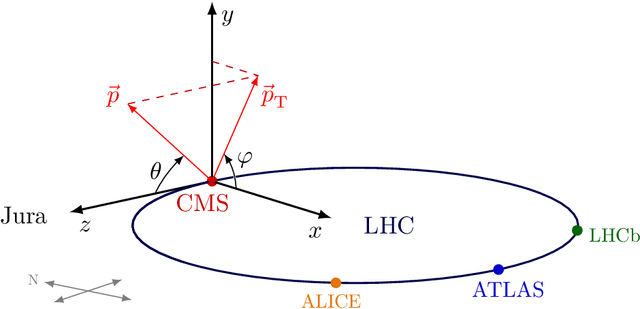
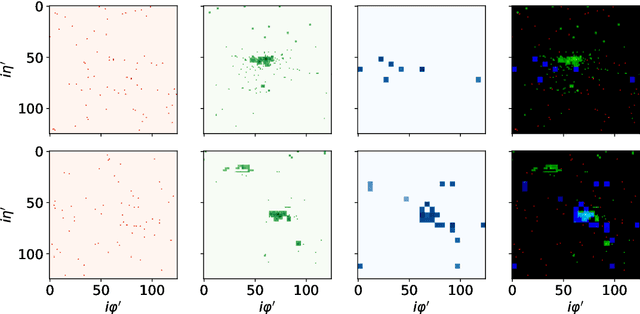
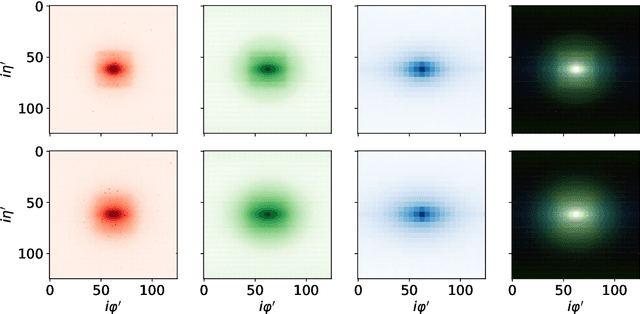
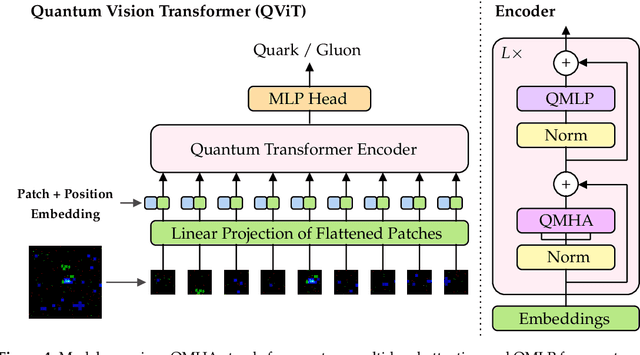
Abstract:We introduce a hybrid quantum-classical vision transformer architecture, notable for its integration of variational quantum circuits within both the attention mechanism and the multi-layer perceptrons. The research addresses the critical challenge of computational efficiency and resource constraints in analyzing data from the upcoming High Luminosity Large Hadron Collider, presenting the architecture as a potential solution. In particular, we evaluate our method by applying the model to multi-detector jet images from CMS Open Data. The goal is to distinguish quark-initiated from gluon-initiated jets. We successfully train the quantum model and evaluate it via numerical simulations. Using this approach, we achieve classification performance almost on par with the one obtained with the completely classical architecture, considering a similar number of parameters.
* 14 pages, 8 figures. Published in MDPI Axioms 2024, 13(5), 323
Hybrid Quantum Vision Transformers for Event Classification in High Energy Physics
Feb 01, 2024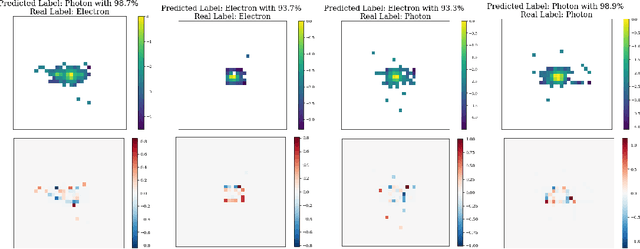
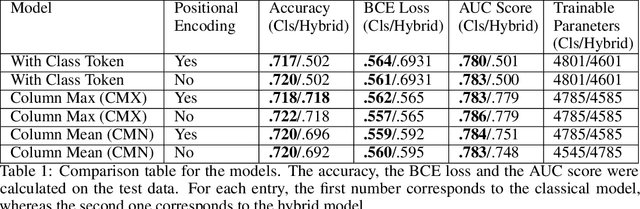
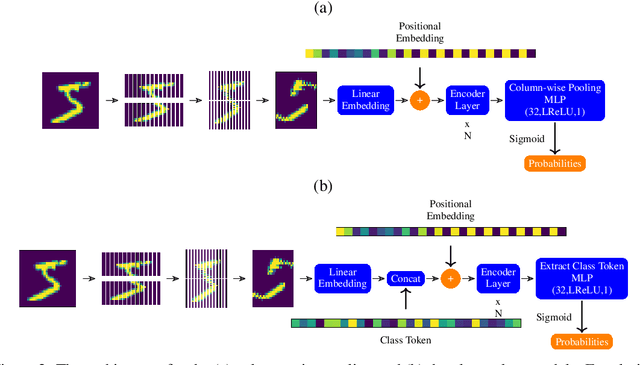
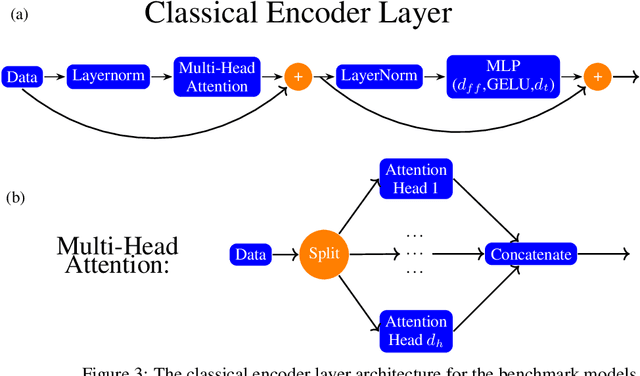
Abstract:Models based on vision transformer architectures are considered state-of-the-art when it comes to image classification tasks. However, they require extensive computational resources both for training and deployment. The problem is exacerbated as the amount and complexity of the data increases. Quantum-based vision transformer models could potentially alleviate this issue by reducing the training and operating time while maintaining the same predictive power. Although current quantum computers are not yet able to perform high-dimensional tasks yet, they do offer one of the most efficient solutions for the future. In this work, we construct several variations of a quantum hybrid vision transformer for a classification problem in high energy physics (distinguishing photons and electrons in the electromagnetic calorimeter). We test them against classical vision transformer architectures. Our findings indicate that the hybrid models can achieve comparable performance to their classical analogues with a similar number of parameters.
$\mathbb{Z}_2\times \mathbb{Z}_2$ Equivariant Quantum Neural Networks: Benchmarking against Classical Neural Networks
Nov 30, 2023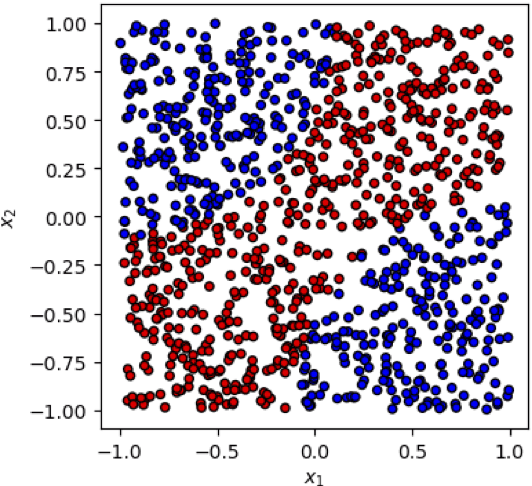
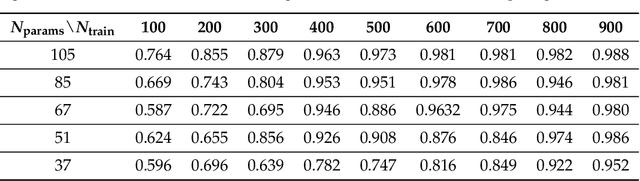
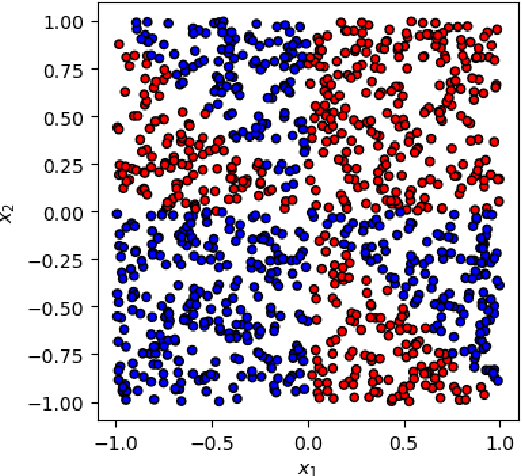
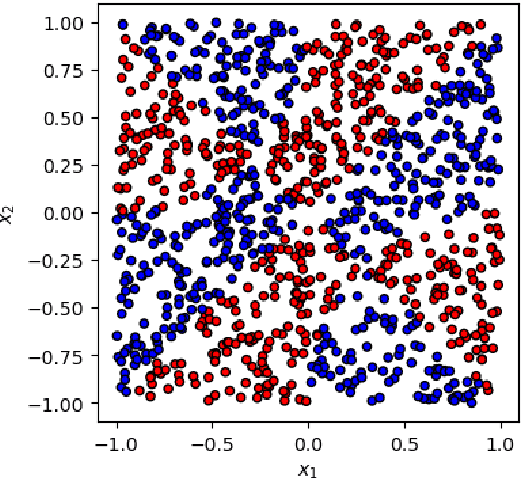
Abstract:This paper presents a comprehensive comparative analysis of the performance of Equivariant Quantum Neural Networks (EQNN) and Quantum Neural Networks (QNN), juxtaposed against their classical counterparts: Equivariant Neural Networks (ENN) and Deep Neural Networks (DNN). We evaluate the performance of each network with two toy examples for a binary classification task, focusing on model complexity (measured by the number of parameters) and the size of the training data set. Our results show that the $\mathbb{Z}_2\times \mathbb{Z}_2$ EQNN and the QNN provide superior performance for smaller parameter sets and modest training data samples.
A Comparison Between Invariant and Equivariant Classical and Quantum Graph Neural Networks
Nov 30, 2023



Abstract:Machine learning algorithms are heavily relied on to understand the vast amounts of data from high-energy particle collisions at the CERN Large Hadron Collider (LHC). The data from such collision events can naturally be represented with graph structures. Therefore, deep geometric methods, such as graph neural networks (GNNs), have been leveraged for various data analysis tasks in high-energy physics. One typical task is jet tagging, where jets are viewed as point clouds with distinct features and edge connections between their constituent particles. The increasing size and complexity of the LHC particle datasets, as well as the computational models used for their analysis, greatly motivate the development of alternative fast and efficient computational paradigms such as quantum computation. In addition, to enhance the validity and robustness of deep networks, one can leverage the fundamental symmetries present in the data through the use of invariant inputs and equivariant layers. In this paper, we perform a fair and comprehensive comparison between classical graph neural networks (GNNs) and equivariant graph neural networks (EGNNs) and their quantum counterparts: quantum graph neural networks (QGNNs) and equivariant quantum graph neural networks (EQGNN). The four architectures were benchmarked on a binary classification task to classify the parton-level particle initiating the jet. Based on their AUC scores, the quantum networks were shown to outperform the classical networks. However, seeing the computational advantage of the quantum networks in practice may have to wait for the further development of quantum technology and its associated APIs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge