Roy T. Forestano
Lie-Equivariant Quantum Graph Neural Networks
Nov 22, 2024Abstract:Discovering new phenomena at the Large Hadron Collider (LHC) involves the identification of rare signals over conventional backgrounds. Thus binary classification tasks are ubiquitous in analyses of the vast amounts of LHC data. We develop a Lie-Equivariant Quantum Graph Neural Network (Lie-EQGNN), a quantum model that is not only data efficient, but also has symmetry-preserving properties. Since Lorentz group equivariance has been shown to be beneficial for jet tagging, we build a Lorentz-equivariant quantum GNN for quark-gluon jet discrimination and show that its performance is on par with its classical state-of-the-art counterpart LorentzNet, making it a viable alternative to the conventional computing paradigm.
Quantum Vision Transformers for Quark-Gluon Classification
May 16, 2024Abstract:We introduce a hybrid quantum-classical vision transformer architecture, notable for its integration of variational quantum circuits within both the attention mechanism and the multi-layer perceptrons. The research addresses the critical challenge of computational efficiency and resource constraints in analyzing data from the upcoming High Luminosity Large Hadron Collider, presenting the architecture as a potential solution. In particular, we evaluate our method by applying the model to multi-detector jet images from CMS Open Data. The goal is to distinguish quark-initiated from gluon-initiated jets. We successfully train the quantum model and evaluate it via numerical simulations. Using this approach, we achieve classification performance almost on par with the one obtained with the completely classical architecture, considering a similar number of parameters.
* 14 pages, 8 figures. Published in MDPI Axioms 2024, 13(5), 323
Hybrid Quantum Vision Transformers for Event Classification in High Energy Physics
Feb 01, 2024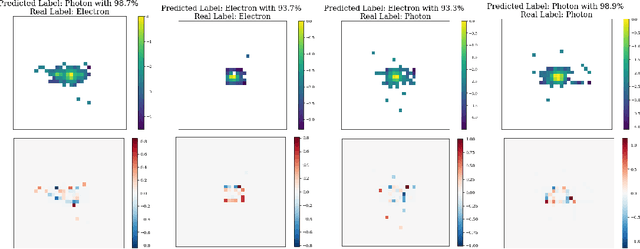
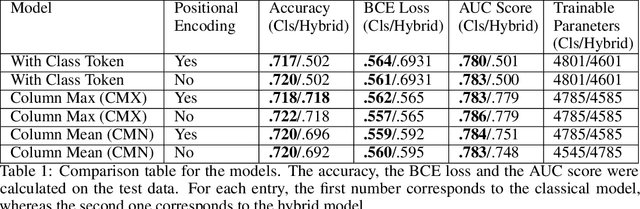
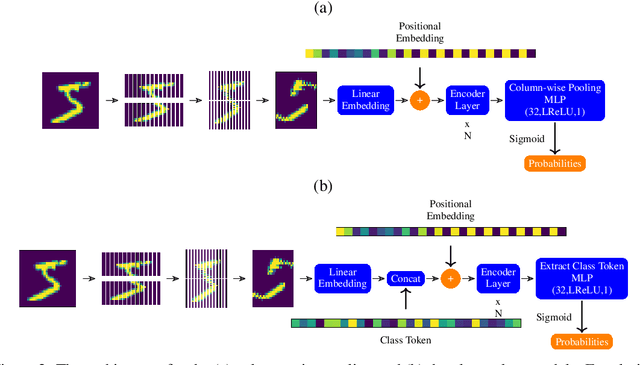
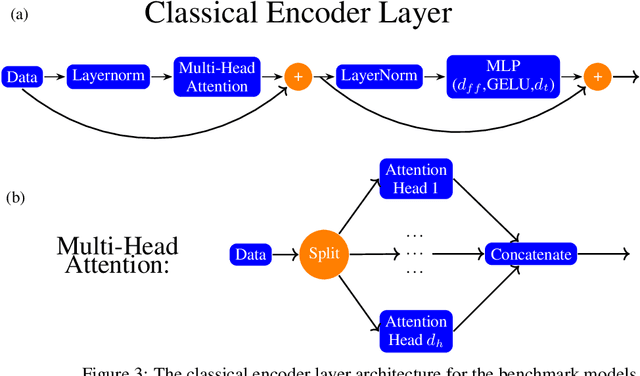
Abstract:Models based on vision transformer architectures are considered state-of-the-art when it comes to image classification tasks. However, they require extensive computational resources both for training and deployment. The problem is exacerbated as the amount and complexity of the data increases. Quantum-based vision transformer models could potentially alleviate this issue by reducing the training and operating time while maintaining the same predictive power. Although current quantum computers are not yet able to perform high-dimensional tasks yet, they do offer one of the most efficient solutions for the future. In this work, we construct several variations of a quantum hybrid vision transformer for a classification problem in high energy physics (distinguishing photons and electrons in the electromagnetic calorimeter). We test them against classical vision transformer architectures. Our findings indicate that the hybrid models can achieve comparable performance to their classical analogues with a similar number of parameters.
A Comparison Between Invariant and Equivariant Classical and Quantum Graph Neural Networks
Nov 30, 2023



Abstract:Machine learning algorithms are heavily relied on to understand the vast amounts of data from high-energy particle collisions at the CERN Large Hadron Collider (LHC). The data from such collision events can naturally be represented with graph structures. Therefore, deep geometric methods, such as graph neural networks (GNNs), have been leveraged for various data analysis tasks in high-energy physics. One typical task is jet tagging, where jets are viewed as point clouds with distinct features and edge connections between their constituent particles. The increasing size and complexity of the LHC particle datasets, as well as the computational models used for their analysis, greatly motivate the development of alternative fast and efficient computational paradigms such as quantum computation. In addition, to enhance the validity and robustness of deep networks, one can leverage the fundamental symmetries present in the data through the use of invariant inputs and equivariant layers. In this paper, we perform a fair and comprehensive comparison between classical graph neural networks (GNNs) and equivariant graph neural networks (EGNNs) and their quantum counterparts: quantum graph neural networks (QGNNs) and equivariant quantum graph neural networks (EQGNN). The four architectures were benchmarked on a binary classification task to classify the parton-level particle initiating the jet. Based on their AUC scores, the quantum networks were shown to outperform the classical networks. However, seeing the computational advantage of the quantum networks in practice may have to wait for the further development of quantum technology and its associated APIs.
$\mathbb{Z}_2\times \mathbb{Z}_2$ Equivariant Quantum Neural Networks: Benchmarking against Classical Neural Networks
Nov 30, 2023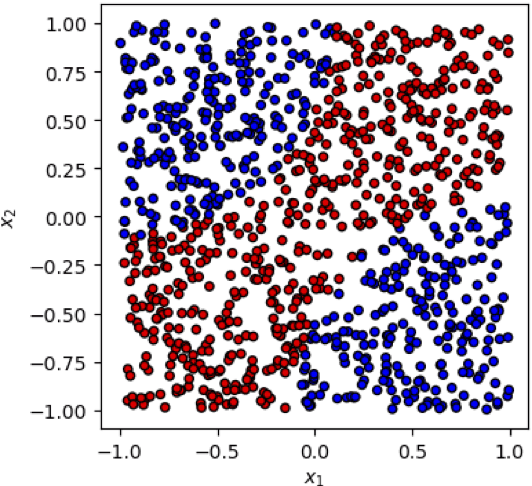
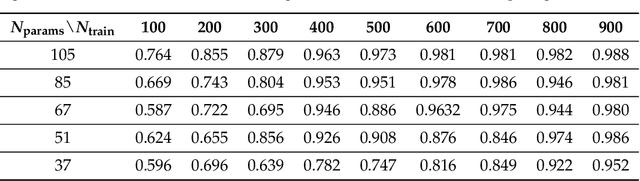
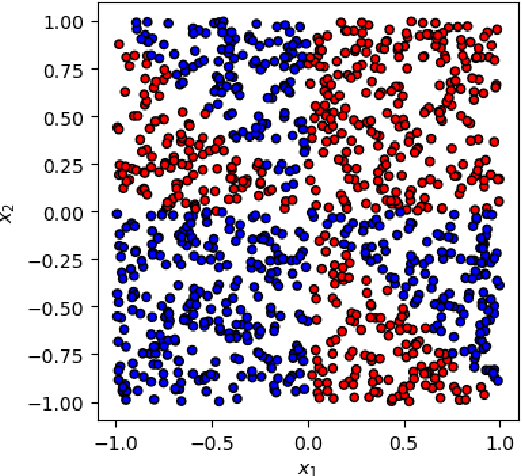
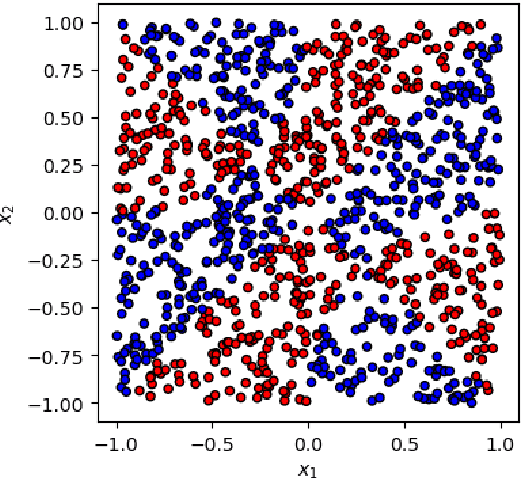
Abstract:This paper presents a comprehensive comparative analysis of the performance of Equivariant Quantum Neural Networks (EQNN) and Quantum Neural Networks (QNN), juxtaposed against their classical counterparts: Equivariant Neural Networks (ENN) and Deep Neural Networks (DNN). We evaluate the performance of each network with two toy examples for a binary classification task, focusing on model complexity (measured by the number of parameters) and the size of the training data set. Our results show that the $\mathbb{Z}_2\times \mathbb{Z}_2$ EQNN and the QNN provide superior performance for smaller parameter sets and modest training data samples.
Reproducing Bayesian Posterior Distributions for Exoplanet Atmospheric Parameter Retrievals with a Machine Learning Surrogate Model
Oct 16, 2023Abstract:We describe a machine-learning-based surrogate model for reproducing the Bayesian posterior distributions for exoplanet atmospheric parameters derived from transmission spectra of transiting planets with typical retrieval software such as TauRex. The model is trained on ground truth distributions for seven parameters: the planet radius, the atmospheric temperature, and the mixing ratios for five common absorbers: $H_2O$, $CH_4$, $NH_3$, $CO$ and $CO_2$. The model performance is enhanced by domain-inspired preprocessing of the features and the use of semi-supervised learning in order to leverage the large amount of unlabelled training data available. The model was among the winning solutions in the 2023 Ariel Machine Learning Data Challenge.
Identifying the Group-Theoretic Structure of Machine-Learned Symmetries
Sep 14, 2023Abstract:Deep learning was recently successfully used in deriving symmetry transformations that preserve important physics quantities. Being completely agnostic, these techniques postpone the identification of the discovered symmetries to a later stage. In this letter we propose methods for examining and identifying the group-theoretic structure of such machine-learned symmetries. We design loss functions which probe the subalgebra structure either during the deep learning stage of symmetry discovery or in a subsequent post-processing stage. We illustrate the new methods with examples from the U(n) Lie group family, obtaining the respective subalgebra decompositions. As an application to particle physics, we demonstrate the identification of the residual symmetries after the spontaneous breaking of non-Abelian gauge symmetries like SU(3) and SU(5) which are commonly used in model building.
Searching for Novel Chemistry in Exoplanetary Atmospheres using Machine Learning for Anomaly Detection
Aug 15, 2023Abstract:The next generation of telescopes will yield a substantial increase in the availability of high-resolution spectroscopic data for thousands of exoplanets. The sheer volume of data and number of planets to be analyzed greatly motivate the development of new, fast and efficient methods for flagging interesting planets for reobservation and detailed analysis. We advocate the application of machine learning (ML) techniques for anomaly (novelty) detection to exoplanet transit spectra, with the goal of identifying planets with unusual chemical composition and even searching for unknown biosignatures. We successfully demonstrate the feasibility of two popular anomaly detection methods (Local Outlier Factor and One Class Support Vector Machine) on a large public database of synthetic spectra. We consider several test cases, each with different levels of instrumental noise. In each case, we use ROC curves to quantify and compare the performance of the two ML techniques.
Accelerated Discovery of Machine-Learned Symmetries: Deriving the Exceptional Lie Groups G2, F4 and E6
Jul 10, 2023Abstract:Recent work has applied supervised deep learning to derive continuous symmetry transformations that preserve the data labels and to obtain the corresponding algebras of symmetry generators. This letter introduces two improved algorithms that significantly speed up the discovery of these symmetry transformations. The new methods are demonstrated by deriving the complete set of generators for the unitary groups U(n) and the exceptional Lie groups $G_2$, $F_4$, and $E_6$. A third post-processing algorithm renders the found generators in sparse form. We benchmark the performance improvement of the new algorithms relative to the standard approach. Given the significant complexity of the exceptional Lie groups, our results demonstrate that this machine-learning method for discovering symmetries is completely general and can be applied to a wide variety of labeled datasets.
Discovering Sparse Representations of Lie Groups with Machine Learning
Feb 10, 2023Abstract:Recent work has used deep learning to derive symmetry transformations, which preserve conserved quantities, and to obtain the corresponding algebras of generators. In this letter, we extend this technique to derive sparse representations of arbitrary Lie algebras. We show that our method reproduces the canonical (sparse) representations of the generators of the Lorentz group, as well as the $U(n)$ and $SU(n)$ families of Lie groups. This approach is completely general and can be used to find the infinitesimal generators for any Lie group.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge