Towards shutdownable agents via stochastic choice

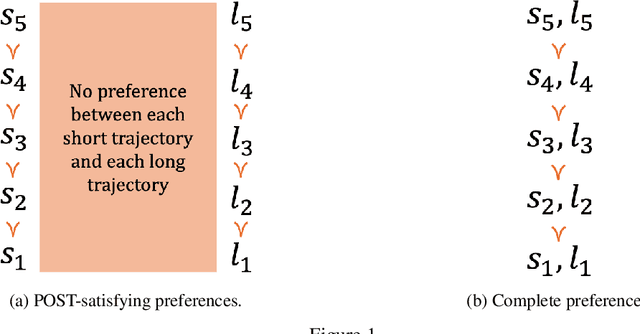
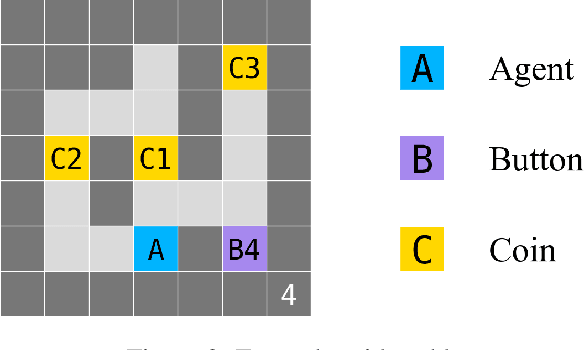
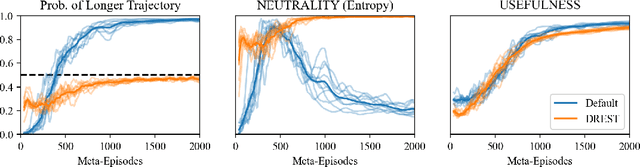
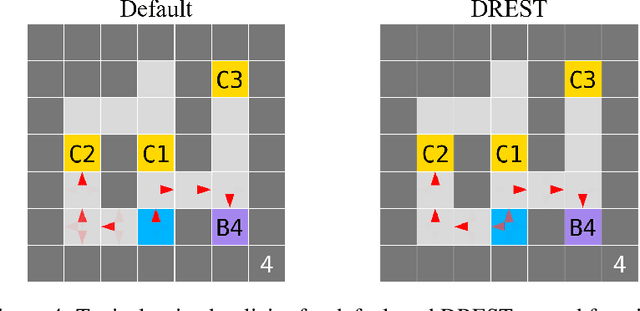
Some worry that advanced artificial agents may resist being shut down. The Incomplete Preferences Proposal (IPP) is an idea for ensuring that doesn't happen. A key part of the IPP is using a novel 'Discounted REward for Same-Length Trajectories (DREST)' reward function to train agents to (1) pursue goals effectively conditional on each trajectory-length (be 'USEFUL'), and (2) choose stochastically between different trajectory-lengths (be 'NEUTRAL' about trajectory-lengths). In this paper, we propose evaluation metrics for USEFULNESS and NEUTRALITY. We use a DREST reward function to train simple agents to navigate gridworlds, and we find that these agents learn to be USEFUL and NEUTRAL. Our results thus suggest that DREST reward functions could also train advanced agents to be USEFUL and NEUTRAL, and thereby make these advanced agents useful and shutdownable.

Identifying the Group-Theoretic Structure of Machine-Learned Symmetries

Deep learning was recently successfully used in deriving symmetry transformations that preserve important physics quantities. Being completely agnostic, these techniques postpone the identification of the discovered symmetries to a later stage. In this letter we propose methods for examining and identifying the group-theoretic structure of such machine-learned symmetries. We design loss functions which probe the subalgebra structure either during the deep learning stage of symmetry discovery or in a subsequent post-processing stage. We illustrate the new methods with examples from the U(n) Lie group family, obtaining the respective subalgebra decompositions. As an application to particle physics, we demonstrate the identification of the residual symmetries after the spontaneous breaking of non-Abelian gauge symmetries like SU(3) and SU(5) which are commonly used in model building.

Accelerated Discovery of Machine-Learned Symmetries: Deriving the Exceptional Lie Groups G2, F4 and E6

Recent work has applied supervised deep learning to derive continuous symmetry transformations that preserve the data labels and to obtain the corresponding algebras of symmetry generators. This letter introduces two improved algorithms that significantly speed up the discovery of these symmetry transformations. The new methods are demonstrated by deriving the complete set of generators for the unitary groups U(n) and the exceptional Lie groups $G_2$, $F_4$, and $E_6$. A third post-processing algorithm renders the found generators in sparse form. We benchmark the performance improvement of the new algorithms relative to the standard approach. Given the significant complexity of the exceptional Lie groups, our results demonstrate that this machine-learning method for discovering symmetries is completely general and can be applied to a wide variety of labeled datasets.

Discovering Sparse Representations of Lie Groups with Machine Learning

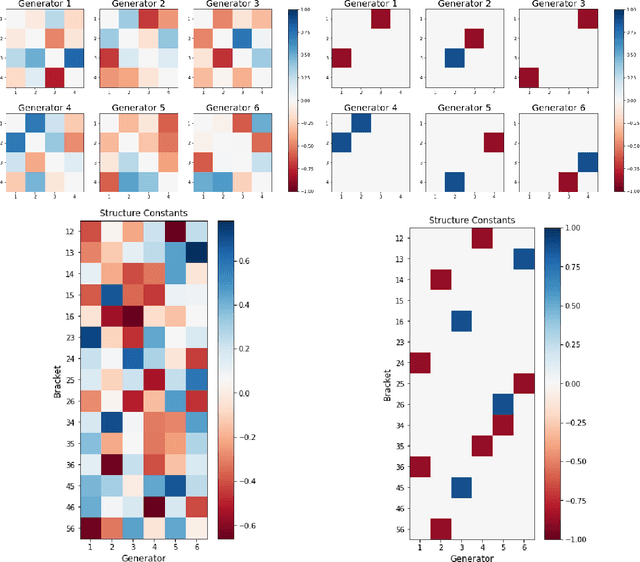
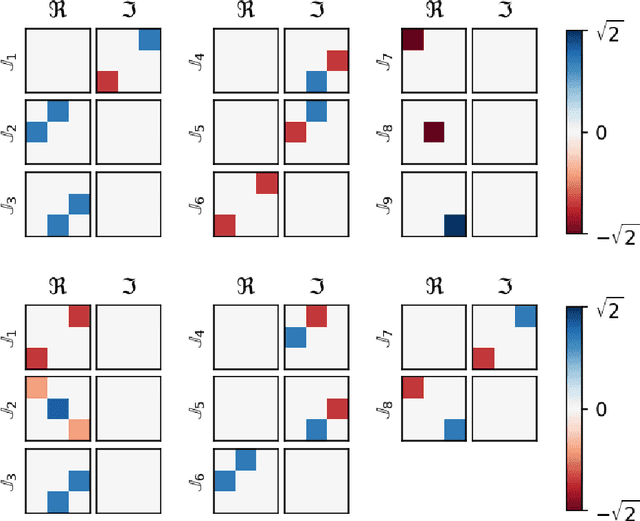
Recent work has used deep learning to derive symmetry transformations, which preserve conserved quantities, and to obtain the corresponding algebras of generators. In this letter, we extend this technique to derive sparse representations of arbitrary Lie algebras. We show that our method reproduces the canonical (sparse) representations of the generators of the Lorentz group, as well as the $U(n)$ and $SU(n)$ families of Lie groups. This approach is completely general and can be used to find the infinitesimal generators for any Lie group.

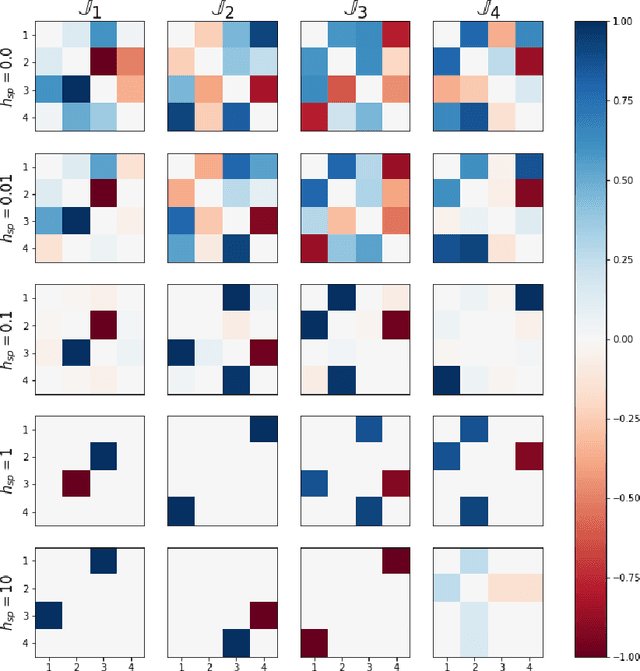
Oracle-Preserving Latent Flows

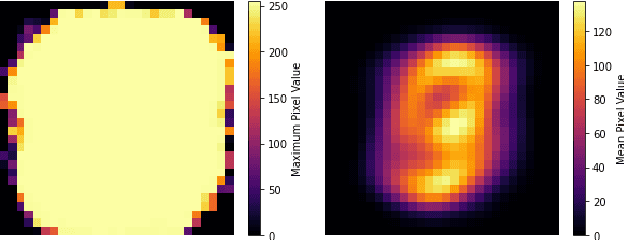
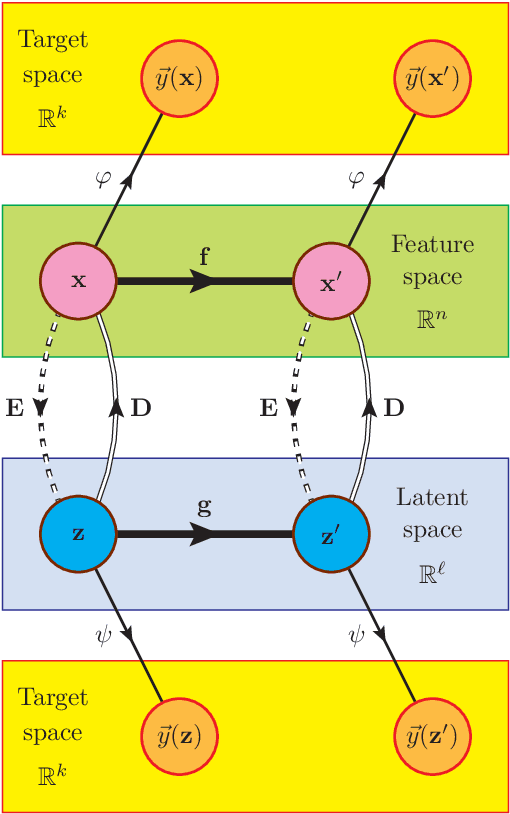
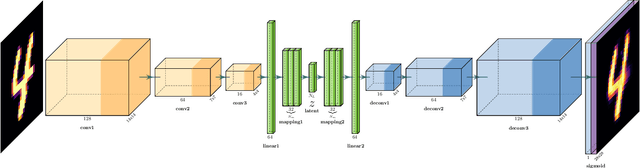
We develop a deep learning methodology for the simultaneous discovery of multiple nontrivial continuous symmetries across an entire labelled dataset. The symmetry transformations and the corresponding generators are modeled with fully connected neural networks trained with a specially constructed loss function ensuring the desired symmetry properties. The two new elements in this work are the use of a reduced-dimensionality latent space and the generalization to transformations invariant with respect to high-dimensional oracles. The method is demonstrated with several examples on the MNIST digit dataset.

Deep Learning Symmetries and Their Lie Groups, Algebras, and Subalgebras from First Principles

We design a deep-learning algorithm for the discovery and identification of the continuous group of symmetries present in a labeled dataset. We use fully connected neural networks to model the symmetry transformations and the corresponding generators. We construct loss functions that ensure that the applied transformations are symmetries and that the corresponding set of generators forms a closed (sub)algebra. Our procedure is validated with several examples illustrating different types of conserved quantities preserved by symmetry. In the process of deriving the full set of symmetries, we analyze the complete subgroup structure of the rotation groups $SO(2)$, $SO(3)$, and $SO(4)$, and of the Lorentz group $SO(1,3)$. Other examples include squeeze mapping, piecewise discontinuous labels, and $SO(10)$, demonstrating that our method is completely general, with many possible applications in physics and data science. Our study also opens the door for using a machine learning approach in the mathematical study of Lie groups and their properties.

Unsupervised Machine Learning for Exploratory Data Analysis of Exoplanet Transmission Spectra

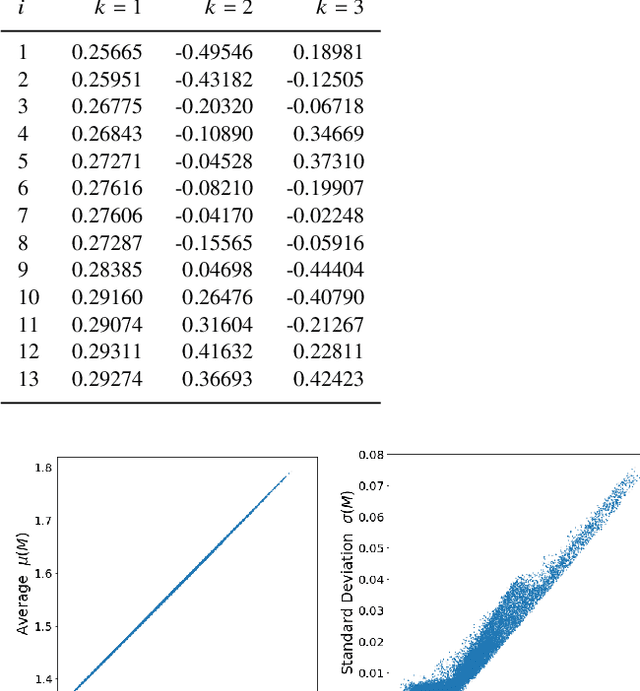
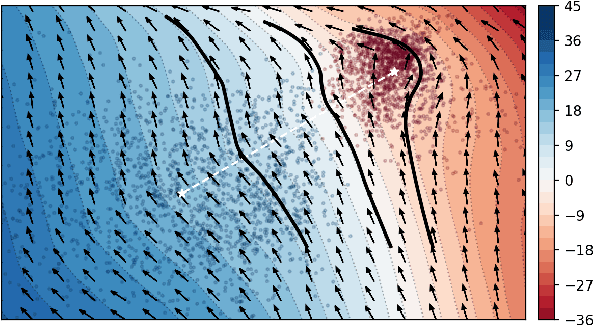
Transit spectroscopy is a powerful tool to decode the chemical composition of the atmospheres of extrasolar planets. In this paper we focus on unsupervised techniques for analyzing spectral data from transiting exoplanets. We demonstrate methods for i) cleaning and validating the data, ii) initial exploratory data analysis based on summary statistics (estimates of location and variability), iii) exploring and quantifying the existing correlations in the data, iv) pre-processing and linearly transforming the data to its principal components, v) dimensionality reduction and manifold learning, vi) clustering and anomaly detection, vii) visualization and interpretation of the data. To illustrate the proposed unsupervised methodology, we use a well-known public benchmark data set of synthetic transit spectra. We show that there is a high degree of correlation in the spectral data, which calls for appropriate low-dimensional representations. We explore a number of different techniques for such dimensionality reduction and identify several suitable options in terms of summary statistics, principal components, etc. We uncover interesting structures in the principal component basis, namely, well-defined branches corresponding to different chemical regimes of the underlying atmospheres. We demonstrate that those branches can be successfully recovered with a K-means clustering algorithm in fully unsupervised fashion. We advocate for a three-dimensional representation of the spectroscopic data in terms of the first three principal components, in order to reveal the existing structure in the data and quickly characterize the chemical class of a planet.

Analytical Modelling of Exoplanet Transit Specroscopy with Dimensional Analysis and Symbolic Regression

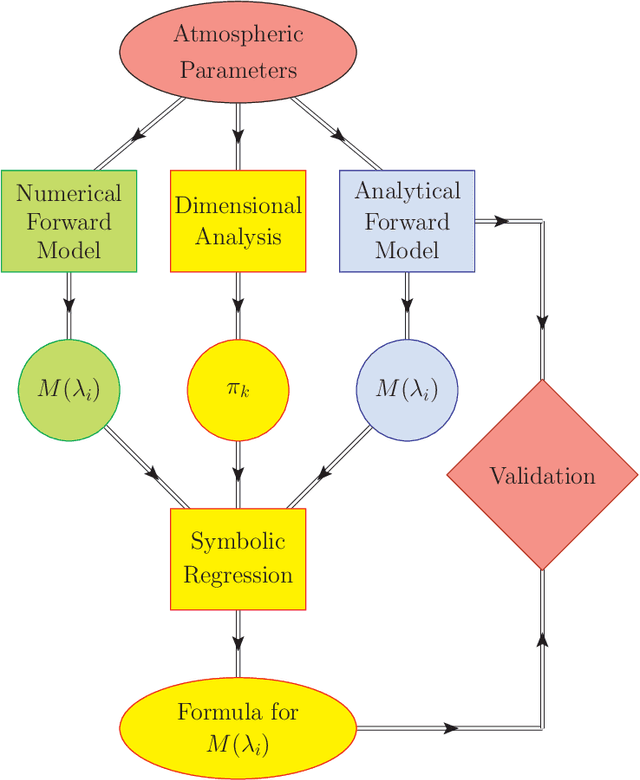
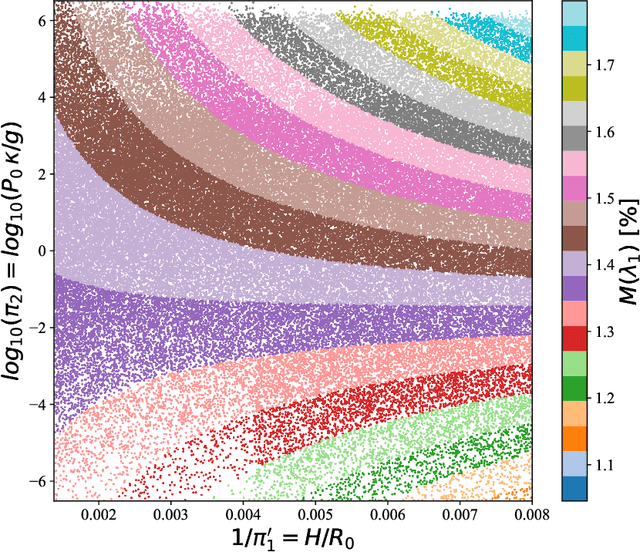
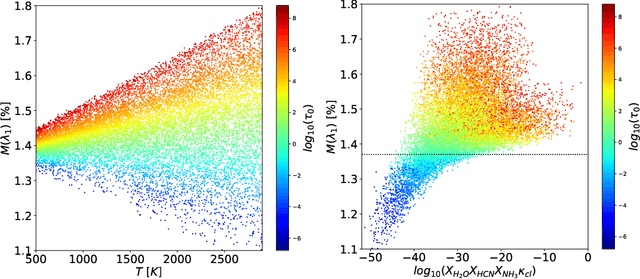
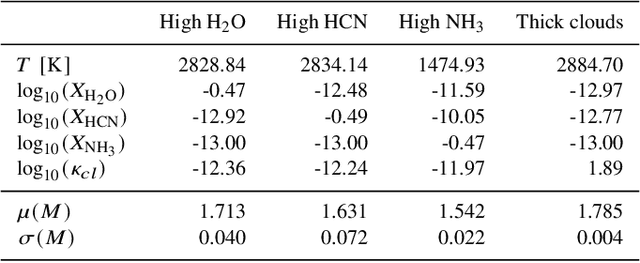
The physical characteristics and atmospheric chemical composition of newly discovered exoplanets are often inferred from their transit spectra which are obtained from complex numerical models of radiative transfer. Alternatively, simple analytical expressions provide insightful physical intuition into the relevant atmospheric processes. The deep learning revolution has opened the door for deriving such analytical results directly with a computer algorithm fitting to the data. As a proof of concept, we successfully demonstrate the use of symbolic regression on synthetic data for the transit radii of generic hot Jupiter exoplanets to derive a corresponding analytical formula. As a preprocessing step, we use dimensional analysis to identify the relevant dimensionless combinations of variables and reduce the number of independent inputs, which improves the performance of the symbolic regression. The dimensional analysis also allowed us to mathematically derive and properly parametrize the most general family of degeneracies among the input atmospheric parameters which affect the characterization of an exoplanet atmosphere through transit spectroscopy.