Is the Machine Smarter than the Theorist: Deriving Formulas for Particle Kinematics with Symbolic Regression
Paper and Code
Nov 15, 2022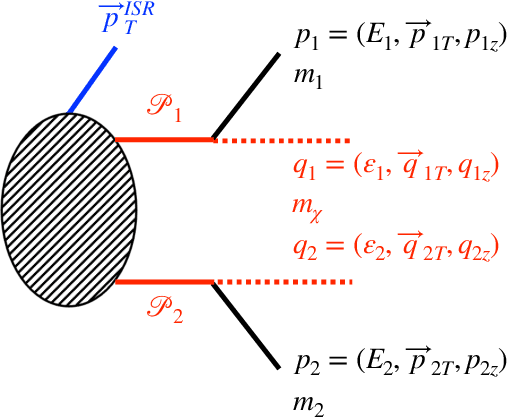
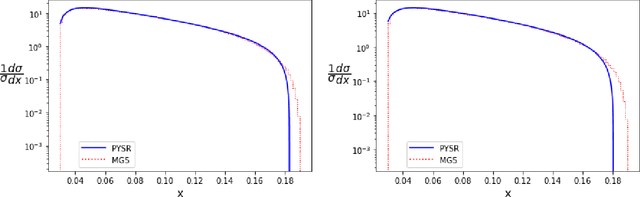
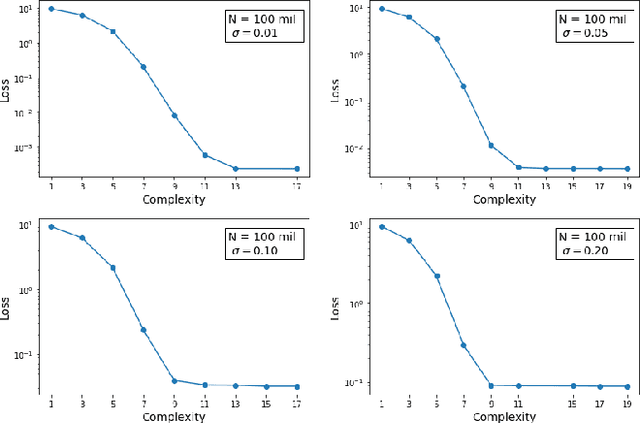
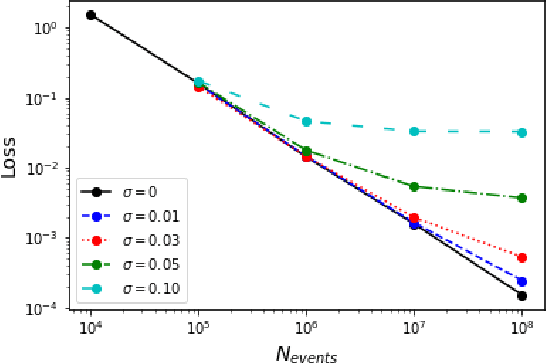
We demonstrate the use of symbolic regression in deriving analytical formulas, which are needed at various stages of a typical experimental analysis in collider phenomenology. As a first application, we consider kinematic variables like the stransverse mass, $M_{T2}$, which are defined algorithmically through an optimization procedure and not in terms of an analytical formula. We then train a symbolic regression and obtain the correct analytical expressions for all known special cases of $M_{T2}$ in the literature. As a second application, we reproduce the correct analytical expression for a next-to-leading order (NLO) kinematic distribution from data, which is simulated with a NLO event generator. Finally, we derive analytical approximations for the NLO kinematic distributions after detector simulation, for which no known analytical formulas currently exist.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge