New Machine Learning Techniques for Simulation-Based Inference: InferoStatic Nets, Kernel Score Estimation, and Kernel Likelihood Ratio Estimation

We propose an intuitive, machine-learning approach to multiparameter inference, dubbed the InferoStatic Networks (ISN) method, to model the score and likelihood ratio estimators in cases when the probability density can be sampled but not computed directly. The ISN uses a backend neural network that models a scalar function called the inferostatic potential $\varphi$. In addition, we introduce new strategies, respectively called Kernel Score Estimation (KSE) and Kernel Likelihood Ratio Estimation (KLRE), to learn the score and the likelihood ratio functions from simulated data. We illustrate the new techniques with some toy examples and compare to existing approaches in the literature. We mention en passant some new loss functions that optimally incorporate latent information from simulations into the training procedure.

Deep-Learned Event Variables for Collider Phenomenology

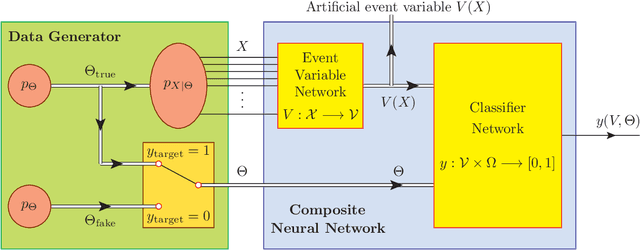
The choice of optimal event variables is crucial for achieving the maximal sensitivity of experimental analyses. Over time, physicists have derived suitable kinematic variables for many typical event topologies in collider physics. Here we introduce a deep learning technique to design good event variables, which are sensitive over a wide range of values for the unknown model parameters. We demonstrate that the neural networks trained with our technique on some simple event topologies are able to reproduce standard event variables like invariant mass, transverse mass, and stransverse mass. The method is automatable, completely general, and can be used to derive sensitive, previously unknown, event variables for other, more complex event topologies.

InClass Nets: Independent Classifier Networks for Nonparametric Estimation of Conditional Independence Mixture Models and Unsupervised Classification

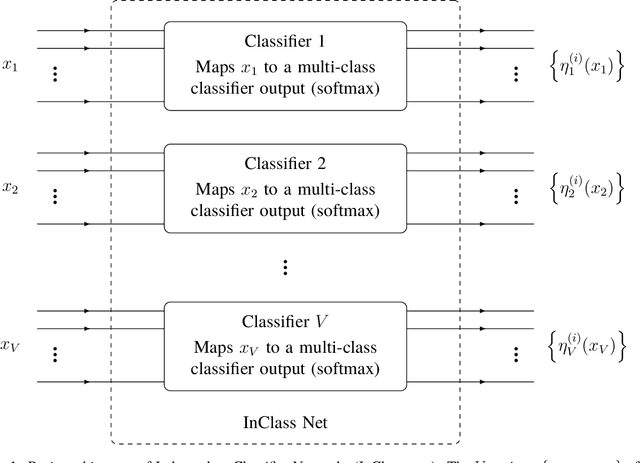
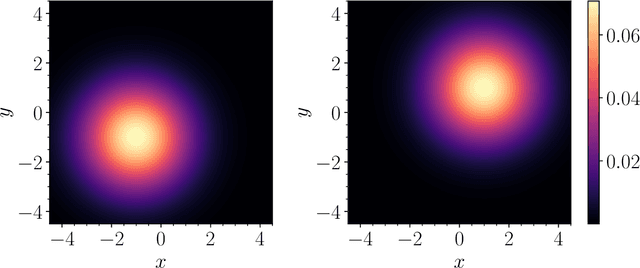
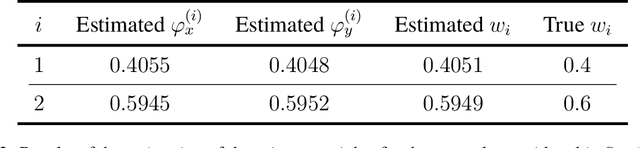
We introduce a new machine-learning-based approach, which we call the Independent Classifier networks (InClass nets) technique, for the nonparameteric estimation of conditional independence mixture models (CIMMs). We approach the estimation of a CIMM as a multi-class classification problem, since dividing the dataset into different categories naturally leads to the estimation of the mixture model. InClass nets consist of multiple independent classifier neural networks (NNs), each of which handles one of the variates of the CIMM. Fitting the CIMM to the data is performed by simultaneously training the individual NNs using suitable cost functions. The ability of NNs to approximate arbitrary functions makes our technique nonparametric. Further leveraging the power of NNs, we allow the conditionally independent variates of the model to be individually high-dimensional, which is the main advantage of our technique over existing non-machine-learning-based approaches. We derive some new results on the nonparametric identifiability of bivariate CIMMs, in the form of a necessary and a (different) sufficient condition for a bivariate CIMM to be identifiable. We provide a public implementation of InClass nets as a Python package called RainDancesVI and validate our InClass nets technique with several worked out examples. Our method also has applications in unsupervised and semi-supervised classification problems.