Simple initialization and parametrization of sinusoidal networks via their kernel bandwidth

Neural networks with sinusoidal activations have been proposed as an alternative to networks with traditional activation functions. Despite their promise, particularly for learning implicit models, their training behavior is not yet fully understood, leading to a number of empirical design choices that are not well justified. In this work, we first propose a simplified version of such sinusoidal neural networks, which allows both for easier practical implementation and simpler theoretical analysis. We then analyze the behavior of these networks from the neural tangent kernel perspective and demonstrate that their kernel approximates a low-pass filter with an adjustable bandwidth. Finally, we utilize these insights to inform the sinusoidal network initialization, optimizing their performance for each of a series of tasks, including learning implicit models and solving differential equations.

HyperPINN: Learning parameterized differential equations with physics-informed hypernetworks

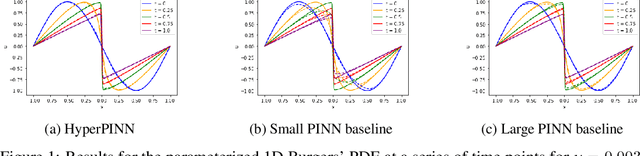
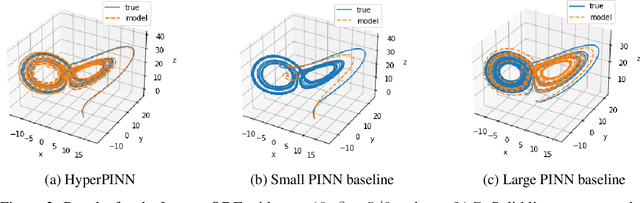
Many types of physics-informed neural network models have been proposed in recent years as approaches for learning solutions to differential equations. When a particular task requires solving a differential equation at multiple parameterizations, this requires either re-training the model, or expanding its representation capacity to include the parameterization -- both solution that increase its computational cost. We propose the HyperPINN, which uses hypernetworks to learn to generate neural networks that can solve a differential equation from a given parameterization. We demonstrate with experiments on both a PDE and an ODE that this type of model can lead to neural network solutions to differential equations that maintain a small size, even when learning a family of solutions over a parameter space.

Combining Differentiable PDE Solvers and Graph Neural Networks for Fluid Flow Prediction

Solving large complex partial differential equations (PDEs), such as those that arise in computational fluid dynamics (CFD), is a computationally expensive process. This has motivated the use of deep learning approaches to approximate the PDE solutions, yet the simulation results predicted from these approaches typically do not generalize well to truly novel scenarios. In this work, we develop a hybrid (graph) neural network that combines a traditional graph convolutional network with an embedded differentiable fluid dynamics simulator inside the network itself. By combining an actual CFD simulator (run on a much coarser resolution representation of the problem) with the graph network, we show that we can both generalize well to new situations and benefit from the substantial speedup of neural network CFD predictions, while also substantially outperforming the coarse CFD simulation alone.