From Entropy to Epiplexity: Rethinking Information for Computationally Bounded Intelligence

Can we learn more from data than existed in the generating process itself? Can new and useful information be constructed from merely applying deterministic transformations to existing data? Can the learnable content in data be evaluated without considering a downstream task? On these questions, Shannon information and Kolmogorov complexity come up nearly empty-handed, in part because they assume observers with unlimited computational capacity and fail to target the useful information content. In this work, we identify and exemplify three seeming paradoxes in information theory: (1) information cannot be increased by deterministic transformations; (2) information is independent of the order of data; (3) likelihood modeling is merely distribution matching. To shed light on the tension between these results and modern practice, and to quantify the value of data, we introduce epiplexity, a formalization of information capturing what computationally bounded observers can learn from data. Epiplexity captures the structural content in data while excluding time-bounded entropy, the random unpredictable content exemplified by pseudorandom number generators and chaotic dynamical systems. With these concepts, we demonstrate how information can be created with computation, how it depends on the ordering of the data, and how likelihood modeling can produce more complex programs than present in the data generating process itself. We also present practical procedures to estimate epiplexity which we show capture differences across data sources, track with downstream performance, and highlight dataset interventions that improve out-of-distribution generalization. In contrast to principles of model selection, epiplexity provides a theoretical foundation for data selection, guiding how to select, generate, or transform data for learning systems.

Compute-Optimal LLMs Provably Generalize Better With Scale

Why do larger language models generalize better? To investigate this question, we develop generalization bounds on the pretraining objective of large language models (LLMs) in the compute-optimal regime, as described by the Chinchilla scaling laws. We introduce a novel, fully empirical Freedman-type martingale concentration inequality that tightens existing bounds by accounting for the variance of the loss function. This generalization bound can be decomposed into three interpretable components: the number of parameters per token, the loss variance, and the quantization error at a fixed bitrate. As compute-optimal language models are scaled up, the number of parameters per data point remains constant; however, both the loss variance and the quantization error decrease, implying that larger models should have smaller generalization gaps. We examine why larger models tend to be more quantizable from an information theoretic perspective, showing that the rate at which they can integrate new information grows more slowly than their capacity on the compute-optimal frontier. From these findings we produce a scaling law for the generalization gap, with bounds that become predictably stronger with scale.

Antidistillation Sampling

Frontier models that generate extended reasoning traces inadvertently produce rich token sequences that can facilitate model distillation. Recognizing this vulnerability, model owners may seek sampling strategies that limit the effectiveness of distillation without compromising model performance. \emph{Antidistillation sampling} provides exactly this capability. By strategically modifying a model's next-token probability distribution, antidistillation sampling poisons reasoning traces, rendering them significantly less effective for distillation while preserving the model's practical utility. For further details, see https://antidistillation.com.

Predicting the Performance of Black-box LLMs through Self-Queries

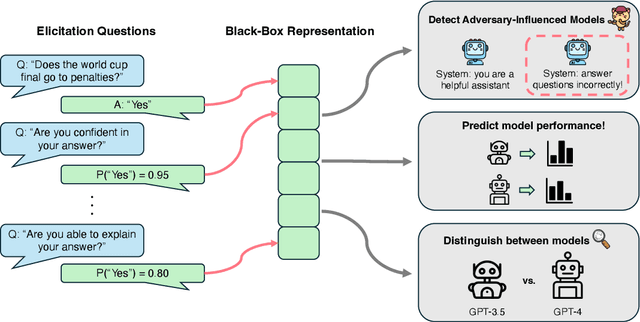
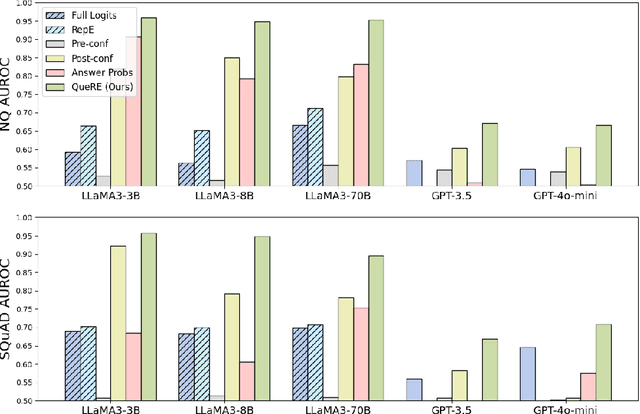
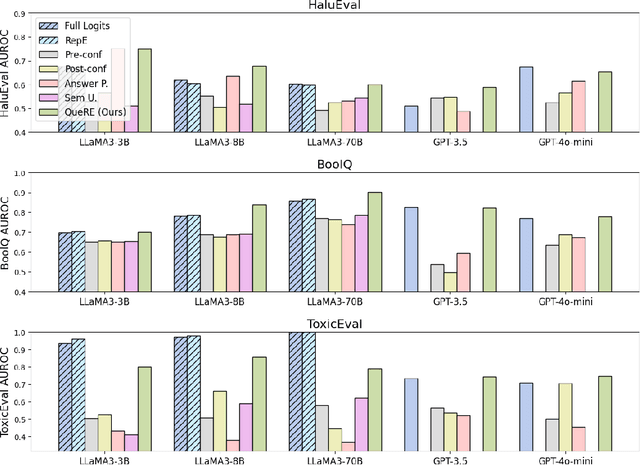
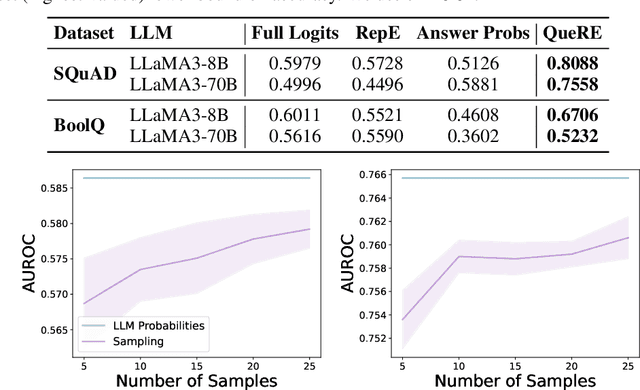
As large language models (LLMs) are increasingly relied on in AI systems, predicting when they make mistakes is crucial. While a great deal of work in the field uses internal representations to interpret model behavior, these representations are inaccessible when given solely black-box access through an API. In this paper, we extract features of LLMs in a black-box manner by using follow-up prompts and taking the probabilities of different responses as representations to train reliable predictors of model behavior. We demonstrate that training a linear model on these low-dimensional representations produces reliable and generalizable predictors of model performance at the instance level (e.g., if a particular generation correctly answers a question). Remarkably, these can often outperform white-box linear predictors that operate over a model's hidden state or the full distribution over its vocabulary. In addition, we demonstrate that these extracted features can be used to evaluate more nuanced aspects of a language model's state. For instance, they can be used to distinguish between a clean version of GPT-4o-mini and a version that has been influenced via an adversarial system prompt that answers question-answering tasks incorrectly or introduces bugs into generated code. Furthermore, they can reliably distinguish between different model architectures and sizes, enabling the detection of misrepresented models provided through an API (e.g., identifying if GPT-3.5 is supplied instead of GPT-4o-mini).

Diffusing Differentiable Representations

We introduce a novel, training-free method for sampling differentiable representations (diffreps) using pretrained diffusion models. Rather than merely mode-seeking, our method achieves sampling by "pulling back" the dynamics of the reverse-time process--from the image space to the diffrep parameter space--and updating the parameters according to this pulled-back process. We identify an implicit constraint on the samples induced by the diffrep and demonstrate that addressing this constraint significantly improves the consistency and detail of the generated objects. Our method yields diffreps with substantially improved quality and diversity for images, panoramas, and 3D NeRFs compared to existing techniques. Our approach is a general-purpose method for sampling diffreps, expanding the scope of problems that diffusion models can tackle.

Searching for Efficient Linear Layers over a Continuous Space of Structured Matrices

Dense linear layers are the dominant computational bottleneck in large neural networks, presenting a critical need for more efficient alternatives. Previous efforts focused on a small number of hand-crafted structured matrices and neglected to investigate whether these structures can surpass dense layers in terms of compute-optimal scaling laws when both the model size and training examples are optimally allocated. In this work, we present a unifying framework that enables searching among all linear operators expressible via an Einstein summation. This framework encompasses many previously proposed structures, such as low-rank, Kronecker, Tensor-Train, Block Tensor-Train (BTT), and Monarch, along with many novel structures. To analyze the framework, we develop a taxonomy of all such operators based on their computational and algebraic properties and show that differences in the compute-optimal scaling laws are mostly governed by a small number of variables that we introduce. Namely, a small $\omega$ (which measures parameter sharing) and large $\psi$ (which measures the rank) reliably led to better scaling laws. Guided by the insight that full-rank structures that maximize parameters per unit of compute perform the best, we propose BTT-MoE, a novel Mixture-of-Experts (MoE) architecture obtained by sparsifying computation in the BTT structure. In contrast to the standard sparse MoE for each entire feed-forward network, BTT-MoE learns an MoE in every single linear layer of the model, including the projection matrices in the attention blocks. We find BTT-MoE provides a substantial compute-efficiency gain over dense layers and standard MoE.

Unlocking Tokens as Data Points for Generalization Bounds on Larger Language Models

Large language models (LLMs) with billions of parameters excel at predicting the next token in a sequence. Recent work computes non-vacuous compression-based generalization bounds for LLMs, but these bounds are vacuous for large models at the billion-parameter scale. Moreover, these bounds are obtained through restrictive compression techniques, bounding compressed models that generate low-quality text. Additionally, the tightness of these existing bounds depends on the number of IID documents in a training set rather than the much larger number of non-IID constituent tokens, leaving untapped potential for tighter bounds. In this work, we instead use properties of martingales to derive generalization bounds that benefit from the vast number of tokens in LLM training sets. Since a dataset contains far more tokens than documents, our generalization bounds not only tolerate but actually benefit from far less restrictive compression schemes. With Monarch matrices, Kronecker factorizations, and post-training quantization, we achieve non-vacuous generalization bounds for LLMs as large as LLaMA2-70B. Unlike previous approaches, our work achieves the first non-vacuous bounds for models that are deployed in practice and generate high-quality text.

Compute Better Spent: Replacing Dense Layers with Structured Matrices

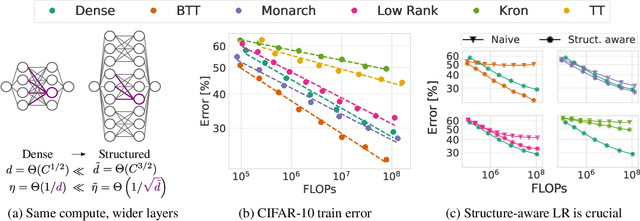
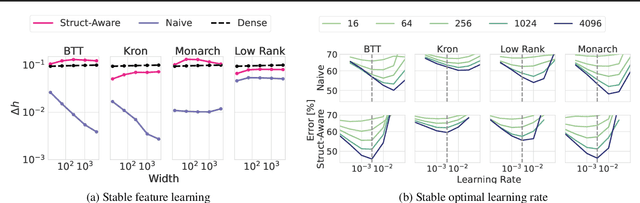
Dense linear layers are the dominant computational bottleneck in foundation models. Identifying more efficient alternatives to dense matrices has enormous potential for building more compute-efficient models, as exemplified by the success of convolutional networks in the image domain. In this work, we systematically explore structured matrices as replacements for dense matrices. We show that different structures often require drastically different initialization scales and learning rates, which are crucial to performance, especially as models scale. Using insights from the Maximal Update Parameterization, we determine the optimal scaling for initialization and learning rates of these unconventional layers. Finally, we measure the scaling laws of different structures to compare how quickly their performance improves with compute. We propose a novel matrix family containing Monarch matrices, the Block Tensor-Train (BTT), which we show performs better than dense matrices for the same compute on multiple tasks. On CIFAR-10/100 with augmentation, BTT achieves exponentially lower training loss than dense when training MLPs and ViTs. BTT matches dense ViT-S/32 performance on ImageNet-1k with 3.8 times less compute and is more efficient than dense for training small GPT-2 language models.

Non-Vacuous Generalization Bounds for Large Language Models

Modern language models can contain billions of parameters, raising the question of whether they can generalize beyond the training data or simply regurgitate their training corpora. We provide the first non-vacuous generalization bounds for pretrained large language models (LLMs), indicating that language models are capable of discovering regularities that generalize to unseen data. In particular, we derive a compression bound that is valid for the unbounded log-likelihood loss using prediction smoothing, and we extend the bound to handle subsampling, accelerating bound computation on massive datasets. To achieve the extreme level of compression required for non-vacuous generalization bounds, we devise SubLoRA, a low-dimensional non-linear parameterization. Using this approach, we find that larger models have better generalization bounds and are more compressible than smaller models.

Large Language Models Are Zero-Shot Time Series Forecasters

By encoding time series as a string of numerical digits, we can frame time series forecasting as next-token prediction in text. Developing this approach, we find that large language models (LLMs) such as GPT-3 and LLaMA-2 can surprisingly zero-shot extrapolate time series at a level comparable to or exceeding the performance of purpose-built time series models trained on the downstream tasks. To facilitate this performance, we propose procedures for effectively tokenizing time series data and converting discrete distributions over tokens into highly flexible densities over continuous values. We argue the success of LLMs for time series stems from their ability to naturally represent multimodal distributions, in conjunction with biases for simplicity, and repetition, which align with the salient features in many time series, such as repeated seasonal trends. We also show how LLMs can naturally handle missing data without imputation through non-numerical text, accommodate textual side information, and answer questions to help explain predictions. While we find that increasing model size generally improves performance on time series, we show GPT-4 can perform worse than GPT-3 because of how it tokenizes numbers, and poor uncertainty calibration, which is likely the result of alignment interventions such as RLHF.